6.8 直流法潮流计算

1、实验目的

潮流计算是电力系统中非常重要的分析计算，指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下，计算有功功率、无功功率及电压在电力网中的分布。而直流法潮流计算是一种基于线性模型的简化潮流算法。

从数学上看，直流法潮流计算（DCPF）是求解一组由潮流方程描述的线性代数方程组。通过该应用案例，展示低代码控制器线性方程(Solve动作)求解功能。

2、实验原理

对于一个N节点电网，经过适当假设可得到直流法潮流方程（矩阵形式）：P=Bθ。式中矩阵表示如下：

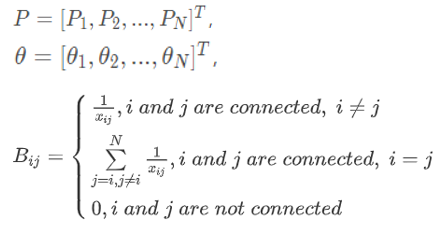
直流法潮流方程

其中有功功率P、电纳矩阵B为已知量，待计算值为各节点电压相角。

3、实验步骤

本直流法潮流计算的对象选取为matpower中的case5标准算例。具体步骤如下

3.1、测点配置

测点配置表格的内容包含了测点的点号、名称、别名、是否离散、是否是计算点以及默认值等。点号是程序里给这个测点的编号，可以自己定义，使用时，测点与通信通道的点号一一对应完成对接。别名是英文字母与下划线组合使用，可以当做变量名用于AOE表格里表达式的书写，使之可以不用点号来表达，使得表达式的意思表达得更加清楚。本案例测点配置如下：

序号点号名称别名是否离散是否计算点默认值备注
1100001测点1DoCal_POINTTRUEFALSE0计算控制
2100002测点2theta1FALSEFALSE0节点1电压相角
3100003测点3theta2FALSEFALSE0节点2电压相角
4100004测点4theta3FALSEFALSE0节点3电压相角
5100005测点5theta4FALSEFALSE0节点4电压相角
6100006测点6theta5FALSEFALSE0节点5电压相角

3.2、AOE配置

本案例中AOE文件配置内容分为三个部分。

AOE网络声明

名称为直流法潮流计算，触发条件设置为事件驱动（Event_Drive）。

AOE ID是否启用名称触发条件触发条件参数变量初始值
70001TRUE直流法潮流计算Event_Drivex1:0;x2:0;x3:0;x4:0;x5:0;

AOE节点声明

AOE ID节点ID名称节点类型超时时间(ms)表达式
700011开始节点Condition10DoCal_POINT > 0.5
700012计算节点Condition101
700013幅值Condition101
700014结束节点Condition10DoCal_POINT == 0

本案例中共有4个节点，节点类型均为Condition，表达式设为1，表明始终满足条件触发执行。

AOE边声明

AOE ID首尾节点动作名称失败模式动作类型动作参数
700011;2进入直流潮流计算DefaultSet_PointsDoCal_POINT:0;
700012;3计算直流潮流DefaultSolve+224.7319x1-35.5872x2-32.8947x4-156.25x5=2.1;
-35.5872x1+128.1798x2-92.5926x3=-3;
-92.5926x2+126.2626x3-33.67x4=0.2349;
x4=0;
-156.25x1-33.67x4+189.92*x5=4.6651;
x1,x2,x3,x4,x5
700013;4赋值DefaultSet_Pointstheta1:x1;
theta2:x2;
theta3:x3;
theta4:0;
theta5:x5;

4、运行计算

将上述配置文件上传至低代码控制器中，运行即可得到计算结果，其运算结果如下所示。

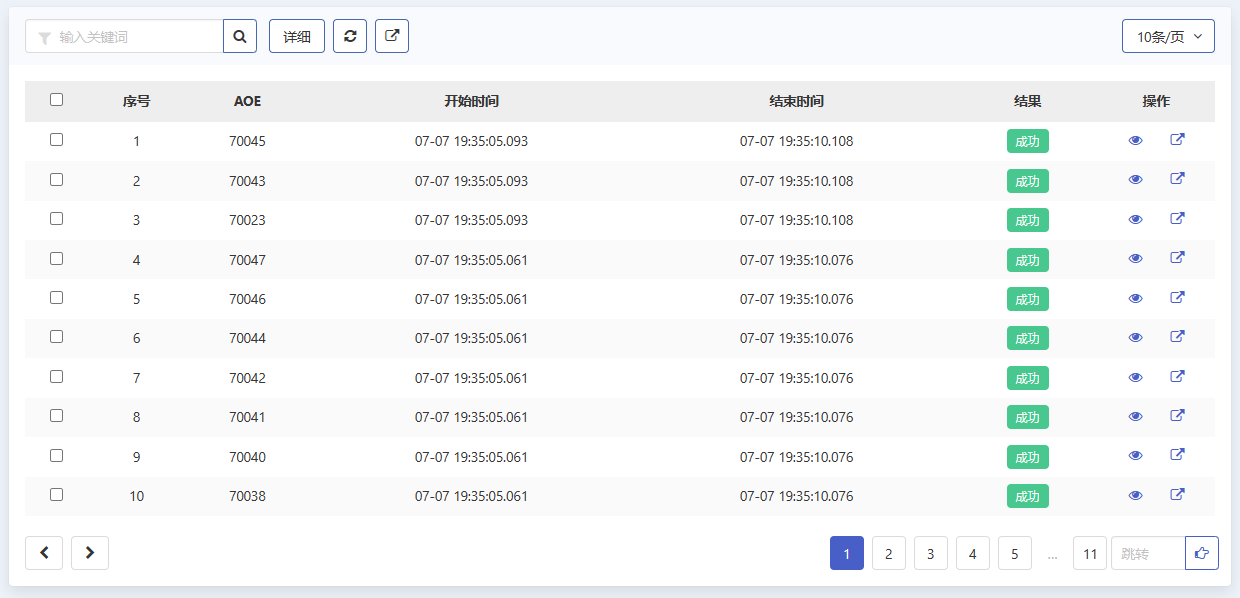
直流潮流计算结果

matpower计算结果如下：

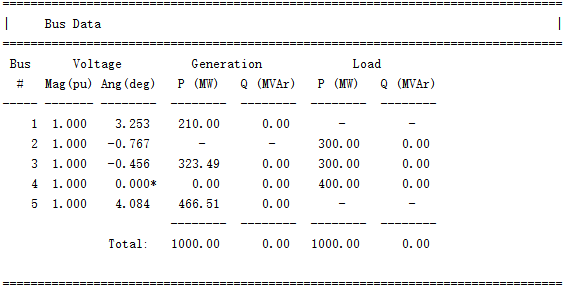
matpower直流潮流计算结果

对比低代码控制器与matpower计算结果，可见低代码控制器对于直流法潮流能够精确计算。

附件：直流法潮流计算.rar