6.10 最优潮流计算
1、实验目的
最优潮流(Optimal Power Flow,OPF)是指当系统的结构参数和负荷情况都已给定时,调节可利用的控制变量(如发电机输出功率、可调变压器抽头等)来找到能满足所有运行约束条件的,并使系统的某一性能指标(如发电成本或网络损耗)达到最优值下的潮流分布。
从数学上看,最优潮流计算是一个典型的非线性优化问题。通过该应用案例,展示低代码控制器非线性规划(NLP动作)求解功能。
2、实验原理
最优潮流的数学模型如下所示:
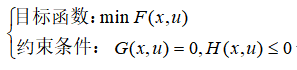
式中,F为目标函数;G为等式约束条件;H为不等式约束条件;x为状态变量,u为控制变量。
最优潮流的目标函数类型很多,常见为以下2种:
(1)系统运行成本最小,一般表示为火电机组燃料费用最小(不考虑启动、停机费用)。
(2)有功传输损耗最小,通常以有功传输最小为目标.
最优潮流考虑的系统约束条件有: (1)各节点有功功率和无功功率的平衡约束。 (2)各发电机有功出力上下界约束。 (3)各发电机、同步补偿机无功出力上下界约束。 (4)并联电抗器、电容器容量约束。 (5)移相器抽头位置约束。 (6)可调变压器抽头位置约束。 (7)各节点电压幅值上下界约束。 (8)各支路传输功率约束。
3、实验步骤
本最优潮流计算的对象选取为matpower中的case9标准算例,目标函数为系统运行成本最小(即发电机组有功出力最小)。具体步骤如下
3.1、测点配置
测点配置表格的内容包含了测点的点号、名称、别名、是否离散、是否是计算点以及默认值等。点号是程序里给这个测点的编号,可以自己定义,使用时,测点与通信通道的点号一一对应完成对接。别名是英文字母与下划线组合使用,可以当做变量名用于AOE表格里表达式的书写,使之可以不用点号来表达,使得表达式的意思表达得更加清楚。本案例测点配置如下:
| 序号 | 点号 | 名称 | 别名 | 是否离散 | 是否计算点 | 默认值 | 备注 |
|---|---|---|---|---|---|---|---|
| 1 | 100001 | 测点1 | DoCal_POINT | TRUE | FALSE | 0 | 计算控制 |
| 2 | 100002 | 测点2 | V1 | FALSE | FALSE | 1 | 节点1电压幅值 |
| 3 | 100003 | 测点3 | V2 | FALSE | FALSE | 1 | 节点2电压幅值 |
| 4 | 100004 | 测点4 | V3 | FALSE | FALSE | 1 | 节点3电压幅值 |
| 5 | 100005 | 测点5 | V4 | FALSE | FALSE | 1 | 节点4电压幅值 |
| 6 | 100006 | 测点6 | V5 | FALSE | FALSE | 1 | 节点5电压幅值 |
| 7 | 100007 | 测点7 | V6 | FALSE | FALSE | 1 | 节点6电压幅值 |
| 8 | 100008 | 测点8 | V7 | FALSE | FALSE | 1 | 节点7电压幅值 |
| 9 | 100009 | 测点9 | V8 | FALSE | FALSE | 1 | 节点8电压幅值 |
| 10 | 100010 | 测点10 | V9 | FALSE | FALSE | 1 | 节点9电压幅值 |
| 11 | 100011 | 测点11 | THETA1 | FALSE | FALSE | 0 | 节点1电压相角 |
| 12 | 100012 | 测点12 | THETA2 | FALSE | FALSE | 0 | 节点2电压相角 |
| 13 | 100013 | 测点13 | THETA3 | FALSE | FALSE | 0 | 节点3电压相角 |
| 14 | 100014 | 测点14 | THETA4 | FALSE | FALSE | 0 | 节点4电压相角 |
| 15 | 100015 | 测点15 | THETA5 | FALSE | FALSE | 0 | 节点5电压相角 |
| 16 | 100016 | 测点16 | THETA6 | FALSE | FALSE | 0 | 节点6电压相角 |
| 17 | 100017 | 测点17 | THETA7 | FALSE | FALSE | 0 | 节点7电压相角 |
| 18 | 100018 | 测点18 | THETA8 | FALSE | FALSE | 0 | 节点8电压相角 |
| 19 | 100019 | 测点19 | THETA9 | FALSE | FALSE | 0 | 节点9电压相角 |
| 20 | 100020 | 测点20 | PG1 | FALSE | FALSE | 0 | 发电机1有功输出 |
| 21 | 100021 | 测点21 | PG2 | FALSE | FALSE | 0 | 发电机2有功输出 |
| 22 | 100022 | 测点22 | PG3 | FALSE | FALSE | 0 | 发电机3有功输出 |
| 23 | 100023 | 测点23 | QG1 | FALSE | FALSE | 0 | 发电机1无功输出 |
| 24 | 100024 | 测点24 | QG2 | FALSE | FALSE | 0 | 发电机2无功输出 |
| 25 | 100025 | 测点25 | QG3 | FALSE | FALSE | 0 | 发电机3无功输出 |
3.2、AOE配置
本案例中AOE文件配置内容分为三个部分。
AOE网络声明
名称为最优潮流计算,触发条件设置为事件驱动(Event_Drive)。
| AOE ID | 是否启用 | 名称 | 触发条件 | 触发条件参数 | 变量初始值 |
|---|---|---|---|---|---|
| 70001 | TRUE | 最优潮流计算 | Event_Drive | V_1:1;V_2:1;V_3:1;V_4:1;V_5:1;V_6:1;V_7:1;V_8:1;V_9:1; THETA_1:0;THETA_2:0;THETA_3:0;THETA_4:0;THETA_5:0;THETA_6:0;THETA_7:0;THETA_8:0;THETA_9:0; PG_1:0;PG_2:0;PG_3:0; QG_1:0;QG_2:0;QG_3:0; |
AOE节点声明
| AOE ID | 节点ID | 名称 | 节点类型 | 超时时间(ms) | 表达式 |
|---|---|---|---|---|---|
| 70001 | 1 | 开始节点 | Condition | 10 | DoCal_POINT > 0.5 |
| 70001 | 2 | 计算节点 | Condition | 10 | 1 |
| 70001 | 3 | 幅值 | Condition | 10 | 1 |
| 70001 | 4 | 结束节点 | Condition | 10 | DoCal_POINT == 0 |
本案例中共有4个节点,节点类型均为Condition,表达式设为1,表明始终满足条件触发执行。
AOE边声明
| AOE ID | 首尾节点 | 动作名称 | 失败模式 | 动作类型 | 动作参数 | |
|---|---|---|---|---|---|---|
| 70001 | 1;2 | 进入最优潮流计算 | Default | Set_Points | DoCal_POINT:0; | |
| 70001 | 2;3 | 最优潮流计算 | Default | NLP | 100.0PG_2(8.5PG_2 + 1.2) + 100.0PG_3*(12.25PG_3 + 1.0) + 100.0PG_1*(11.0PG_1 + 5.0) + 1085.0; 17.361111111111111111111111111111V_1V_4sin(THETA_1 -THETA_4) -PG_1:[0.00000000/0.00000000]; 16.0V_2V_8sin(THETA_2 -THETA_8) -PG_2:[0.00000000/0.00000000]; 17.064846416382252559726962457338V_3V_6sin(THETA_3 -THETA_6) -PG_3:[0.00000000/0.00000000]; 3.307378962025306456951057043625V_4^2 -V_4V_9*(1.365187713310580204778156996587cos(THETA_4 -THETA_9) - 11.60409556313993174061433447099sin(THETA_4 -THETA_9)) -V_4V_5(1.9421912487147263795270193076659cos(THETA_4 -THETA_5) - 10.510682051867930995087398606192sin(THETA_4 -THETA_5)) - 17.361111111111111111111111111111V_1V_4sin(THETA_1 -THETA_4):[0.00000000/0.00000000]; 3.2242003871388416058607617742382V_5^2 -V_4V_5(1.9421912487147263795270193076659cos(THETA_4 -THETA_5) + 10.510682051867930995087398606192sin(THETA_4 -THETA_5)) -V_5V_6(1.282009138424114920614049505276cos(THETA_5 -THETA_6) - 5.588244962361526013694401626708sin(THETA_5 -THETA_6)) + 0.9:[0.00000000/0.00000000]; 2.4370966193142118427772402355913V_6^2 - 17.064846416382252559726962457338V_3V_6sin(THETA_3 -THETA_6) -V_6V_7(1.1550874808900968235094275522337cos(THETA_6 -THETA_7) - 9.784270426363173093256327501274sin(THETA_6 -THETA_7)) -V_5V_6(1.282009138424114920614049505276cos(THETA_5 -THETA_6) + 5.588244962361526013694401626708sin(THETA_5 -THETA_6)):[0.00000000/0.00000000]; 2.772209954136232376422626125361V_7^2 -V_7V_8*(1.6171224732461355529131985731272cos(THETA_7 -THETA_8) - 13.697978596908442330558858501784sin(THETA_7 -THETA_8)) -V_6V_7(1.1550874808900968235094275522337cos(THETA_6 -THETA_7) + 9.784270426363173093256327501274sin(THETA_6 -THETA_7)) + 1.0:[0.00000000/0.00000000]; 2.8047268525372843761545027518878V_8^2 -V_7V_8*(1.6171224732461355529131985731272cos(THETA_7 -THETA_8) + 13.697978596908442330558858501784sin(THETA_7 -THETA_8)) - 16.0V_2V_8sin(THETA_2 -THETA_8) -V_8V_9*(1.1876043792911486361105956578215cos(THETA_8 -THETA_9) - 5.9751345333085915754314344034144sin(THETA_8 -THETA_9)):[0.00000000/0.00000000]; 2.5527920926017282354791859688703V_9^2 -V_4V_9*(1.365187713310580204778156996587cos(THETA_4 -THETA_9) + 11.60409556313993174061433447099sin(THETA_4 -THETA_9)) -V_8V_9(1.1876043792911486361105956578215cos(THETA_8 -THETA_9) + 5.9751345333085915754314344034144sin(THETA_8 -THETA_9)) + 1.25:[0.00000000/0.00000000]; 17.361111111111111111111111111111V_1^2 -QG_1 - 17.361111111111111111111111111111V_1V_4cos(THETA_1 -THETA_4):[0.00000000/0.00000000]; 16.0V_2^2 -QG_2 - 16.0V_2V_8cos(THETA_2 -THETA_8):[0.00000000/0.00000000]; 17.064846416382252559726962457338V_3^2 -QG_3 - 17.064846416382252559726962457338V_3V_6cos(THETA_3 -THETA_6):[0.00000000/0.00000000]; 39.308888726118972556378139415756V_4^2 -V_4V_9*(11.60409556313993174061433447099cos(THETA_4 -THETA_9) + 1.365187713310580204778156996587sin(THETA_4 -THETA_9)) - 17.361111111111111111111111111111V_1V_4cos(THETA_1 -THETA_4) -V_4V_5*(10.510682051867930995087398606192cos(THETA_4 -THETA_5) + 1.9421912487147263795270193076659sin(THETA_4 -THETA_5)):[0.00000000/0.00000000]; 15.840927014229457370220188749954V_5^2 -V_4V_5*(10.510682051867930995087398606192cos(THETA_4 -THETA_5) - 1.9421912487147263795270193076659sin(THETA_4 -THETA_5)) -V_5V_6(5.588244962361526013694401626708cos(THETA_5 -THETA_6) + 1.282009138424114920614049505276sin(THETA_5 -THETA_6)) + 0.3:[0.00000000/0.00000000]; 32.15386180510695623979700030759V_6^2 - 17.064846416382252559726962457338V_3V_6cos(THETA_3 -THETA_6) -V_6V_7(9.784270426363173093256327501274cos(THETA_6 -THETA_7) + 1.1550874808900968235094275522337sin(THETA_6 -THETA_7)) -V_5V_6(5.588244962361526013694401626708cos(THETA_5 -THETA_6) - 1.282009138424114920614049505276sin(THETA_5 -THETA_6)):[0.00000000/0.00000000]; 23.303249023271618511898850556463V_7^2 -V_7V_8*(13.697978596908442330558858501784cos(THETA_7 -THETA_8) + 1.6171224732461355529131985731272sin(THETA_7 -THETA_8)) -V_6V_7(9.784270426363173093256327501274cos(THETA_6 -THETA_7) - 1.1550874808900968235094275522337sin(THETA_6 -THETA_7)) + 0.35:[0.00000000/0.00000000]; 35.445613130217033415192418033257V_8^2 - 16.0V_2V_8cos(THETA_2 -THETA_8) -V_7V_8(13.697978596908442330558858501784cos(THETA_7 -THETA_8) - 1.6171224732461355529131985731272sin(THETA_7 -THETA_8)) -V_8V_9(5.9751345333085915754314344034144cos(THETA_8 -THETA_9) + 1.1876043792911486361105956578215sin(THETA_8 -THETA_9)):[0.00000000/0.00000000]; 17.33823009644852319866004108917V_9^2 -V_4V_9*(11.60409556313993174061433447099cos(THETA_4 -THETA_9) - 1.365187713310580204778156996587sin(THETA_4 -THETA_9)) -V_8V_9(5.9751345333085915754314344034144cos(THETA_8 -THETA_9) - 1.1876043792911486361105956578215sin(THETA_8 -THETA_9)) + 0.5:[0.00000000/0.00000000]; 17.361111111111111111111111111111V_1V_4sin(THETA_1 -THETA_4):[/2.50000000]; -17.361111111111111111111111111111V_1V_4sin(THETA_1 -THETA_4):[/2.50000000]; 1.9421912487147263795270193076659V_4^2 -V_4V_5*(1.9421912487147263795270193076659cos(THETA_4 -THETA_5) - 10.510682051867930995087398606192sin(THETA_4 -THETA_5)):[/2.50000000]; 1.9421912487147263795270193076659V_5^2 -V_4V_5*(1.9421912487147263795270193076659cos(THETA_4 -THETA_5) + 10.510682051867930995087398606192sin(THETA_4 -THETA_5)):[/2.50000000]; 1.282009138424114920614049505276V_5^2 -V_5V_6*(1.282009138424114920614049505276cos(THETA_5 -THETA_6) - 5.588244962361526013694401626708sin(THETA_5 -THETA_6)):[/1.50000000]; 1.282009138424114920614049505276V_6^2 -V_5V_6*(1.282009138424114920614049505276cos(THETA_5 -THETA_6) + 5.588244962361526013694401626708sin(THETA_5 -THETA_6)):[/1.50000000]; 17.064846416382252559726962457338V_3V_6sin(THETA_3 -THETA_6):[/3.00000000]; -17.064846416382252559726962457338V_3V_6sin(THETA_3 -THETA_6):[/3.00000000]; 1.1550874808900968235094275522337V_6^2 -V_6V_7*(1.1550874808900968235094275522337cos(THETA_6 -THETA_7) - 9.784270426363173093256327501274sin(THETA_6 -THETA_7)):[/1.50000000]; 1.1550874808900968235094275522337V_7^2 -V_6V_7*(1.1550874808900968235094275522337cos(THETA_6 -THETA_7) + 9.784270426363173093256327501274sin(THETA_6 -THETA_7)):[/1.50000000]; 1.6171224732461355529131985731272V_7^2 -V_7V_8*(1.6171224732461355529131985731272cos(THETA_7 -THETA_8) - 13.697978596908442330558858501784sin(THETA_7 -THETA_8)):[/2.50000000]; 1.6171224732461355529131985731272V_8^2 -V_7V_8*(1.6171224732461355529131985731272cos(THETA_7 -THETA_8) + 13.697978596908442330558858501784sin(THETA_7 -THETA_8)):[/2.50000000]; -16.0V_2V_8sin(THETA_2 -THETA_8):[/2.50000000]; 16.0V_2V_8sin(THETA_2 -THETA_8):[/2.50000000]; 1.1876043792911486361105956578215V_8^2 -V_8V_9*(1.1876043792911486361105956578215cos(THETA_8 -THETA_9) - 5.9751345333085915754314344034144sin(THETA_8 -THETA_9)):[/2.50000000]; 1.1876043792911486361105956578215V_9^2 -V_8V_9*(1.1876043792911486361105956578215cos(THETA_8 -THETA_9) + 5.9751345333085915754314344034144sin(THETA_8 -THETA_9)):[/2.50000000]; 1.365187713310580204778156996587V_9^2 -V_4V_9*(1.365187713310580204778156996587cos(THETA_4 -THETA_9) + 11.60409556313993174061433447099sin(THETA_4 -THETA_9)):[/2.50000000]; 1.365187713310580204778156996587V_4^2 -V_4V_9*(1.365187713310580204778156996587cos(THETA_4 -THETA_9) - 11.60409556313993174061433447099sin(THETA_4 -THETA_9)):[/2.50000000]; THETA_1:[0.00000000/0.00000000]; PG_1:[0.10000000/2.50000000/],PG_2:[0.10000000/3.00000000/],PG_3:[0.10000000/2.70000000/],QG_1:[-3.00000000/3.00000000/],QG_2:[-3.00000000/3.00000000/],QG_3:[-3.00000000/3.00000000/],V_1:[0.90000000/1.10000000/],V_2:[0.90000000/1.10000000/],V_3:[0.90000000/1.10000000/],V_4:[0.90000000/1.10000000/],V_5:[0.90000000/1.10000000/],V_6:[0.90000000/1.10000000/],V_7:[0.90000000/1.10000000/],V_8:[0.90000000/1.10000000/],V_9:[0.90000000/1.10000000/],THETA_1:[//],THETA_2:[//],THETA_3:[//],THETA_4:[//],THETA_5:[//],THETA_6:[//],THETA_7:[//],THETA_8:[//],THETA_9:[//] | |
| 70001 | 3;4 | 赋值 | Default | Set_Points | V1:V_1; V2:V_2; V3:V_3; V4:V_4; V5:V_5; V6:V_6; V7:V_7; V8:V_8; V9:V_9; THETA1:THETA_1; THETA2:THETA_2; THETA3:THETA_3; THETA4:THETA_4; THETA5:THETA_5; THETA6:THETA_6; THETA7:THETA_7; THETA8:THETA_8; THETA9:THETA_9; PG1:PG_1; PG2:PG_2; PG3:PG_3; QG1:QG_1; QG2:QG_2; QG3:QG_3; |
4、运行计算
将上述配置文件上传至低代码控制器中,运行即可得到计算结果,其运算结果如下所示。
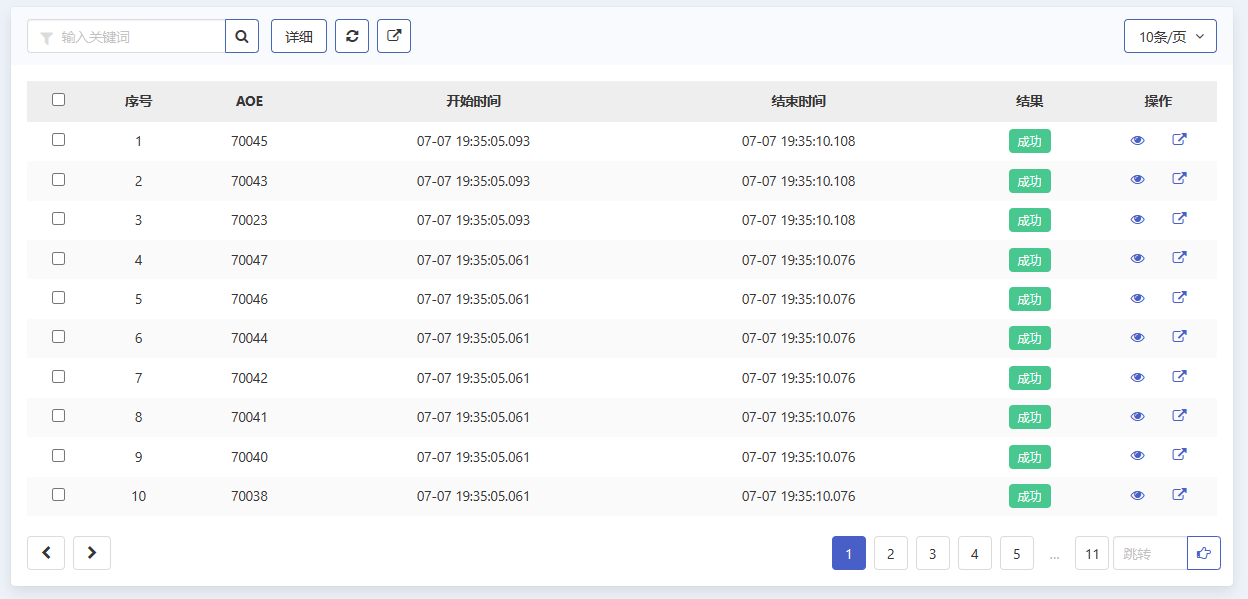
matpower计算结果如下:
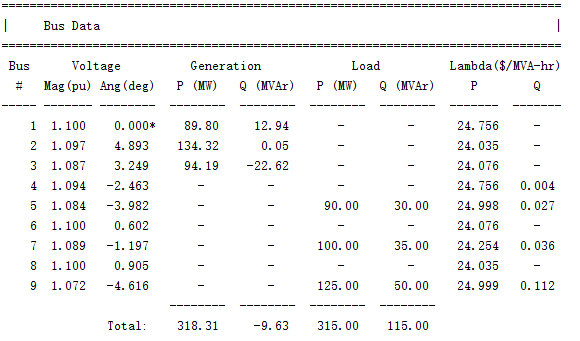
对比低代码控制器与matpower计算结果,可见低代码控制器对于交流法潮流能够精确计算(其中电压相角值的单位,低代码控制器为弧度,matpower为角度;低代码控制器的功率需乘以基准值100MW)。
附件:最优潮流计算.rar