EasySolve使用教程
EasySolve是由浙江大学SCOOL实验室开发的模型求解计算平台,模型输入简易,求解算法丰富,求解速度高效。
EasySolve是模型求解计算平台,您可以根据需要选择您的求解模式。本平台提供四种求解模式,分别是线性方程组求解(Ax=b)、非线性方程组求解(f(x)=0)、混合整数线性规划(MILP)、非线性规划(NLP)。
下面将按如下章节向大家介绍EasySolve的使用方法。
界面介绍
进入EasySolve模型求解计算平台后,其界面如下:
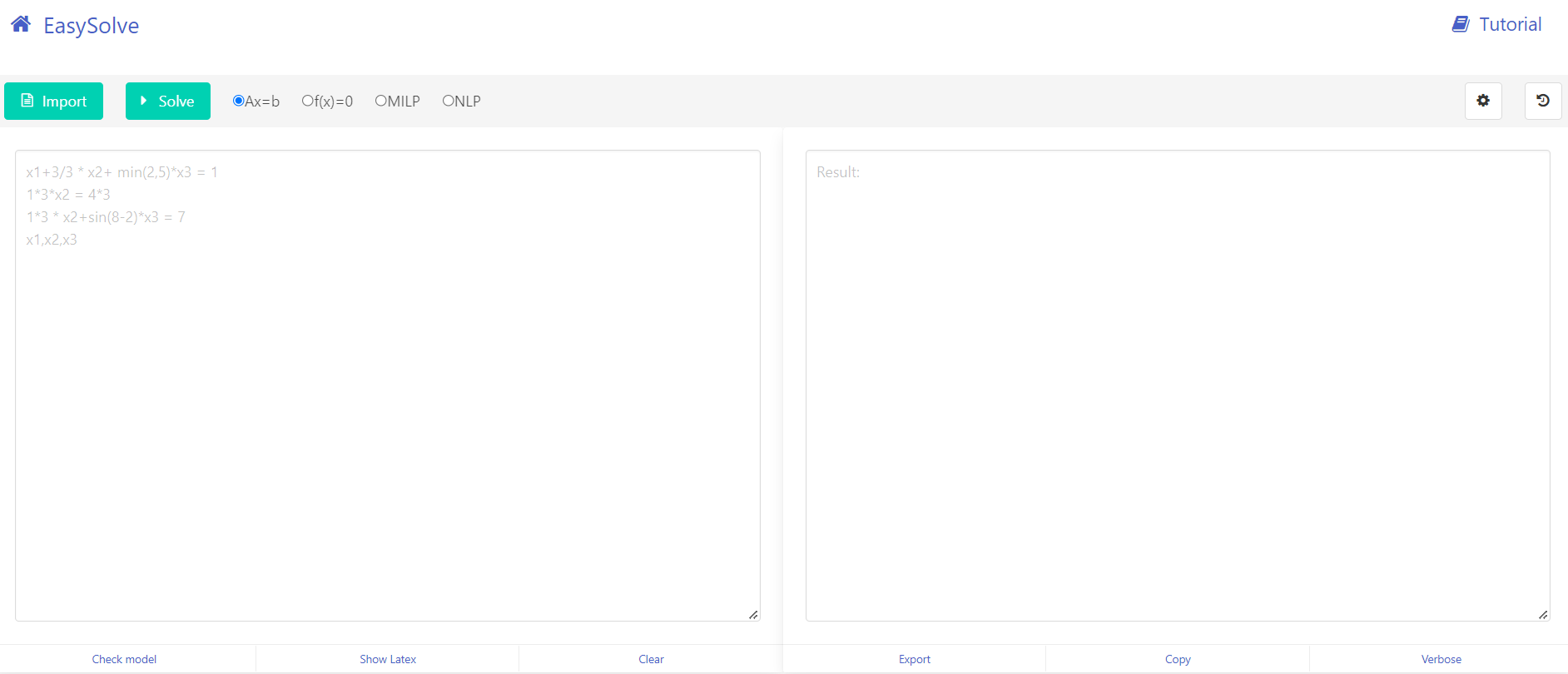
左侧工作框为求解内容,右侧框为结果输出。
您可以通过手动输入求解内容,也可以通过import自动上传求解模型。点击Clear可以清空输入窗口内容,重新进行书写。完成书写后,点击Solve,EasySolve会进行求解,并在右侧result页面输出结果。
您可以点击Check model查看数学表达式的属性以及变量情况;点击Show Latex显示Latex代码;点击Export输出结果,将生成一个excel表格存放结果;也可以选择Copy复制结果。您可以通过点击Verbose/Simple键切换结果显示的模式。
您可以在设置中更改设置,在右侧历史记录中查询历史版本。
基本语法
内置函数
EasySolve内置多种常用数学函数及实用时间获取函数,可通过向括号内传入参数进行直接调用,支持的函数及其具体功能如下表所示。
| 函数 | 功能 |
|---|---|
| abs() | 求绝对值 |
| sqrt() | 求平方根 |
| exp() | 求以e为底的指数 |
|ln()、log10()|求自然对数(以e为底)、求常用对数(以10为底)| |sin()、cos()、tan()|正弦函数、余弦函数、正切函数,单位为弧度| |asin()、acos()、atan()|反正弦函数、反余弦函数、反正切函数| |sinh()、cosh()、tanh()|双曲正弦函数、双曲余弦函数、双曲正切函数| |asinh()、acosh()、atanh()|反双曲正弦函数、反双曲余弦函数、反双曲正切函数|
|floor()|向下取整,即取不大于传入参数的最大整数| |ceil()|向上取整,即取不小于传入参数的最小整数| |round()|将传入参数进行四舍五入| |signum()|符号函数,指出参数正负号,若为正则返回1;零返回0;负返回-1| |max()、min()|求多个参数的最大值/最小值,参数用“,”分隔|
数字表示约定
EasySolve支持的将数字表示为科学计数法,如1e3,19e-2等。
EasySolve求解模式
按照求解模型的不同需求,EasySolve分成四种不同的求解模式。
| 求解模式 | 模式名称 | 含义 |
|---|---|---|
| Ax=b | 线性方程组求解 | 对非齐次线性方程组进行求解 |
| f(x)=0 | 非线性方程组求解 | 对齐次线性方程组进行求解 |
| MILP | 混合整数线性规划 | 混合整数线性规划问题求解 |
| NLP | 非线性规划 | 非线性规划问题求解 |
下面分节详细介绍各求解模式的具体内容和表达方式。
Ax=b(线性方程组求解)
可求解非齐次方程组 Ax = b,其中 A 为系数矩阵,x 为未知数组成的向量,b 为常数项向量。
在该模式下进行模型求解时,首先分行列写各方程,在最后一行列写所有变量,以**,**隔开。点击Solve,即可进行求解,在右侧result页面中输出结果。
#1)方程组:#
<方程式1>;
<方程式2>;
...
#2)变量声明:#
<变量名1>,<变量名2>,...
例:
x1+3/3*x3+min(2,5)*x3=1;
1*3*x2=4*3;
1*3*x2+sin(8-4)*x3=7;
x1,x2,x3
f(x)=0(非线性方程组求解)
可求解齐次方程组 f(x)=0,在书写方程组时只需写出左侧表达式,默认右侧为0。
书写方法与 Ax=b(非齐次方程组求解) 一致,先分行列写各方程,最后一行列写所有变量。点击Solve,即可进行求解,在右侧result页面中输出结果。
#1)方程组:#
<方程式1>;
<方程式2>;
...
#2)变量声明:#
<变量名1>,<变量名2>,...
注:为了使计算收敛,变量必要时需要赋初值,格式为<变量名:初值>;
例:
x1^2-10*x1+x2^2+8;
x1*x2^2+x1-10*x2+8;
x1,x2
MILP(混合整数线性规划)
用于在给定可行域内,求解线性约束下线性目标函数的最优解及最优值。
MILP全称为Mixed-integer linear programming,即混合整数线性规划,指目标函数和约束条件均为线性,部分决策变量限制为整数的数学规划问题。具体来说,其约束条件支持等式约束及不等式约束;变量类型包括 0-1变量、整型变量、实数型变量。
混合整数线性规划(MILP)的设置参数包括:
#1)目标函数:#
min/max(<表达式>);
#2)约束条件:#
<bool表达式1>;
<bool表达式2>;
...
#3)变量声明:#
<变量名1>:<变量类型1>,
<变量名2>:<变量类型2>,
...
其中变量类型包括以下三类:
| 变量类型 | 含义 |
|---|---|
| 1 | 0-1二进制变量 |
| 2 | 整型变量 |
| 3 | 实数型变量 |
实际列写时,按顺序写下目标函数、约束条件、变量声明的标准格式式子即可,上例中##间的备注内容不必写入。
注意一些写法:
- 约束,相等应当写作“==”。
- 最后一个变量结尾不加逗号。
- 分号用于区分目标函数和各条约束。如果不写分号,则需要严格换行,且变量需要写在一行里。
例1: 输入为:
max((5*1)*x1+3*x2+2*x3+(10-3)*x4+4*x5);
2*x1+(2*4)*x1+4*x3+2*x4+max(1,5)*x5<=5*2;
x1:1,x2:1,x3:1,x4:1,x5:1
输出为:
x1 : 0
x2 : 0.9999999999999999
x3 : 0
x4 : 1
x5 : 1
例2:输入为:
max(x+y)
x<=3
y<=2
x:3,y:3
输出为:
x : 3
y : 2
NLP(非线性规划)
此动作用于在给定可行域内,求解约束下目标函数的最优解及最优值,其中目标函数和约束条件至少有一个为非线性。
NLP全称为Nonlinear programming,即非线性规划,指目标函数和约束条件至少有一个为非线性的数学规划问题。具体来说,其约束条件支持等式约束及不等式约束;变量类型包括实数型变量。
#1)目标函数:#
<表达式>
#2)约束条件:#
<表达式1>:[表达式下限/表达式上限];
<表达式2>:[表达式下限/表达式上限];
...
#3)变量声明:#
<变量名1>:[变量下限/变量上限/初始值],
<变量名2>:[变量下限/变量上限/初始值],
...
注:
1.若无上下限对应位置不写,如x[/3]表示变量x≤3;
2.变量声明若无初始值要求,可简写为[变量下限/变量上限]。
例:
输入为:
x1*x4*(x1+x2+x3)+x3;
x1*x2*x3*x4:[25/2e19];
x1^2+x2^2+x3^2+x4^2:[40/40];
x1:[1/5],x2:[1/5],x3:[1/5],x4:[1/5],x5:[1/5]
输出为:
x1 : 0.9999999900104724
x2 : 4.742999643578167
x3 : 3.8211499789477092
x4 : 1.3794082932131775
x5 : 3.000000797771693