基于辅助因子两步求解算法的孤岛微电网潮流计算
本文发表于《电网技术》。通过方程变形与求解步骤改变,使孤岛微电网潮流计算变得更加鲁棒高效。
研究背景
微电网潮流计算作为微电网稳定分析、优化配置的基础,是一个重要的研究领域。并网运行的微电网存在一个根节点,其潮流计算与配电网潮流计算相似。而孤岛运行的微电网在对等控制下,系统内不存在平衡节点,需对系统频率进行求解,且线路阻抗比较高,潮流计算中牛拉法容易出现不收敛、雅克比矩阵奇异等问题,故传统的潮流计算方法不再适用。本文提出的辅助因子两步求解算法具有鲁棒性强的特点,一定程度上可以弥补牛拉法的不足。
辅助因子两步求解算法
该算法首先需要引入两个辅助因子y, u,将原潮流方程h(x) = p转化为一组欠定方程、一组超定方程与一组辅助向量间的关系函数。进行该步骤的目的是为后续的两步法求解提供合适的方程形式。
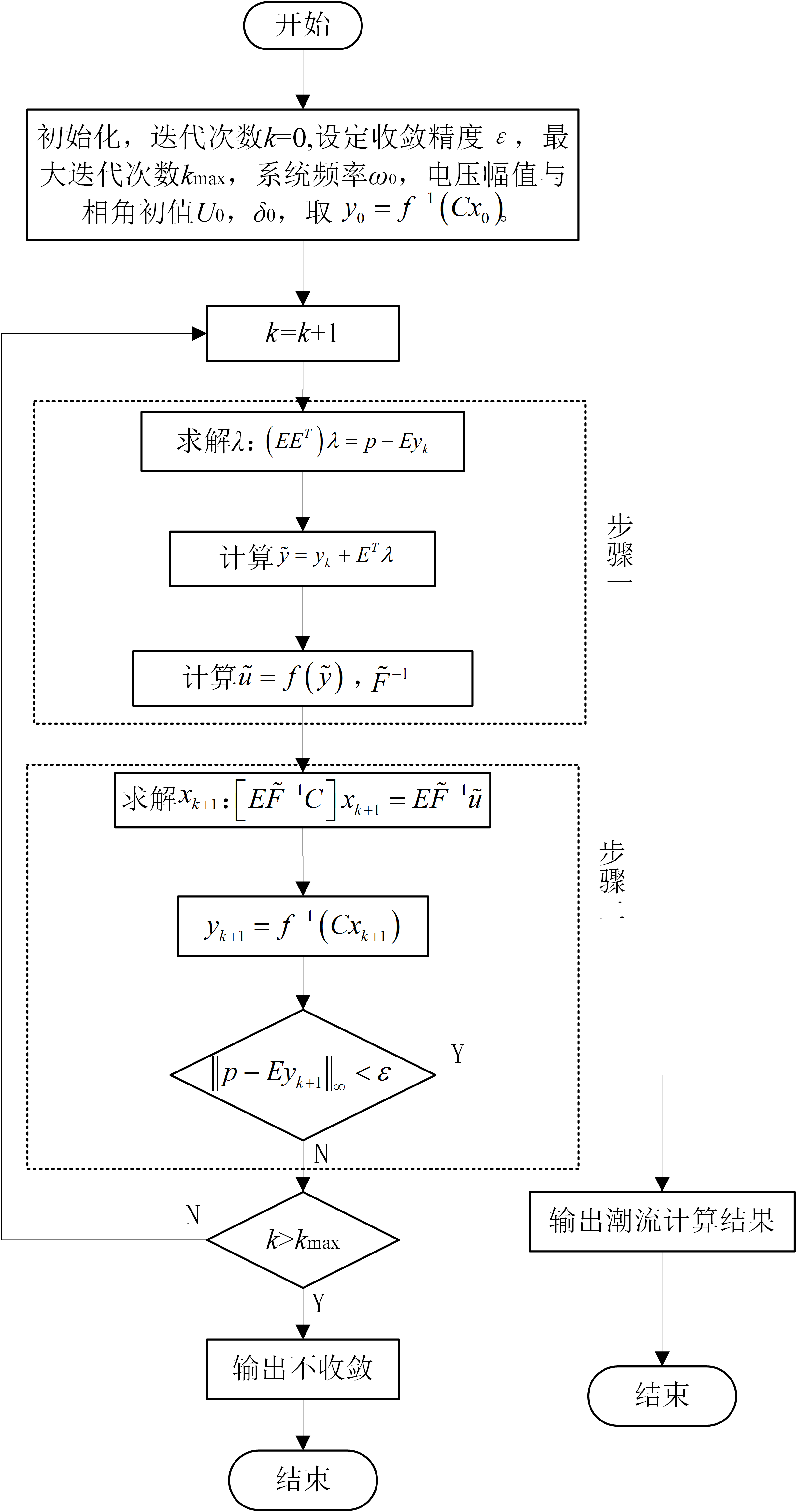
两步法求解的具体过程如下图所示。两步法求解的核心思想是希望找到一个比当前迭代点更接近真实解的线性化点,以此来提高算法的鲁棒性。因此,步骤一通过求解方程获得λ,借助λ可以获得一个比当前迭代值更接近真实解的线性化点,以提高算法对初值的鲁棒性。步骤二根据上一步获得的新线性化点,直接解出下一迭代步变量值xk+1,可以起到减少计算量的作用。
<h1 id=) 结果分析
结果分析本文对算法的结果正确性,鲁棒性以及计算效率进行了分析。在结果正确性方面,通过与牛拉法的对比,两种算法的潮流计算结果完全一致,验证了本文算法的正确性。
在鲁棒性方面,本文通过随机产生的变量初值进行100次计算,记录不同算法的不收敛次数,进行鲁棒性对比。结果显示,本文算法在初值波动范围增大时依然可以保持良好的鲁棒性。
在计算效率方面,本文使用不同算法进行了1000次蒙特卡洛模拟。结果显示,本文算法为提高鲁棒性,相比牛拉法一定程度上牺牲了计算效率,但也仅差6.91%。而相较基于LM算法的潮流计算方法,在计算效率方面有着明显提高。
后续研究方向
如何利用该方法进行其他微电网相关的分析计算,例如连续潮流计算、鞍结分岔点快速求取等,将是作者下一步重点关注方向。
文章链接
林立亨,董树锋,朱承治,唐坤杰,宋永华.基于辅助因子两步求解算法的孤岛微电网潮流计算[J].电网技术
若对于本文有任何疑问或者建议,请联系作者21810116@zju.edu.cn。
版权声明:本文由SGOOL团队创作和发表,转载或引用本文内容请注明作者及出处。