智能配电网络建模与分析
配电网潮流计算
2020年
本次课的内容
利用配电网络的元建模型,推导出配电网络潮流和短路的分析方法:
(1)梯形迭代法
(2)基于回路电流法的配电网三相潮流算法
(3)短路分析
配电网潮流计算
是配电网设计、调度运行、无功优化以及其他相关方面研究工作的基础。
需要已知的量:
需要已知变电站的三相电压以及所有负荷的负荷模型(恒定复功率,恒定阻抗,恒定电流或组合模型)。有时,变电站提供给馈线的输入复功率也是已知的。
获得的信息:
各节点处的电压大小与相角、线路潮流、各线路的功率损耗、总的输入有功功率和无功功率、线路总有功功率损耗、根据负荷的指定模型确定负荷的功率。
配电网潮流计算的梯形迭代法
由于配电馈线是辐射状的,即各条线路有明确的始端与末端。为了提高收敛性,辐射状网络的潮流计算通常不使用输电网潮流计算中常用的牛顿迭代法,而是使用专门为辐射状网络设计的迭代方法。
线性网络
对线性系统梯形网络理论的修改可得出用于配电网潮流计算的鲁棒迭代方法。由于假定大多数负荷是恒功率的,因此配电网络是非线性的,可以通过修改线性系统所采用的方法从而考虑配电馈线的非线性特性。

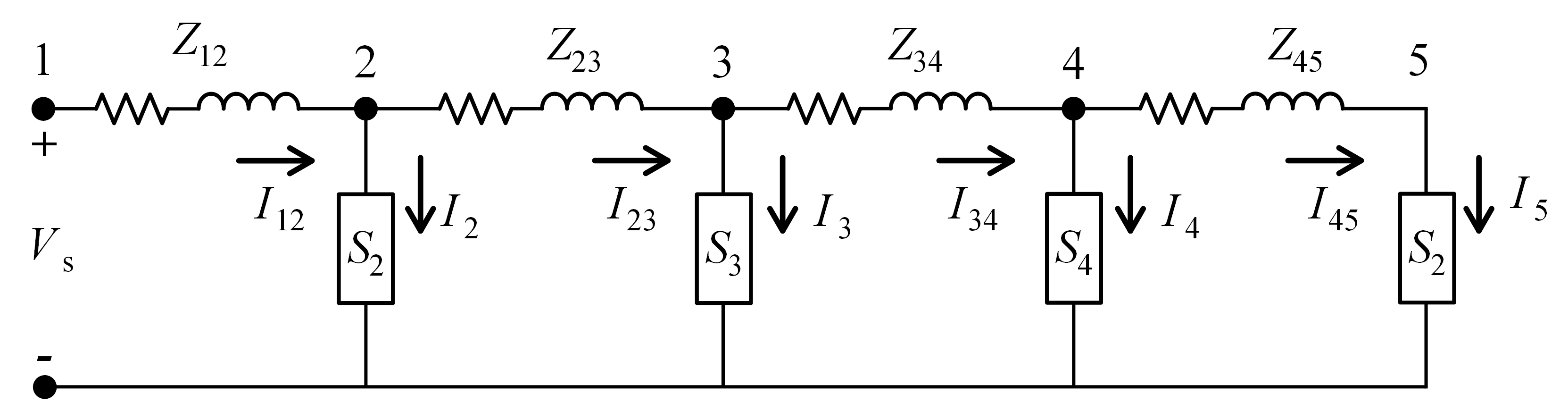
计算该网络潮流的方案
假设末端负荷的电压为\(V_{5}\),然后计算负荷电流\(I_{5}\)为:
\[\begin{eqnarray} \label{c1} I_{5}=\frac{V_{5}}{ZL_{5}} \end{eqnarray}\]线电流\(I_{45}\)等于负荷电流\(I_{5}\)。得到节点4处的电压(\(V_{4}\)):
\[\begin{eqnarray} \label{c2} V_{4}=V_{5}+Z_{45}\cdot I_{45} \end{eqnarray}\]容易计算负荷电流\(I_{4}\),求得线电流\(I_{34}\):
\[\begin{eqnarray} \label{c3} I_{34}=I_{45}+I_{4} \end{eqnarray}\]节点电压\(V_{3}\)可以由基尔霍夫电压定律确定。重复该过程直到在源处计算出电压(\(V_{1}\))。
将计算出的电压\(V_{1}\)与给定实际电压\(V_{\text{s}}\)进行比较,二者之间存在差异。实际电压与计算所得电压的比率可确定为:
\[\begin{eqnarray} \label{c4} r=\frac{V_{\text{s}}}{V_{1}} \end{eqnarray}\]由于网络是线性的,因此网络中的所有线路和负荷的电流以及节点电压都可以乘以上述比率,得到最终结果。
非线性网络
用恒定复功率负荷替换所有恒定阻抗负荷,则上图的线性梯形网络被修改为非线性梯形网络:

针对线性网络的计算过程同样可应用于非线性网络,唯一的区别是每个节点的负荷电流由下式计算:
\[\begin{eqnarray} \label{c5} I_{n}=\left ( \frac{S_{n}}{V_{n}} \right )^{*} \end{eqnarray}\]计算非线性网络潮流的方案
由于网络是非线性的,因此将电流和电压乘以给定电压与计算所得电压的比率无法得到正确结果。对梯形网络理论的修正是再进行前推计算。 可以通过下式计算节点2处的电压:
\[\begin{eqnarray} \label{c6} V_{2}=V_{\text{s}}-Z_{12}\cdot I_{12} \end{eqnarray}\]对每条线路重复上述计算,直到在节点5处得到一个新的电压值。使用节点5处的新电压,开始第二次回代计算,这样又可得到一个新的电源电压计算结果。
不断重复前推和回代计算过程,直到电源节点的计算电压和给定电压之间的差值在容许的误差范围内。
例题一
【例 6.1】 一单相系统如下图所示。 线路阻抗是\[z=0.1864+\text{j}0.3728 \ \Omega /\text{km}\]
线路1-2的阻抗为:
\[Z_{12}=\left ( 0.1864+\text{j}0.3728 \right )\cdot \frac{914.4}{1000}=0.1705+\text{j}0.3409 \ \text{(}\Omega \text{)}\]
线路2-3的阻抗为:
\[Z_{23}=\left ( 0.1864+\text{j}0.3728 \right )\cdot \frac{1219.2}{1000}=0.2273+\text{j}0.4545 \ \text{(}\Omega \text{)}\]
负荷为:
\[\begin{gather*} S_{2}=1500+\text{j}750 \ \text{kVA}\\ S_{3}=900+\text{j}500 \ \text{kVA} \end{gather*}\]节点1处源电压为7200 V。求经过一次完整前推回代计算后的节点电压。
【解答】 回代过程开始时,假设节点3处的电压为7200 V,相角为0。节点3处负荷电流为
\[I_{3}=\left ( \frac{\left ( 900+\text{j}500 \right )\cdot 1000}{7200\angle{0}} \right )^{*}=143.0\angle{-29.0} \ \text{(A)}\]
线路2-3处电流为
\[I_{23}=I_{3}=143.0\angle{-29.0} \ \text{(A)}\]
节点2处电压为
\[V_{2}=V_{3}+Z_{23}\cdot I_{23}=7200\angle{0}+\left ( 0.2273+\text{j}0.4545 \right )\cdot 143.0\angle{-29.0}=7260.1\angle{0.32} \ \text{(V)}\]
节点2处负荷电流为
\[I_{2}=\left ( \frac{\left ( 1500+\text{j}750 \right )\cdot 1000}{7260 \cdot 1\angle{0.32}} \right )^{*}=231.0\angle{-26.3} \ \text{(A)}\]
线路1-2处电流为
\[I_{12}=I_{23}+I_{2}=373.9\angle{-27.3} \ \text{(A)}\]
节点1处电源电压为
\[V_{1}=V_{2}+Z_{12}\cdot I_{12}=7376.2\angle{0.97} \ \text{(V)}\]
此时将节点1处计算得到的电压与给定的电源电压大小进行比较:
\[Error=\left | \left | V_{\text{s}} \right |-\left | V_{1} \right | \right |=176.2 \ \text{(V)}\]
如果误差小于规定值,则已得到最终结果。 如果误差大于规定值,则开始前推计算。通常误差允许值为0.001pu,在7200 V基准电压下为7.2 V.由于此情况下的误差大于允许误差,因此通过将节点1处的电压设置为给定的电源电压来开始前推计算:
\[V_{1}=V_{\text{s}}=7200\angle{0} \ \text{(V)}\]
计算节点2的电压时使用节点1电压值和回代计算得到的线电流:
\[V_{2}=V_{1}-Z_{12}\cdot I_{12}=7200\angle{0}-\left ( 0.1705+\text{j}0.3409 \right )\cdot 373.9\angle{-27.2}=7085.4\angle{-0.68} \ \text{(V)}\]
继续向网络末端计算,在回代计算中得到的所有电流都用于前推计算。
\[V_{3}=V_{2}-Z_{23}\cdot I_{23}=7026.0\angle{-1.02} \ \text{(V)}\]
这样就完成了第一次迭代。此后将重复回代计算,但节点3使用的是计算得到的新电压,而不是最初假设的电压。
梯形迭代法步骤
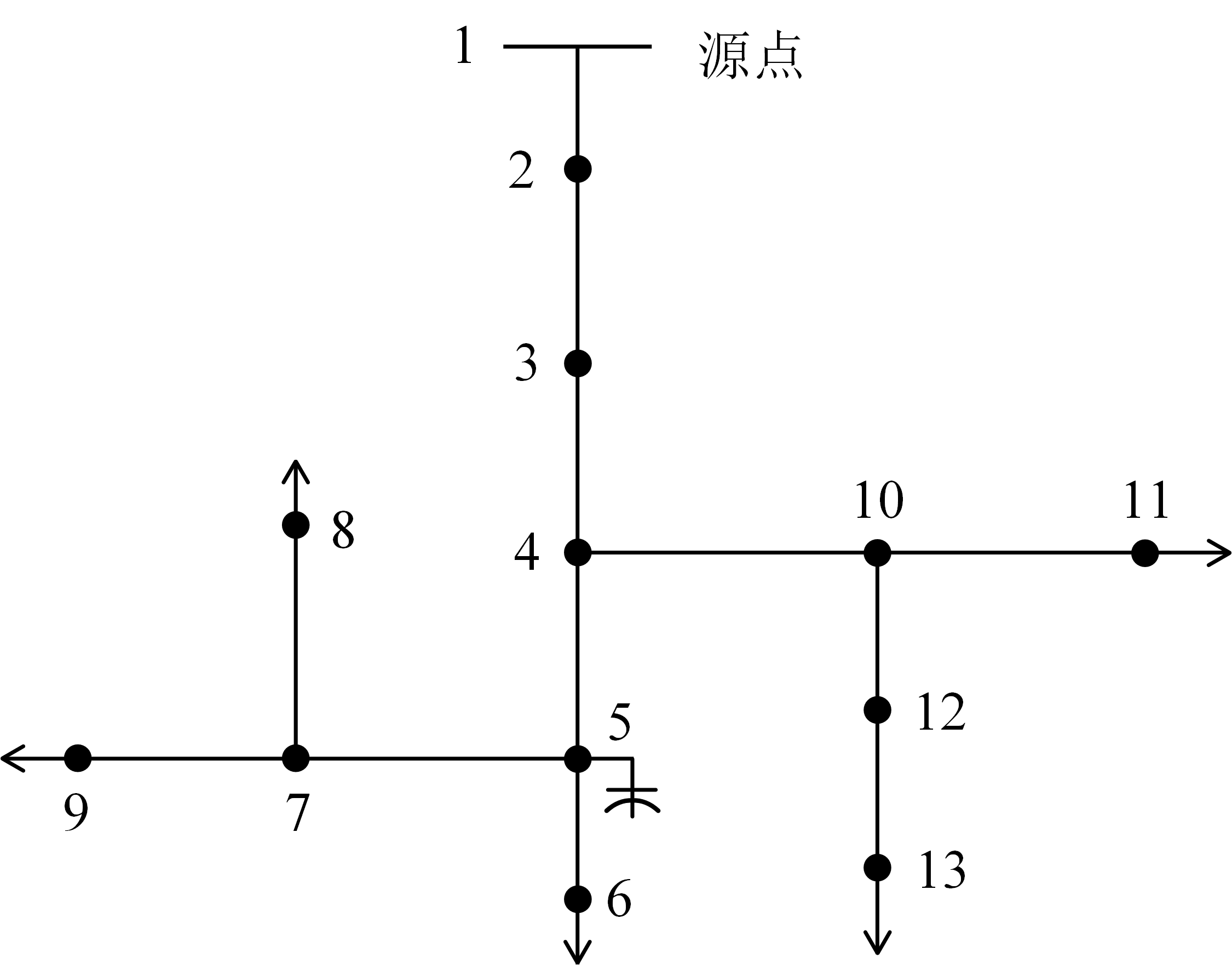
(1)假设末端节点(6,8,9,11,13)的三相电压初始值,通常取额定电压。
(2)从节点13开始,计算节点电流(负荷电流加电容器电流)。
(3)利用该电流,应用基尔霍夫电压定律计算12和10处的节点电压。
(4)节点10被称为“结”节点,因为横向从节点沿两个方向分支。对于此馈线,转至节点11并计算节点电流。 使用该电流计算节点10处的电压,将此称为“节点10处的最新电压”。
(5)使用节点10处的最新电压值,计算节点10处的节点电流(如果存在)。
(6)应用基尔霍夫电流定律来确定从节点4到节点10的电流。
(7)计算节点4处电压。
(8)节点4是结节点。 选择节点4的其他下游末端节点开始向节点4进行回代计算。
(9)选择节点6,计算节点电流,然后计算连接节点5处的电压。
(10)转到下游末端节点8,计算节点电流,然后计算接线节点7处的电压。
(11)转到下游末端节点9,计算节点电流,然后计算接线节点7处的电压。
(12)使用节点7电压的最新值计算节点7处的节点电流。
(13)在节点7处应用KCL以计算从节点5到节点7的线段上的当前电流。
(14)计算节点5处的电压。
(15)在节点5处计算节点电流。
(16)在节点5处应用KCL到确定从节点4到节点5的当前电流。
(17)计算节点4处的电压。
(18)在节点4处计算节点电流。
(19)在节点4处应用KCL以计算从节点3到节点4的当前电流。
(20)计算节点3的电压。
(21)计算节点3的节点电流。
(22)在节点3处应用KCL以计算节点2到节点3的当前流量。
(23)计算节点2的电压。
(24)计算节点2的节点电流。
(25)在节点2处应用KCL。
(26)计算节点1的电压。
(27)将节点1的计算电压与指定的电源电压进行比较。
(28)如果不在容许误差范围内,则使用给定的电源电压和从节点1到节点2的回代计算电流,计算节点2处的新电压。
(29)使用新的上游电压和线路电流继续前推计算新的下游电压。
(30)当所有端节点上的新电压计算完成时,完成前推计算。
(31)这完成了第一次迭代。
(32)重复回代计算,现在只使用新的末端电压而不是第一次迭代中的假设电压。
(33)继续回代和前推计算,直到电源处的计算电压在允许误差范围内。
(34)此时,所有节点电压和所有线路上的电流都是已知的,得到最终计算结果。
不对称三相馈线
简要介绍梯形迭代算法如何用于不对称三相馈线。
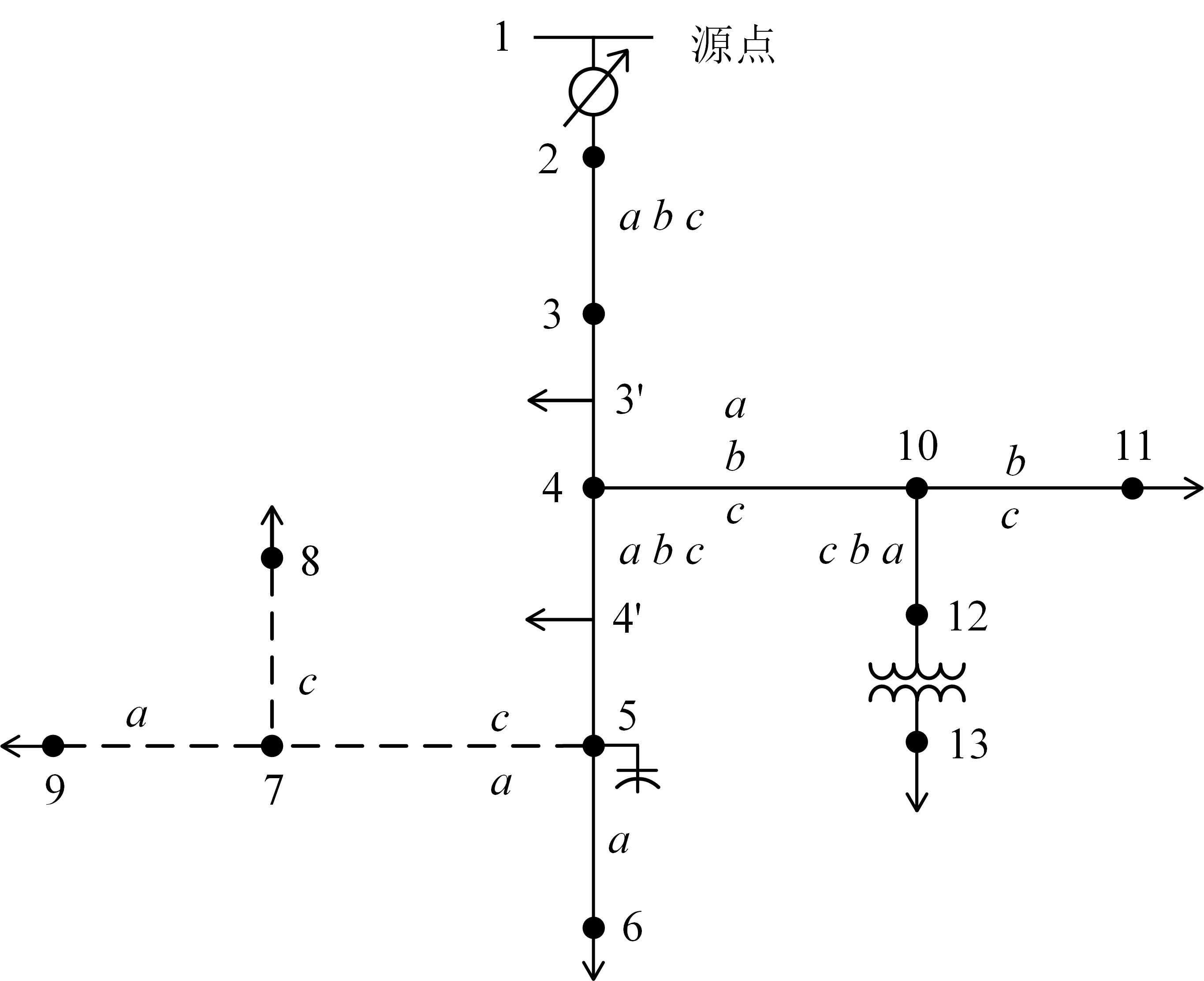
上图的馈线可以分为“串联”元件和“分流”元件。
实线表示架空线,虚线表示地下线。图中显示了所有线段的相位。 在第2章中,介绍了用于计算架空线和地下线路线路阻抗的Carson方程的应用。 在该章指出了两相和单相线可由\(3\times 3\)矩阵表示,其中在缺失相的行和列中设置零。还介绍了计算架空线路和地下线路并联电容电纳的方法。大多数情况下,线路的并联电容可以忽略不计,但对于较长的地下线路,应考虑并联电容。
串联元件
配电馈线的串联元件包括:配电线路、变压器和电压调节器。在前面的章节中已经建立了每个串联元件的模型。在各种情况下,模型(三相、两相和单相)都是广义矩阵。如图是串联元件的通用模型:

输入(节点\(n\))和输出(节点\(m\))电压、电流的通用方程式:
\[\begin{gather} \left [ V_{abc} \right ]_{n}=\left [ a \right ]\cdot \left [ V_{abc} \right ]_{m}+\left [ b \right ]\cdot \left [ I_{abc} \right ]_{m} \label{c7}\\ \left [ I_{abc} \right ]_{n}=\left [ c \right ]\cdot \left [ V_{abc} \right ]_{m}+\left [ d \right ]\cdot \left [ I_{abc} \right ]_{m} \label{c8} \end{gather}\]关于输出(节点\(m\))和输入(节点\(n\))电压的通用等式:
\[\begin{equation} \label{c9} \left [ V_{abc} \right ]_{m}=\left [ A \right ]\cdot \left [ V_{abc} \right ]_{n}-\left [ B \right ]\cdot \left [ I_{abc} \right ]_{m} \end{equation}\]上式中,对于四线三角形馈线,电压是线对中性线的,对于三线三角形系统,电压是等效的线对中性线的。 对于电压调节器,连接到四线星形的端子和连接到三线三角形的电压是线对中性线的。
分流器件
配电馈线的分流元件包括:点负荷、分布式负荷和电容器组。
- 点负荷
位于节点处,可以是三相、两相或单相的,并以星形或三角形方式连接。
可以建模为恒定功率、恒定电流、恒定阻抗或三者的组合。
- 分布式负荷
可以是三相、两相或单相的,并以星形或三角形方式连接。
可以建模为恒定功率、恒定电流、恒定阻抗或三者的组合。
当线段上的负荷沿着线段的长度均匀分布时,分布式负荷等效于三分之二的负荷量连接在位于线路四分之一点的虚拟节点处,剩余的三分之一负荷连接在线路段的末端。
- 电容器组
位于节点处,可以是三相、两相或单相的,并且可以以星形或三角形方式连接。
建模为恒定导纳形式。
例题二
【例 6.2】 一个简单的配电网络如下图所示,对于图中的系统,无穷大母线的线电压三相对称,为12.47 kV。从节点1到节点2的线路是三线三角形,长度为609.6 m,线路构造如课本上图2-7所示。从节点3到节点4的四线星形负荷线路的构造如图2-7所示,长度为762.0m。
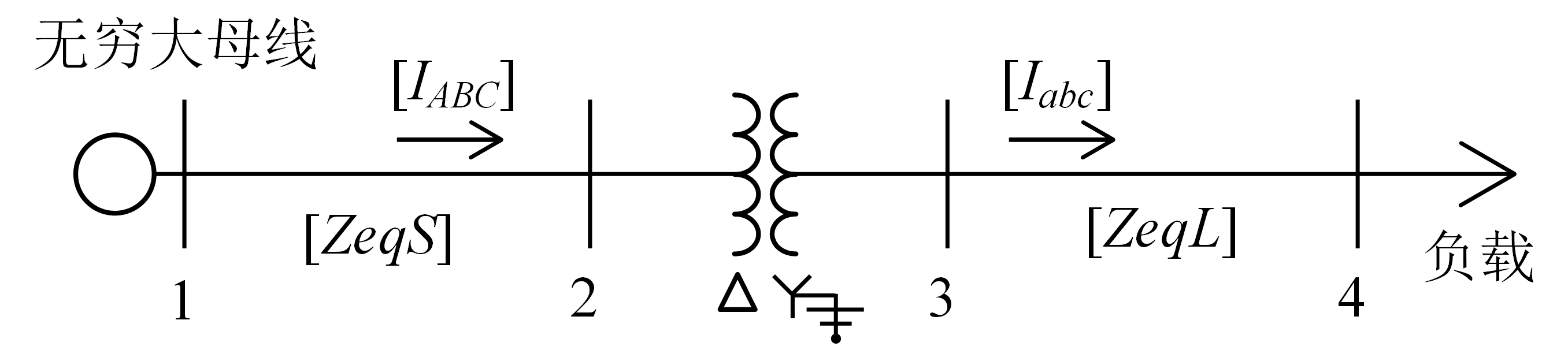
两条线路的相导线均使用336,400 26/7钢芯铝绞线,四线星形线上的中性线为4/0 6/1钢芯铝绞线。由于线路较短,线路导纳可忽略。两条线路的相阻抗矩阵为
变压器组为三角形 - 接地星形接法,由三个单相变压器组成,每个变压器额定值为
\[2000\ \text{kVA},\ 12.47\text{ kV-}2.4\ \text{kV},\ Z=1.0+\text{j}6.0\%\]
不对称的三相星形连接负荷为
\[\begin{gather*} S_{a}=750\ \text{kVA} \ \ \ \text{滞后功率因数}0.85\\ S_{b}=1000\ \text{kVA} \ \ \ \text{滞后功率因数}0.90\\ S_{c}=1250\ \text{kVA} \ \ \ \text{滞后功率因数}0.95 \end{gather*}\]计算该配电网络的潮流。
解答
在开始迭代之前,必须计算三个串联元件的广义矩阵。
电源线路段:
由式(2.124)和式(2.133):
\[\left [ a_{1} \right ]=\left [ d_{1} \right ]=\left [ U \right ]=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0\\ 0& 0 & 1 \end{bmatrix}\]
由式(2.125):
\[\left [ b_{1} \right ]=\left [ ZeqS_{ABC} \right ]=\begin{bmatrix} 0.1414+\text{j}0.5353 & 0.0361+\text{j}0.3225 &0.0361+\text{j}0.2752 \\ 0.0361+\text{j}0.3225 & 0.1414+\text{j}0.5353 & 0.0361+\text{j}0.2955\\ 0.0361+\text{j}0.2752 & 0.0361+\text{j}0.2955 & 0.1414+\text{j}0.5353 \end{bmatrix}\]
由式(2.132):
\[\left [ c_{1} \right ]=\left [ 0 \right ]\]
由式(2.142):
\[\left [ A_{1} \right ]=\left [ a_{1} \right ]^{-1}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\]
由式(2.143):
\[\left [ B_{1} \right ]=\left [ a_{1} \right ]^{-1}\cdot \left [ b_{1} \right ]=\begin{bmatrix} 0.1414+\text{j}0.5353 & 0.0361+\text{j}0.3225 &0.0361+\text{j}0.2752 \\ 0.0361+\text{j}0.3225 & 0.1414+\text{j}0.5353 & 0.0361+\text{j}0.2995\\ 0.0361+\text{j}0.2752 & 0.0361+\text{j}0.2955 & 0.1414+\text{j}0.5353 \end{bmatrix}\]
负荷线路段(使用与电源线路段相同的公式):
\[\begin{gather*} \left [ a_{2}\right ]=\left [ d_{2} \right ]=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\\ \left [ b_{2} \right ]=\begin{bmatrix} 0.1907+\text{j}0.5035 & 0.0607+\text{j}0.2302 &0.0598+\text{j}0.1751 \\ 0.0607+\text{j}0.2302 & 0.1939+\text{j}0.4885 & 0.0614+\text{j}0.1931\\ 0.0598+\text{j}0.1751& 0.0614+\text{j}0.1931 & 0.1921+\text{j}0.4970 \end{bmatrix}\\ \left [ c_{2} \right ]=\left [ 0 \right ]\\ \left [ A_{2} \right ]=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 &0 \\ 0 & 0 & 1 \end{bmatrix}\\ \left [ B_{2} \right ]=\begin{bmatrix} 0.1907+\text{j}0.5035 & 0.0607+\text{j}0.2302 &0.0598+\text{j}0.1751 \\ 0.0607+\text{j}0.2302 & 0.1939+\text{j}0.4885 & 0.0614+\text{j}0.1931\\ 0.0598+\text{j}0.1751& 0.0614+\text{j}0.1931 & 0.1921+\text{j}0.4970 \end{bmatrix} \end{gather*}\]变压器:
将变压器阻抗转换为以低压绕组为参考的实际值,单位为\(\Omega\)。
\[\begin{gather*} Z_{\text{base}}=\frac{2.4^{2}\cdot 1000}{2000}=2.88 \ \text{(}\Omega \text{)}\\ Zt_{\text{kw}}=\left ( 0.01+\text{j}0.06 \right )\cdot 2.88=0.0288+\text{j}0.1728 \ \text{(}\Omega \text{)} \end{gather*}\]变压器的相阻抗矩阵为
\[\left [ Zt_{abc} \right ]=\begin{bmatrix} 0.0288+\text{j}0.1728 & 0 & 0\\ 0 & 0.0288+\text{j}0.1728 & 0\\ 0& 0 & 0.0288+\text{j}0.1728 \end{bmatrix} \ \text{(}\Omega \text{)}\]
匝数比和变压比分别为
\[n_{\text{t}}=\frac{12.47}{2.4}=5.1958, \ \ \ a_{\text{t}}=\frac{12.47}{\sqrt{3}\cdot 2.4}=2.9998\]
计算变压器的广义矩阵。由式(4.22)可得
\[\left [ a_{\text{t}} \right ]=\frac{-n_{\text{t}}}{3}\cdot \begin{bmatrix} 0 & 2 &1 \\ 1 & 0 &2 \\ 2 & 1 & 0 \end{bmatrix}= \begin{bmatrix} 0 & -3.4639 & -1.7319\\ -1.7319 & 0 &-3.4639 \\ -3.4639 & -1.7319 & 0 \end{bmatrix}\]
由式(4.26)可得
\[\begin{gather*} \left [ b_{\text{t}} \right ]=\frac{-n_{\text{t}}}{3}\cdot \begin{bmatrix} 0 & 2\cdot Z_{\text{t}} &Z_{\text{t}} \\ Z_{\text{t}} & 0 & 2\cdot Z_{\text{t}}\\ 2\cdot Z_{\text{t}} & Z_{\text{t}} & 0 \end{bmatrix}\\ \left [ b_{\text{t}} \right ]=\begin{bmatrix} 0 & -0.0998-\text{j}0.5986 &-0.0499-\text{j}0.2993 \\ -0.0499-\text{j}0.2993 & 0 & -0.0998-\text{j}0.5986\\ -0.0998-\text{j}0.5986 & -0.0499-\text{j}0.2993 & 0 \end{bmatrix} \end{gather*}\]由式(4.41)可得
\[\left [ c_{\text{t}} \right ]=\begin{bmatrix} 0 &0 & 0\\ 0& 0& 0\\ 0& 0 & 0 \end{bmatrix}\]
由式(4.40)可得
\[\left [ d_{\text{t}} \right ]=\frac{1}{n_{\text{t}}}\cdot \begin{bmatrix} 1 & -1 & 0\\ 0& 1 &-1 \\ -1 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 0.1925 & -0.1925 & 0\\ 0& 0.1925 & -0.1925\\ -0.1925 & 0 & 0.1925 \end{bmatrix}\]
由式(4.32)可得
\[\left [ A_{\text{t}} \right ]=\frac{1}{n_{\text{t}}}\cdot \begin{bmatrix} 1 & 0 & -1\\ -1 & 1 &0 \\ 0& -1 & 1 \end{bmatrix}=\begin{bmatrix} 0.1925 & 0 & -0.1925\\ -0.1925 & 0.1925 &0 \\ 0 & -0.1925 & 0.1925 \end{bmatrix}\]
由式(4.34)可得
\[\left [ B_{\text{t}} \right ]=\left [ Zt_{abc} \right ]=\begin{bmatrix} 0.0288+\text{j}0.1728 & 0 &0 \\ 0& 0.0288+\text{j}0.1728 &0 \\ 0& 0 & 0.0288+\text{j}0.1728 \end{bmatrix}\]
确定无穷大母线的线电压和线到中性点电压:
\[\begin{gather*} \left [ ELL_{\text{s}} \right ]=\begin{bmatrix} 12470\angle{30}\\ 12470\angle{-90}\\ 12470\angle{150} \end{bmatrix} \ \text{(V)}\\ \left [ ELN_{\text{s}} \right ]=\begin{bmatrix} 7199.6\angle{0}\\ 7199.6\angle{-120}\\ 7199.6\angle{120} \end{bmatrix} \ \text{(V)} \end{gather*}\]将节点4处的线电压设置为滞后30\(^{\circ}\)的额定电压:
\[\left [ V_{4} \right ]=\begin{bmatrix} 2400\angle{-30}\\ 2400\angle{-150}\\ 2400\angle{90} \end{bmatrix} \ \text{(V)}\]
确定节点4的负荷:
\[\left [ S_{4} \right ]=\begin{bmatrix} 750\angle{31.79}\\ 1000\angle{25.84}\\ 1250\angle{18.19} \end{bmatrix} \ \text{(kVA)}\]
通过计算节点4处的负荷电流开始回代计算:
\[\left [ I_{4i} \right ]=\left ( \frac{S_{i}\cdot 1000}{V_{4i}} \right )^{*}=\begin{bmatrix} 312.5\angle{-61.8}\\ 416.7\angle{-175.8}\\ 520.8\angle{71.8} \end{bmatrix} \ \text{(A)}\]
计算节点3的电压和电流:
\[\begin{gather*} \left [ V_3 \right ]=\left [ a_{2} \right ]\cdot \left [ V_{4} \right ]+\left [ b_{2} \right ]\cdot \left [ I_4 \right ]=\begin{bmatrix} 2470.9\angle{-29.5}\\ 2534.4\angle{-148.4}\\ 2509.5\angle{94.1} \end{bmatrix} \ \text{(V)}\\ \left [ I_3 \right ]=\left [ c_{2} \right ]\cdot \left [ V_{4} \right ]+\left [ d_{2} \right ]\cdot \left [ I_4 \right ]=\begin{bmatrix} 312.5\angle{61.8}\\ 416.7\angle{-175.8}\\ 520.8\angle{71.8} \end{bmatrix} \ \text{(A)} \end{gather*}\]计算节点2的电压和电流:
\[\begin{gather*} \left [ V_2 \right ]=\left [ a_{\text{t}} \right ]\cdot \left [ V_{3} \right ]+\left [ b_{\text{t}} \right ]\cdot \left [ I_3 \right ]=\begin{bmatrix} 7956.4\angle{3.3}\\ 7344.5\angle{-113.4}\\ 7643.0\angle{120.5} \end{bmatrix} \ \text{(V)}\\ \left [ I_2 \right ]=\left [ c_{\text{t}} \right ]\cdot \left [ V_{3} \right ]+\left [ d_{\text{t}} \right ]\cdot \left [ I_3 \right ]=\begin{bmatrix} 118.2\angle{-23.5}\\ 150.3\angle{-137.8}\\ 148.3\angle{88.9} \end{bmatrix} \ \text{(A)} \end{gather*}\]计算节点1处的等效线到中性点电压和线电流:
\[\begin{gather*} \left [ V_1 \right ]=\left [ a_{1} \right ]\cdot \left [ V_{2} \right ]+\left [ b_{1} \right ]\cdot \left [ I_2 \right ]=\begin{bmatrix} 7985.9\angle{3.4}\\ 7370.6\angle{-113.2}\\ 7673.6\angle{120.7} \end{bmatrix} \ \text{(V)}\\ \left [ I_1 \right ]=\left [ c_{1} \right ]\cdot \left [ V_{2} \right ]+\left [ d_{1} \right ]\cdot \left [ I_2 \right ]=\begin{bmatrix} 118.2\angle{-23.5}\\ 150.3\angle{-137.8}\\ 148.3\angle{88.9} \end{bmatrix} \ \text{(A)} \end{gather*}\]节点1处的线电压为
\[\left [ VLL_1 \right ]=\left [ D \right ]\cdot \left [ V_1 \right ]=\begin{bmatrix} 13067.5\angle{33.7}\\ 13411.4\angle{-85.7}\\ 13375.9\angle{152.7} \end{bmatrix} \ \text{(V)}\]
计算线电压误差的大小:
\[\left [ Error \right ]_{\text{pu}}=\frac{\left | \left [ ELL_{\text{s}}-VLL_1 \right ] \right |}{12470}=\begin{bmatrix} 0.0809\\ 0.1086\\ 0.0876 \end{bmatrix}\]
由于这些误差大于0.001pu的典型允许误差,因此开始前推计算。前推计算使用电源处的等效线到中性点电压作为节点1电压,电流为回代计算的线电流。
\[\begin{gather*} \left [ V_2 \right ]=\left [ A_{\text{1}} \right ]\cdot \left [ VLN_{\text{s}} \right ]-\left [ B_{1} \right ]\cdot \left [ I_{2} \right ]=\begin{bmatrix} 7171.1\angle{-0.1}\\ 7176.7\angle{-120.2}\\ 7169.3\angle{119.8} \end{bmatrix} \ \text{(V)}\\ \left [ V_3 \right ]=\left [ A_{\text{t}} \right ]\cdot \left [ V_{2} \right ]-\left [ B_{\text{t}} \right ]\cdot \left [ I_{3} \right ]=\begin{bmatrix} 2354.0\angle{-31.2}\\ 2351.0\angle{-151.6}\\ 2349.9\angle{87.8} \end{bmatrix} \ \text{(V)}\\ \left [ V_4 \right ]=\left [ A_{2} \right ]\cdot \left [ V_{3} \right ]-\left [ B_{2} \right ]\cdot \left [ I_{4} \right ]=\begin{bmatrix} 2283.7\angle{-31.7}\\ 2221.4\angle{-153.6}\\ 2261.0\angle{83.2} \end{bmatrix} \ \text{(V)} \end{gather*}\]这样就完成了第一次迭代。第二次迭代使用节点4电压的新值计算节点4的负荷电流。回代计算使用这些新电流。反复进行回代和前推计算,直到电源处的误差小于每单位0.001。经过4次迭代后,计算结果已收敛到每单位0.0003的误差。得到节点4处的负荷电压为
\[\left [ V_{\text{4final}} \right ]=\begin{bmatrix} 2278.7\angle{-31.8}\\ 2199.8\angle{-153.5}\\ 2211.2\angle{83.1} \end{bmatrix} \ \text{(V)}\]
在120 V基准下,最终电压为
\[\left [ V_{4\ 120} \right ]=\begin{bmatrix} 113.9\angle{-31.8}\\ 110.0\angle{-153.5}\\ 110.6\angle{83.1} \end{bmatrix} \ \text{(V)}\]
节点4处的电压低于所需的120(121±1)V。这些低电压可以通过在变压器的低压端(节点3)上安装星形连接的三个步进电压调节器来校正。新的网络结构如图所示。对于调节器,电压互感器比率为2400V-120V(\(N_{\text{pt}}=20\)),并选择合适的\(CT\)比率来承载变压器组的额定电流。额定电流为
\[I_{\text{rated}}=\frac{6000}{\sqrt{3}\cdot 2.4}=832.7\]

\(CT\)比率选为1000A-5A = \(CT\) = 200。 使用两个节点处的计算收敛电压计算节点3和节点4之间的等效相阻抗。 这样做可以确定补偿器的\(R\)和\(X\)设置:
\[Zeq_{i}=\frac{V_{3i}-V_{4i}}{I_{3i}}=\begin{bmatrix} 0.1414+\text{j}0.1829\\ 0.2078+\text{j}0.2826\\ 0.0889+\text{j}0.3833 \end{bmatrix} \ \text{(}\Omega \text{)}\]
三个调节器应具有相同的\(R\)和\(X\)补偿器设置。阻抗的平均值为
\[Z_{\text{avg}}=\frac{1}{3}\cdot \sum_{k=1}^{3}Zeq_{k}=0.1461+\text{j}0.2830 \ \text{(}\Omega \text{)}\]
以V为单位的补偿器阻抗值由式(3.82)给出:
\[R'+\text{j}X'=\left ( 0.1461+\text{j}0.2830 \right )\cdot \frac{1000}{20}=7.3+\text{j}14.2 \ \text{(V)}\]
以\(\Omega\)为单位的补偿器设置值为
\[R_{\Omega }+\text{j}X_{\Omega }=\frac{7.3+\text{j}14.2}{5}=1.46+\text{j}2.84 \ \text{(}\Omega \text{)}\]
当调节器处于中性位置时,在给定条件下输入补偿器电路的电压是
\[Vreg_{i}=\frac{V_{3i}}{PT}=\begin{bmatrix} 117.5\angle{-31.2}\\ 117.1\angle{-151.7}\\ 116.7\angle{87.8} \end{bmatrix} \ \text{(V)}\]
利用输入电压和补偿器电流,计算补偿器电路中的电压继电器两端的电压:
\[\left [ V_{\text{relay}} \right ]=\left [ V_{\text{reg}} \right ]-\left [ Z_{\text{comp}} \right ]\cdot \left [ I_{\text{comp}} \right ]=\begin{bmatrix} 113.0\angle{-32.5}\\ 111.2\angle{-153.8}\\ 110.0\angle{84.7} \end{bmatrix} \ \text{(V)}\]
注意其与节点4上120 V基准的实际电压相比的差距。假设电压电平设置为121 V,带宽为2 V。调节器将改变抽头直到相电压至少为120 V。通过继电器上的计算电压,每个调节器将移动的大致距离可通过以下公式计算:
\[Tap_{i}=\frac{120-\left | V_{4i} \right |}{0.75}=\begin{bmatrix} 9.3\\ 11.7\\ 13.4 \end{bmatrix}\approx \begin{bmatrix} 9\\ 12\\ 13 \end{bmatrix}\]
当抽头设置为9、12和13时,调节器的\([a]\)矩阵为
\[\begin{gather*} \left [ a_{\text{r}} \right ]=\begin{bmatrix} 1.0-0.00625\cdot Tap_{1} & 0 &0 \\ 0& 1.0-0.00625\cdot Tap_{2} &0 \\ 0& 0 & 1.0-0.00625\cdot Tap_{3} \end{bmatrix}\\ \left [ a_{\text{r}} \right ]=\begin{bmatrix} 0.9438 & 0 &0 \\ 0& 0.9250 &0 \\ 0& 0 &0.9188 \end{bmatrix} \end{gather*}\]调节器的\([d]\)矩阵为
\[\left [ d_{\text{r}} \right ]=\left [ a_{\text{r}} \right ]^{-1}=\begin{bmatrix} 1.0596 & 0 &0 \\ 0& 1.0811 &0 \\ 0& 0 &1.0884 \end{bmatrix}\]
\([b]\)、\([c]\)和\([B]\)矩阵为零,\([A]\)矩阵由下式给出:
\[\left [ A_{\text{r}} \right ]=\left [ a_{\text{r}} \right ]^{-1}=\begin{bmatrix} 1.0596 & 0 &0 \\ 0& 1.0811 &0 \\ 0& 0 &1.0884 \end{bmatrix}\]
后续步骤是执行与前述相同的梯形迭代,调节器是节点3r和3之间的附加元件,如图所示。系统在4次迭代后收敛,节点4的以120 V为基准的电压为
\[\left [ V_{4\ 120} \right ]=\begin{bmatrix} 121.0\angle{-31.8}\\ 120.1\angle{-153.3}\\ 121.5\angle{83.9} \end{bmatrix} \ \text{(V)}\]
此时所有相的电压都在规定的范围内。
例6.2说明了如何对配电网的串联元件进行建模,然后应用梯形迭代法计算潮流。该示例还说明了如何确定补偿器电路的设置,以及补偿器电路如何使各个调节器上的抽头发生变化,从而使负荷中心(节点4)的最终电压在指定的限制范围内。
负荷分配
根据变电站的计量方式,通常输入到馈线的复功率是已知的。该信息可以是三相的,也可以是单相的。在某些情况下,计量数据可以是每相中的电流和功率因数。
若期望计算得到的输入复功率与计量得到的输入复功率相吻合,可以通过计算计量得到的复功率与计算得到的复功率的比率来实现。将负荷乘以该比率来修改相负荷。因为当负荷改变时馈线的损耗也会改变,所以必须通过梯形迭代来进一步确定馈线的输入功率。这个新的输入功率将更接近计量输入功率,但很可能不在指定的允许误差范围内。同样,可以确定比率并修改负荷。重复该过程,直到计算的输入功率和计量得到的输入功率误差在的指定范围内。
负荷分配不必限于匹配变电站的计量读数。我们可以在馈线上能获得计量数据的任何位置执行相同的过程。唯一的区别是只有计量点的下游节点的负荷才能被修改。
回路电流法
分布式电源(distributed generation,DG)指接入中压、低压配电网的电源,其发电功率在几千瓦到50 MW之间。接入配电网的DG种类很多,包括光伏发电、风力发电、微型燃气轮机、燃料电池、储能设备等。
梯形迭代法
优点:运算简单、收敛性好、节省内存;
缺点:环路处理能力弱,应用于存在一定数量环路的配电网络,计算容易发散;难以处理PV节点。
为了处理PV类型的节点,目前的做法通常是根据电压和无功之间的灵敏度,在前推过程中将PV节点转化为PQ节点,但这样处理对算法的收敛性会产生多大影响目前缺乏理论分析和充分的算例验证。
配电网中一般可以忽略馈线对地电纳和变压器对地支路。当配电网处于辐射状或弱环网运行状态时,其独立环路数比节点数少得多,所以回路电流法比较适用于进行配电网潮流计算。
对配电网的图所做的规则
1)进行三相建模;2)忽略馈线对地导纳;3)大地节点和根节点之间加入等效等压源。
首先将配电网看成是由顶点和支路组成的图,图上的支路对应于馈线、变压器绕组、负荷、并联电容、电压源等设备。以 IEEE 4节点标准配电网络为例,其示意图如下所示:

网络中变压器采用三角形-三角形接法,则网络拓扑图如图:

基于回路电流法的配电网潮流基本方程
支路电流和回路电流之间的关系:
\[\begin{eqnarray} \label{666.1} {I}_{b}={B}^{\text{T}}{I}_{1} \end{eqnarray}\]式中:\({B}\)为回路矩阵,行对应回路,列对应支路。
如果将变压器原边绕组、变压器副边绕组、恒功率负荷、恒电流负荷对应的支路排在最后,则\({B}\)可以表示为:
\[\begin{eqnarray} \label{666.2} {B} = \begin{bmatrix} {B}_{\text{o}} & {B}_{\text{T1}} & {B}_{\text{T2}} & {B}_{\text{L1}} & {B}_{\text{L2}} \end{bmatrix} \end{eqnarray}\]式中:\({B}_{\text{0}}\)为馈线、恒阻抗、电容和电抗支路对应的部分;\({B}_{\text{T1}}\)为变压器原边支路对应的部分;\({B}_{\text{T2}}\)为变压器副边支路对应的部分;\({B}_{\text{L1}}\)为恒功率负荷支路对应的部分;\({B}_{\text{L2}}\)为恒电流负荷支路对应的部分。图中支路编号已经按照此顺序进行排列。
IEEE 4节点标准配电网网络的回路矩阵
设定支路电流的正方向:
馈线对应支路的正方向:编号小的节点流向编号大的节点;
变压器绕组和负荷对应的支路:正方向如第4章中所示。
此时IEEE4节点 标准配电网对应的回路矩阵为

基于回路电流法的配电网潮流基本方程的推导
配电网络中一般只有电压源,基尔霍夫电压定律(KVL)的矩阵形式为:
\[\begin{eqnarray} \label{666.3} {BZB}^{\text{T}}{I}_{1}-{BU}_{\text{s}}=0 \end{eqnarray}\]式中:\({Z}\)为阻抗矩阵;\({U}_{\text{s}}\)为电压源复向量。\({U}_{\text{s}}\)可以表示为:
\[\begin{eqnarray} \label{666.4} {U}_{\text{s}}=\begin{bmatrix} {U}_{\text{o}}^{\text{T}} & -{U}_{\text{T1}}^{\text{T}} & {U}_{\text{T2}}^{\text{T}} & -{U}_{\text{L1}}^{\text{T}} & -{U}_{\text{L2}}^{\text{T}} \end{bmatrix} ^{\text{T}} \end{eqnarray}\]式中:\({U}_{\text{o}}\)为对应电压源电压复向量,值为常数;\({U}_{\text{T1}}\)为变压器原边支路对应的电压复向量;\({U}_{\text{T2}}\)为变压器副边绕组对应的电压复向量;\({U}_{\text{L1}}\)为恒功率负荷支路对应的电压复向量;\({U}_{\text{L2}}\)为恒电流阻抗支路对应的电压复向量。
\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\)正方向与电流正方向相同,\({U}_{\text{T2}}\)正方向和电流正方向相反,故只有\({U}_{\text{T2}}\)前面是正号,其余均加上负号。
\({U}_{\text{T1}}\)和\({U}_{\text{T2}}\)之间有如下关系:
\[\begin{eqnarray} \label{666.5} {U}_{\text{T2}}={N}_{\text{T1}}{U}_{\text{T1}} \end{eqnarray}\]式中:\({N}_{\text{T1}}\)为常数方阵,采用有名值计算时数值为原副边匝数比的倒数,采用标幺值计算时数值均为1。
将下面两个式子带入最上面的式子,可得:
\[\begin{eqnarray} \label{666.6} {BZB}^{\text{T}}{I}_{1}+({B}_{\text{T1}}-{B}_{\text{T2}}{N}_{\text{T1}}){U}_{\text{T1}}+{B}_{\text{L1}}{U}_{\text{L1}}+{B}_{\text{L2}}{U}_{\text{L2}}-{B}_{\text{o}}{U}_{\text{o}}=0 \end{eqnarray}\]将\({I}_{1}\)、\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\)作为未知量,除式上面得出来的式子之外,还需要增加相应数量的方程才能求解:
(1)变压器绕组电流关系。变压器原副边之间电流关系式为
\[\begin{eqnarray} \label{666.7} {N}_{\text{t}}{B}_{\text{T1}}^{\text{T}}{I}_{1}-{B}_{\text{T2}}^{\text{T}}{I}_{1}=0 \end{eqnarray}\]式中:\({N}_{\text{T}}\)为对角矩阵,采用有名值计算时其值为变压器匝数比,采用标幺值计算时其为单位阵。
(2)非恒阻抗负荷功率平衡方程。恒功率负荷的功率平衡方程为
\[\begin{eqnarray} \label{666.8} \text{diag}({U}_{\text{L1}}){B}_{\text{L1}}^{\text{T}}{I}_{1}^{*}-{S}_{\text{L}}=0 \end{eqnarray}\]式中:diag()表示取对角矩阵,括号内向量为对角线元素;上标“*”表示共轭;\({S}_{\text{L}}\)为负荷功率组成的常复数向量。
恒电流负荷(指电流幅值和功率因数恒定的负荷)的功率平衡方程:
\[\begin{eqnarray} \label{666.9} \text{diag}({U}_{\text{L2}}){B}_{\text{L2}}^{\text{T}}{I}_{1}^{*}-|{U}_{\text{L2}}| \cdot {I}_{\text{L2}}=0 \end{eqnarray}\]式中:\(|{U}_{\text{L2}}|\)为\({U}_{\text{L2}}\)中元素取模后组成的向量;\({I}_{\text{L2}}\)为恒电流负荷电流向量,该向量第\(k\)个元素\({I}_{\text{L2},k}\)=\(|{I}_{\text{L2},k}| \angle \phi _{\text{L2},k}\),其中\(|{I}_{\text{L2},k}|\)为该负荷电流的幅值,\(\phi _{\text{L2},k}\)为其功率因数角;“\(\cdot\)”表示2个维数相同向量取对应元素相乘得到新向量。
不包含DG的回路电流法潮流基本方程组
配电网回路电流法基本方程组:
\[\begin{eqnarray} \label{zmta} {BZB}^{\text{T}}{I}_{1}+({B}_{\text{T1}}-{B}_{\text{T2}}{N}_{\text{T1}}){U}_{\text{T1}}+{B}_{\text{L1}}{U}_{\text{L1}}+{B}_{\text{L2}}{U}_{\text{L2}}-{B}_{\text{o}}{U}_{\text{o}}=0 \end{eqnarray}\] \[\begin{eqnarray} \label{zmtb} {N}_{\text{t}}{B}_{\text{T1}}^{\text{T}}{I}_{1}-{B}_{\text{T2}}^{\text{T}}{I}_{1}=0 \end{eqnarray}\] \[\begin{eqnarray} \label{zmtc} \text{diag}({U}_{\text{L1}}){B}_{\text{L1}}^{\text{T}}{I}_{1}^{*}-{S}_{\text{L}}=0 \end{eqnarray}\] \[\begin{eqnarray} \label{zmtd} \text{diag}({U}_{\text{L2}}){B}_{\text{L2}}^{\text{T}}{I}_{1}^{*}-|{U}_{\text{L2}}| \cdot {I}_{\text{L2}}=0 \end{eqnarray}\]状态变量为:
\({I}_{1}\)、\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\)
将方程中所有复数矩阵(\({I}_{1}\)、\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\)、\({Z}\))的实部和虚部分开,以\({I}_{1}\)、\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\)的实部和虚部作为未知量,使用牛拉法求解,可得Jacobian矩阵的形式如:
\[\begin{eqnarray} \label{666.10} {J}_{ac}=[{J}_{\text{ac},1},{J}_{\text{AC},2}] \end{eqnarray}\]其中:
\[\begin{equation} [{J}_{\text{ac},1}]= \begin{bmatrix} {BZ}^{x}{B}^{\text{T}} & -{BZ}^{y}{B}^{\text{T}} & {B}_{\text{T1}}-{B}_{\text{T2}}{N}_{\text{T1}} & 0 \\ {BZ}^{y}{B}^{\text{T}} & {BZ}^{x}{B}^{\text{T}} & 0 & {B}_{\text{T1}}-{B}_{\text{T2}}{N}_{\text{T1}} \\ {N}_{\text{t}}{B}_{\text{T1}}^{\text{T}}-{B}_{\text{T2}}^{\text{T}} & 0 & 0 & 0 \\ 0 & {N}_{\text{t}}{B}_{\text{T1}}^{\text{T}}-{B}_{\text{T2}}^{\text{T}} & 0 & 0 \\ \text{diag}({U}_{\text{L1}}^{x}){B}_{\text{L1}}^{\text{T}} & \text{diag}({U}_{\text{L1}}^{y}){B}_{\text{L1}}^{\text{T}} & 0 & 0 \\ \text{diag}({U}_{\text{L1}}^{y}){B}_{\text{L1}}^{\text{T}} & -\text{diag}({U}_{\text{L1}}^{x}){B}_{\text{L1}}^{\text{T}} & 0 & 0 \\ \text{diag}({U}_{\text{L2}}^{x}){B}_{\text{L2}}^{\text{T}} & \text{diag}({U}_{\text{L2}}^{y}){B}_{\text{L2}}^{\text{T}} & 0 & 0 \\ \text{diag}({U}_{\text{L2}}^{y}){B}_{\text{L2}}^{\text{T}} & -\text{diag}({U}_{\text{L2}}^{x}){B}_{\text{L2}}^{\text{T}} & 0 & 0 \end{bmatrix} \end{equation}\]
式中:上标“\(x\)”“\(y\)”分别表示复数矩阵(复向量)的实部、虚部。
IEEE 4节点网络的雅可比矩阵
智能配电网中的DG模型
PQ节点模型:
在潮流计算中,采用恒功率因数和恒功率控制方式的工频热电联产同步机组的有功和无功出力可看成恒定值,可将其作为PQ节点进行处理,本节称其为PQ节点模型。
\[\begin{eqnarray} \label{666.11} \text{diag}({U}_{\text{G1}}){B}_{\text{G1}}^{\text{T}}{I}_{1}^{*}+{S}_{\text{G1}}=0 \end{eqnarray}\]式中:\({B}_{\text{G1}}\)为回路矩阵\({B}\)中该类型DG支路对应的部分;\({U}_{\text{G1}}\)为DG支路电压复向量;\({S}_{\text{G1}}\)为DG功率组成的常复数向量。
恒电流模型:
光伏发电系统和蓄电池并网控制的是输入电网的电流,在潮流计算中可以将它们视为向电网输入电流的恒电流负荷:
\[\begin{eqnarray} \label{666.12} \text{diag}({U}_{\text{G2}}){B}_{\text{G2}}^{\text{T}}{I}_{1}^{*}+|{U}_{\text{G2}}| \cdot {I}_{\text{G2}}=0 \end{eqnarray}\]式中:\({B}_{\text{G2}}\)为\({B}\)中该类型DG支路对应的部分;\({U}_{\text{G2}}\)为DG支路电压复向量;\(|{U}_{\text{G2}}|\)表示\({U}_{\text{G2}}\)中元素取模后组成的向量;\({I}_{\text{G2}}\)为DG支路电流常复数向量。
PV节点模型:
在潮流计算中,燃料电池、微型燃气轮机、采用自动电压调节的工频热电联产同步机组的有功出力和电压幅值可看成恒定值,故可将其作为PV节点进行处理:
\[\begin{gather} \text{diag}({U}_{\text{G3}}^{x}){B}_{\text{G3}}^{\text{T}}{I}_{1}^{x}+\text{diag}({U}_{\text{G3}}^{y}){B}_{\text{G3}}^{\text{T}}{I}_{1}^{y}+{P}_{\text{G3}}=0 \label{666.13}\\ |{U}_{\text{G3}}|-{U}_{\text{FG3}}=0 \label{666.14}\end{gather}\]中:\({B}_{\text{G3}}\)为\({B}\)中该类型DG支路对应的部分;\({U}_{\text{G3}}^{x}\)、\({U}_{\text{G3}}^{y}\)分别为DG支路电压实部和虚部组成的向量;\({I}_{1}^{x}\)、\({I}_{1}^{y}\)分别为回路电流实部和虚部组成的向量;\({P}_{\text{G3}}\)、\({U}_{\text{FG3}}\)分别为DG支路有功和电压幅值常数向量。
对于以上3类DG,处理方法与非恒阻抗负荷支路是类似的,即在状态变量中增加DG支路电压,并增加相应的DG支路方程与其他方程联立求解。
异步发电机模型:
风机是一种常见的DG,它在潮流计算中常作为异步电机模型参与计算。异步电机本身没有励磁装置,主要靠电网提供的无功建立磁场,在潮流计算中既不能作为PQ节点,也不能作为PV节点,其三相有功一般是已知量,而无功是电压和转差率的函数,考虑到三相不平衡的情况,需要采用序分量进行分析。
以星形接法的三相异步电机为例,异步电机等效电路如图所示:

异步电机一般采用中性点不接地的方式,因此电机的零序电压和电流均为0。图中,\(R_{\text{s}}\)为定子电阻;\(X_{\text{s}}\)为定子漏抗;\(R_{\text{r}}\)为转子电阻;\(X_{\text{r}}\)为转子漏抗;\(X_{m}\)为励磁电抗;\({U}_{i}\)为序电压,\({I}_{i}\)为序电流,\(s_{i}\)为转差率,\(i\)=1表示正序,\(i\)=2表示负序。
正序和负序等效电路的唯一区别在于\(s_{i}\)不同,正序和负序转差率有如下关系式:
\[\begin{gather} s_{1}=\frac{n_{\text{s}}-n}{n_{\text{s}}} \label{666.15}\\ s_{2}=2-s_{1} \label{666.16}\end{gather}\]式中:\(n_{\text{s}}\)为同步转速;\(n\)为转子转速。
在潮流计算中,认为风机发出的有功功率是给定值,设为\(P\),则可得下面3个方程:
\[\begin{gather} U_{1,x}I_{1,x}+U_{1,y}I_{1,y}+U_{2,x}I_{2,x}+U_{2,y}I_{2,y}+P/3=0 \label{666.17}\\ \frac{{U}_{1}-(R_{\text{s}}+\text{j}X_{\text{s}}){I}_{1}}{\text{j}X_{m}}+\frac{{U}_{1}-(R_{\text{s}}+\text{j}X_{\text{s}}){I}_{1}}{\text{j}(R_{\text{r}}/s_{1}+\text{j}X_{\text{r}})}-{I}_{1}=0 \label{666.18}\\ \frac{{U}_{2}-(R_{\text{s}}+\text{j}X_{\text{s}}){I}_{2}}{\text{j}X_{m}}+\frac{{U}_{2}-(R_{\text{s}}+\text{j}X_{\text{s}}){I}_{2}}{\text{j}(R_{\text{r}}/s_{2}+\text{j}X_{\text{r}})}-{I}_{2}=0 \label{666.19}\end{gather}\]将上面两个式子写成实部和虚部的形式:
\[\begin{gather} \begin{split} R_{\text{r}}U_{i,x}-R_{\text{r}}R_{\text{s}}I_{i,x}+(R_{\text{r}}X_{\text{s}}+R_{\text{r}}X_{m})I_{i,y}+s_{i}[(X_{\text{s}}X_{\text{r}}+X_{\text{s}}X_{m}+X_{\text{r}}X_{m})I_{i,x}+\\ (R_{\text{s}}X_{\text{r}}+R_{\text{s}}X_{m})I_{i,y}-(X_{\text{r}}+X_{m})U_{i,y}]=0 \end{split} \label{666.20}\\ \begin{split} R_{\text{r}}U_{i,y}+R_{\text{r}}R_{\text{s}}I_{i,y}-(R_{\text{r}}X_{\text{s}}+R_{\text{r}}X_{m})I_{i,x}+s_{i}[(X_{\text{s}}X_{\text{r}}+X_{\text{s}}X_{m}-X_{\text{r}}X_{m})I_{i,y}-\\ (R_{\text{s}}X_{\text{r}}+R_{\text{s}}X_{m})I_{i,x}+(X_{\text{r}}+X_{m})U_{i,x}]=0 \end{split} \label{666.21} \end{gather}\]包含感应电机模型的回路电流法改进
基于上述方法求解含感应电机模型的配电网潮流时,需要进行如下改进:
(1)增加感应电机的正序电压、负序电压、正序转差率(下面简称转差率)作为状态变量。
(2)在回路KVL方程中\({U}_{\text{s}}\)部分,异步电机支路对应的位置增加等效电压源,其值为\(-{A}_{p1}{U}_{i,1}-{A}_{p2}{U}_{i,2}\),其中\(p\in \{1,2,3\}\)为该支路对应的相位;\({A}_{p1}\)、\({A}_{p2}\)分别为正序和负序分量到三相分量的变换矩阵;\({U}_{i,1}\)、\({U}_{i,2}\)为第\(i\)台异步电机的正序和负序电压。
(3)用回路电流表示异步电机的正序、负序电流,并代入前面5个方程中,和前面不含DG的4个回路电流法方程联立,用牛顿法进行求解。
基于回路电流法的潮流算法步骤
(1)初始化,形成配电网络详细拓扑图,从大地顶点开始广度优先遍历图,形成树枝和连枝,每一条连枝对应一个基本回路,基本回路由一条连枝和若干树枝组成(如前面IEEE4节点的拓扑图所示),根据基本回路形成回路矩阵\({B}\),设置\({I}_{1}\)、\({U}_{\text{T1}}\)、\({U}_{\text{L1}}\)、\({U}_{\text{L2}}\),以及DG支路电压和异步电机正序电压、负序电压、转差率的初值。通常电压初值为额定值,电流和转差率初值均为0,并置\(k\)=1。
(2)计算回路电流法方程组以及DG相关方程式的不平衡量,将计算结果实部和虚部依次排列组成向量并设为\(\Delta {f}\)。
(3)计算Jacobian矩阵,计算结果为\({J}_{\text{ac}}\)。
(4)通过计算\(-{J}_{\text{ac}}^{-1} \Delta {f}\),通过修正量\(\Delta {I}_{1}^{x}\)、\(\Delta {I}_{1}^{y}\)、\(\Delta {U}_{\text{T1}}^{x}\)、\(\Delta {U}_{\text{T1}}^{y}\)、\(\Delta {U}_{\text{L1}}^{x}\)、\(\Delta {U}_{\text{L1}}^{y}\)、\(\Delta {U}_{\text{L2}}^{x}\)、\(\Delta {U}_{\text{L2}}^{y}\),以及与DG相关的状态变量的修正量,并更新未知量:
\[\begin{equation} \left\{\begin{aligned} &{I}_{1}^{k+1}={I}_{1}^{k}+\Delta {I}_{1}^{x}+j\Delta {I}_{1}^{y} \\ &{U}_{\text{T1}}^{k+1}={U}_{\text{T1}}^{k}+\Delta {U}_{\text{T1}}^{x}+\text{j}\Delta {U}_{\text{T1}}^{y} \\ &{U}_{\text{L1}}^{k+1}={U}_{\text{L1}}^{k}+\Delta {U}_{\text{L1}}^{x}+\text{j}\Delta {U}_{\text{L1}}^{y} \\ &{U}_{\text{L2}}^{k+1}={U}_{\text{L2}}^{k}+\Delta {U}_{\text{L2}}^{x}+\text{j}\Delta {U}_{\text{L2}}^{y} \\ &\ \ \qquad \qquad \quad \vdots \end{aligned} \right. \label{666.22} \end{equation}\](5)判断连续2次之间的修正量绝对值是否都小于收敛标准,若是,则结束;否则令\(k=k+1\)并返回步骤2。
基于IEEE 34节点系统构造的算例
IEEE 34节点系统是根据真实的配电网络数据建立的,附录C给出了其单线图和具体参数。
【特点:】
线路很长,负荷很轻,具有并联电容,有缺相的现象;
| DG编号 | 类型 | 接入节点 | 参数 |
|---|---|---|---|
| DG1 | PQ节点 | 846 | Y接,每相额定功率30+j20 kV\(\cdot\)A |
| DG2 | 恒电流 | 836 | Y接,每相额定功率30+j20 kV\(\cdot\)A |
| DG3 | PV节点 | 860 | Y接,每相额定有功30 kW |
| DG4 | 异步发电机 | 848 | 见文献[3] T1、G1 |
| DG5 | 异步发电机 | 890 | 见文献[3] T2、G2 |
| 方案 | DG类型 | DG接入情况 |
|---|---|---|
| 1 | PQ节点 | 仅接入DG1 |
| 2 | 恒电流 | 仅接入DG2 |
| 3 | PV节点 | 仅接入DG3 |
| 4 | PQ节点+恒电流+PV节点 | 接入DG1-DG3 |
| 5 | 异步电机 | 仅接入DG4 |
| 6 | 异步电机 | 接入DG4、DG5 |
| 7 | PQ节点+恒电流+PV节点+异步电机 | 接入DG1-DG5 |
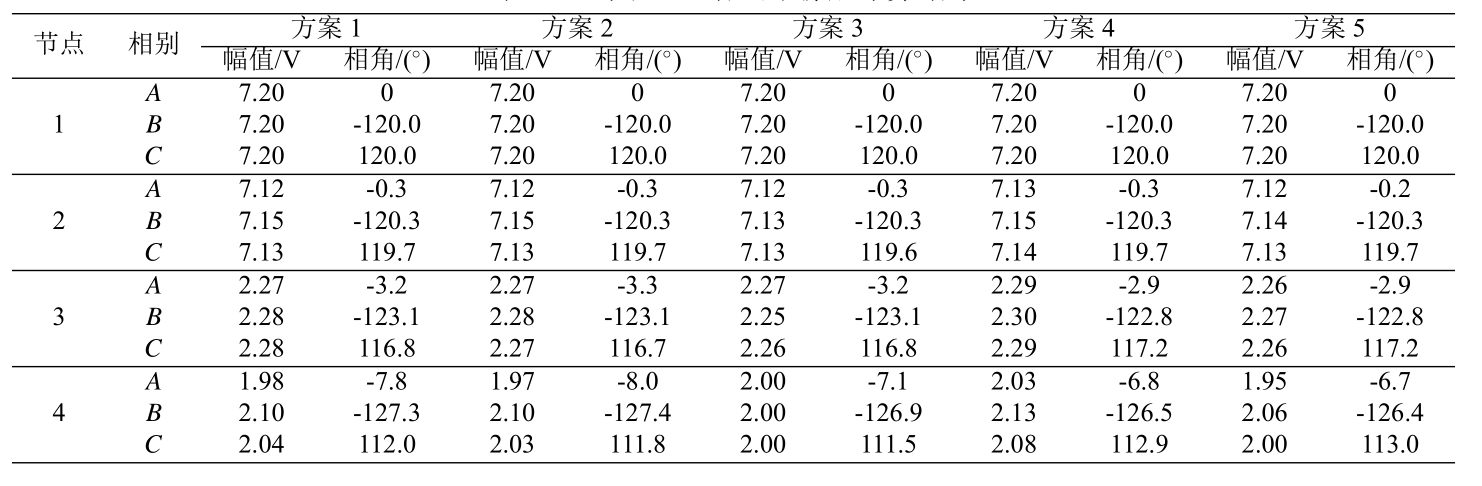
测试结果
| 梯形迭代法 | 本节方法 | 梯形迭代法 | 本节方法 |
|---|---|---|---|
| 1 | 8 | 4 | 0.235 |
| 2 | 8 | 4 | 0.234 |
| 3 | 8 | 4 | 0.206 |
| 4 | 7 | 4 | 0.223 |
| 5 | 11 | 6 | 0.344 |
| 6 | 不收敛 | 6 | —— |
| 7 | 不收敛 | 7 | —— |
在梯形迭代收敛的情况下,本节方法的迭代次数少于梯形迭代法。
在方案6中出现梯形迭代法不收敛的情况,该方案用本节方法计算能够收敛。
本节所采用的方法在梯形迭代法也收敛的情况下,比梯形迭代法计算速度更快,证明了本节算法的快速性。
为了测试算法处理环路的能力,通过合并节点增加环路的方式构造了相应算例。所谓合并是指把2个电压等级相同的节点变成一个节点,并将原来连在2个节点上的设备连到合并后的节点上。对IEEE 34节点系统,将节点822和848合并、节点826和858合并。合并后,原辐射状网络变成含2个环路的网络。
| 方案 | 本节方法迭代次数 | 方案 | 本节方法迭代次数 |
|---|---|---|---|
| 1 | 4 | 5 | 6 |
| 2 | 4 | 6 | 6 |
| 3 | 4 | 7 | 7 |
| 4 | 4 | | |
| 电机 | 正序电压 | 正序电压 | 负序电压 | 负序电压 | 转差率 |
|---|---|---|---|---|---|
| 幅值/V | 相角/(\(^{\circ}\)) | 幅值/V | 相角/(\(^{\circ}\)) | ||
| G1 | 252.64 | 6.9 | 1.13 | 123.0 | -0.00966 |
| G2 | 0.22 | 19.5 | 1.24 | 82.1 | -0.01330 |
可见本节方法在测试中收敛次数在7次之内,验证了本节方法的有效性。同时,针对配电网中DG常见的PV节点处理,方案3算例中节点836接入PV型DG,其节点电压计算结果为13.00 kV(见表),这与额定相电压相同,因此验证了本节对PV节点处理的正确性。
基于IEEE 34节点系统的弱环网测试结果见课本
课本还给出了基于IEEE 123节点系统构造的算例、基于IEEE 33节点系统构造的算例、基于IEEE 69节点系统构造的算例,同学们可以自行阅读学习。
算法特点分析与总结
本节提出了一种基于回路电流法的配电网三相潮流算法,并提出了异步电机模型等多种DG模型的处理方法,所提方法具有以下特征:
(1)本节方法采用牛顿法求解,没有对Jacobian矩阵进行简化或近似,算法具有二阶收敛性;
(2)本节方法基于回路电流法建立潮流方程,具有较强的处理环网的能力,对于辐射状和弱环状配电网不需要区别对待、环路解列以及额外的拓扑分析和复杂的节点编号;
(3)在推导过程中没有对\(R/X\)做任何假设;
(4)Jacobian矩阵中的大部分元素是恒定值,只有非恒阻抗负荷与DG对应的部分是变化的,更新Jacobian的工作量较小;
(5)本节方法能够处理恒电流、恒功率、恒阻抗等类型的负荷,也能够处理异步电机、PV节点等类型的DG,处理PV节点过程不需要将PV节点转换成PQ节点。
不受配电网三相不平衡的影响,无须确定环路解列点,解决了求解含DG智能配电网潮流的问题,通用性较强,收敛性好,迭代次数少,计算速度快,对于环路的处理能力强,并且能够处理所有常见的DG模型,在配电网潮流计算方面具有一定的优越性。
短路分析
输电网通常应用对称分量法来解决正常对称三相系统中的不对称故障的短路电流计算问题。
该方法不太适合于不对称的配电网络。相之间的相互耦合会导致序网络之间的相互耦合,当存在这种情况时,使用对称分量法没有任何优势。
基本理论
如图显示了不对称网络的短路分析模型,图中所示的任何一个点都可能发生短路。节点1是配电变电站的高压母线。节点1处的短路电流值通常由输电网短路分析确定。这些分析的结果以三相和单相短路复功率的形式提供。使用短路复功率,可以确定等效系统的正序和零序阻抗。图中其他四点的短路分析需要用到这些值。

给定三相短路复功率的幅度和角度,以欧姆为单位的正序等效系统阻抗由下式确定:

给定单相短路复功率幅度和角度,以欧姆为单位的零序等效系统阻抗由下式确定:

在上式中,\(kVLL\)是系统的额定线电压,单位为kV。计算出的正序和零序阻抗需要转换为相阻抗矩阵,在第二章我们已经提到了转换的公式。
对于第2、3、4和5点的短路,需要在短路点计算戴维南等效三相电路。戴维南等效电压是具有适当角度的额定线对地电压。例如,假设等效系统线对地电压是额定三相电压,相角为零。点2和3处的戴维南等效电压将通过将系统电压乘以变电站变压器的广义变压器矩阵\([At]\)来计算。进一步地,第4点和第5点的戴维南等效电压将是节点3的电压乘以变压器的广义矩阵\([At]\)。
戴维南等效相阻抗矩阵是系统电压源和故障点之间每个元件的相阻抗矩阵之和。假设步进电压调节器设置在中性位置,它们不会进入短路计算。对于三角形 - 接地星形变压器,变压器高压侧的总相阻抗矩阵必须使用公式(4.125)换算到低压侧。
故障节点处的戴维南等效
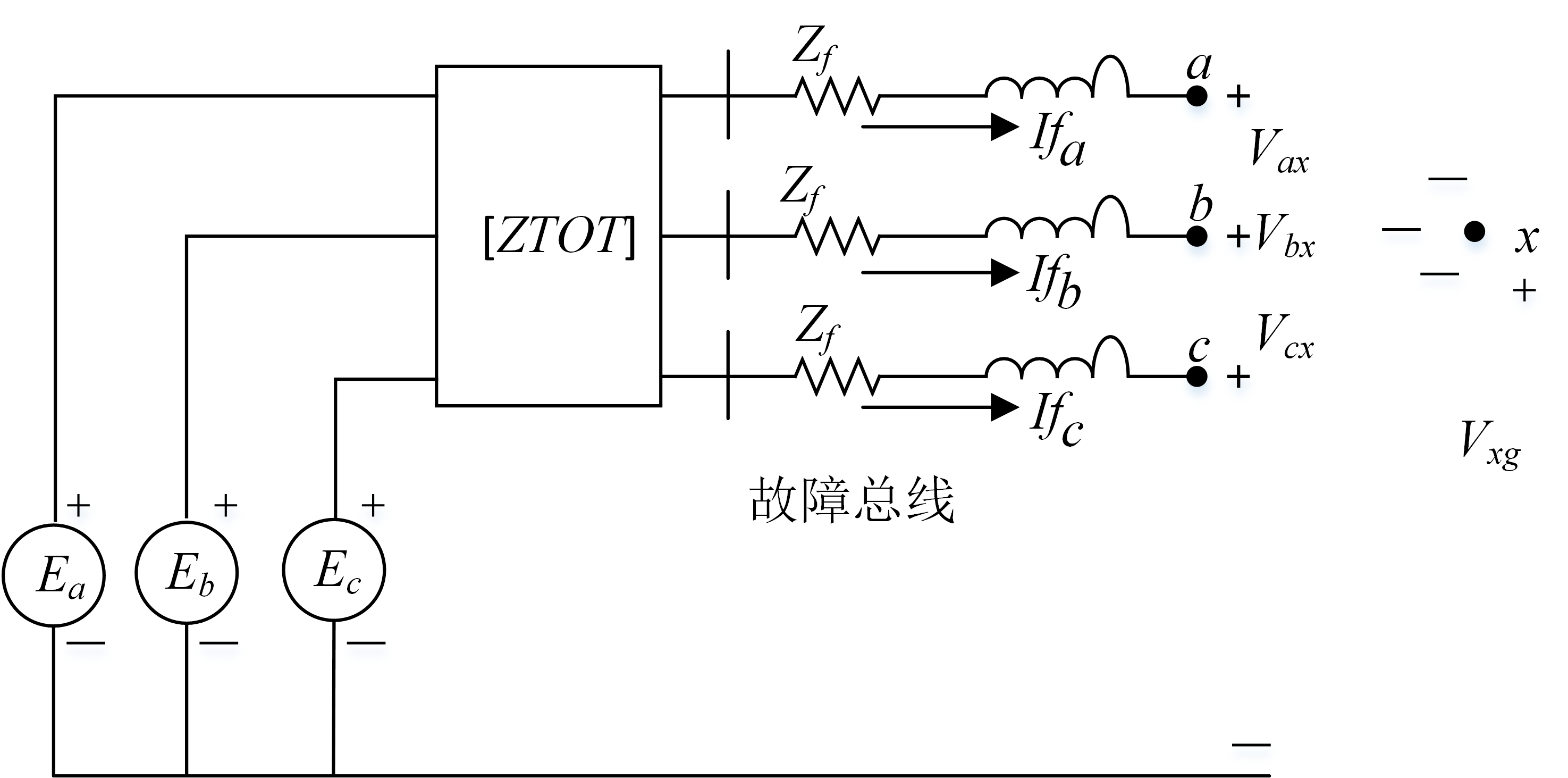
如图显示了故障节点处的戴维南等效电路。在图中,电压源\(E_{a}\),\(E_{b}\)和\(E_{c}\)表示故障节点处的戴维南等效线对地电压。 矩阵\([ZTOT]\)表示故障节点处的戴维南等效相阻抗矩阵。故障阻抗由图中的\(Z_{\text{f}}\)表示。
该图矩阵形式的基尔霍夫电压定律:
\[\begin{eqnarray} \label{c12} \begin{bmatrix} E_{a}\\ E_{b}\\ E_{c} \end{bmatrix}=\begin{bmatrix} Z_{aa} & Z_{ab} &Z_{ac} \\ Z_{ba} &Z_{bb} &Z_{bc} \\ Z_{ca} &Z_{cb} & Z_{cc} \end{bmatrix}\cdot \begin{bmatrix} If_{a}\\ If_{b}\\ If_{c} \end{bmatrix}+\begin{bmatrix} Z_{\text{f}} & 0 &0 \\ 0 &Z_{\text{f}} &0 \\ 0 & 0 & Z_{\text{f}} \end{bmatrix}\cdot \begin{bmatrix} If_{a}\\ If_{b}\\ If_{c} \end{bmatrix}+\begin{bmatrix} V_{ax}\\ V_{bx}\\ V_{cx} \end{bmatrix}+\begin{bmatrix} V_{xg}\\ V_{xg}\\ V_{xg} \end{bmatrix} \end{eqnarray}\]可以将上式简写为:
\[\begin{eqnarray} \label{c13} \left [ E_{abc} \right ]=\left [ ZTOT \right ]\cdot \left [ If_{abc} \right ]+\left [ ZF \right ]\cdot \left [ If_{abc} \right ]+\left [ V_{abcx} \right ]+\left [ V_{xg} \right ] \end{eqnarray}\]合并上式中的项,得方程(A):
\[\begin{eqnarray} \label{c14} \left [ E_{abc} \right ]=\left [ ZEQ \right ]\cdot \left [ If_{abc} \right ]+\left [ V_{abcx} \right ]+\left [ V_{xg} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{c15} \left [ ZEQ \right ]=\left [ ZTOT \right ]+\left [ ZF \right ] \end{eqnarray}\]解方程(A)的故障电流,得到式(B):
\[\begin{eqnarray} \label{c16} \left [ If_{abc} \right ]=\left [ Y \right ]\cdot \left [ E_{abc} \right ]-\left [ Y \right ]\cdot \left [ V_{abcx} \right ]-\left [ Y \right ]\cdot \left [ V_{xg} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{c17} \left [ Y \right ]=\left [ ZEQ \right ]^{-1} \end{eqnarray}\]由于矩阵\([Y]\)和\([Eabc]\)均已知,定义式(C):
\[\begin{eqnarray} \label{c18} \left [ IP_{abc} \right ]=\left [ Y \right ]\cdot \left [ E_{abc} \right ] \end{eqnarray}\]将式(C)代入式(B),得到:
\[\begin{eqnarray} \label{c19} \left [ IP_{abc} \right ]=\left [ If_{abc} \right ]+\left [ Y \right ]\cdot \left [ V_{abcx} \right ]+\left [ Y \right ]\cdot \left [ V_{xg} \right ] \end{eqnarray}\]展开上式:
\[\begin{eqnarray} \label{c20} \begin{bmatrix} IP_{a}\\ IP_{b}\\ IP_{c} \end{bmatrix}=\begin{bmatrix} If_{a}\\ If_{b}\\ If_{c} \end{bmatrix}+\begin{bmatrix} Y_{aa} & Y_{ab} &Y_{ac} \\ Y_{ba} & Y_{bb} & Y_{bc}\\ Y_{ca} & Y_{cb} & Y_{cc} \end{bmatrix}\cdot \begin{bmatrix} V_{ax}\\ V_{bx}\\ V_{cx} \end{bmatrix}+\begin{bmatrix} Y_{aa} & Y_{ab} &Y_{ac} \\ Y_{ba} & Y_{bb} & Y_{bc}\\ Y_{ca} & Y_{cb} & Y_{cc} \end{bmatrix}+ \begin{bmatrix} V_{xg}\\ V_{xg}\\ V_{xg} \end{bmatrix} \end{eqnarray}\]执行上式中的矩阵运算,得到式(D):
\[\begin{gather} IP_{a}=If_{a}+\left ( Y_{aa}\cdot V_{ax} +Y_{ab}\cdot V_{bx}+Y_{ac}\cdot V_{cx}\right )+Ys_{a}\cdot V_{xg} \notag \\ IP_{b}=If_{b}+\left ( Y_{ba}\cdot V_{ax} +Y_{bb}\cdot V_{bx}+Y_{bc}\cdot V_{cx}\right )+Ys_{b}\cdot V_{xg} \label{c21}\\ IP_{c}=If_{c}+\left ( Y_{ca}\cdot V_{ax} +Y_{cb}\cdot V_{bx}+Y_{cc}\cdot V_{cx}\right )+Ys_{c}\cdot V_{xg} \notag \end{gather}\]其中:
\[\begin{gather} Ys_{a}=Y_{aa}+Y_{ab}+Y_{ac} \notag \\ Ys_{b}=Y_{ba}+Y_{bb}+Y_{bc} \label{c22}\\ Ys_{c}=Y_{ca}+Y_{cb}+Y_{cc} \notag \end{gather}\]式(D)是用于计算所有类型短路的通用公式,其中有三个方程和七个未知数。等式中的其他三个变量(\(IP_{a}\),\(IP_{b}\)和\(IP_{c}\))是总阻抗和戴维南电压的函数,是已知的。为了求解方程(D),有必要给定四个附加的独立方程。这些方程是故障类型的函数。下面针对各种类型故障给出附加的四个等式。通过在戴维南等效图中设置短路来模拟特定类型的故障。例如,通过将节点\(a\)、\(b\)和\(c\)连接到\(x\)来模拟三相故障。这给出了三个电压方程。第四个等式来自于在节点\(x\)处应用基尔霍夫电流定律,即故障电流的总和为零。
特定短路分析
三相故障
\[\begin{gather} V_{ax}=V_{bx}=V_{cx}=0 \notag \\ I_{a}+I_{b}+I_{c}=0 \label{c23} \end{gather}\]三相接地故障:
\[\begin{eqnarray} \label{c24} V_{ax}=V_{bx}=V_{cx}=V_{xg}=0 \end{eqnarray}\]线到线故障(假设\(i\)-\(j\)故障,\(k\)相无故障):
\[\begin{gather} V_{i\text{x}}=V_{j\text{x}}=0 \notag \\ If_{k}=0 \label{c25}\\ If_{i}+If_{j}=0 \notag \end{gather}\]线对地故障(假设\(k\)相故障,\(i\)相和\(j\)相无故障):
\[\begin{gather} V_{k\text{x}}=V_{xg}=0 \notag \\ If_{i}=If_{j}=0 \label{c26} \end{gather}\]求解方法
求解七个方程的较好方法是将其写为矩阵形式,得到式(E):
\[\begin{eqnarray} \label{c27} \begin{bmatrix} IP_{a}\\ IP_{b}\\ IP_{c}\\ 0\\ 0\\ 0\\ 0 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 & Y_{1,1} & Y_{1,2} & Y_{1,3} &Y_{\text{S1}} \\ 0& 1 &0 & Y_{2,1} & Y_{2,2} & Y_{2,3} &Y_{\text{S2}} \\ 0 & 0 & 1 & Y_{3,1} & Y_{3,3} & Y_{3,3} &Y_{\text{S3}} \\ - & - &- & - &- & - &- \\ - & - & - & - & - & - & -\\ - &- & - & - & - &- &- \\ - & - & - & - & - & - & - \end{bmatrix}\cdot \begin{bmatrix} If_{a}\\ If_{b}\\ If_{c}\\ V_{ax}\\ V_{bx}\\ V_{cx}\\ V_{xg} \end{bmatrix} \end{eqnarray}\]将式上式简写为:
\[\begin{eqnarray} \label{c28} \left [ IP_{\text{s}} \right ]=\left [ C \right ]\cdot \left [ X \right ] \end{eqnarray}\]求解上式中矩阵\([X]\)内的未知数:
\[\begin{eqnarray} \label{c29} \left [ X \right ]=\left [ C \right ]^{-1}\cdot \left [ IP_{\text{s}} \right ] \end{eqnarray}\]式(E)中系数矩阵的最后四行中的空白用已知变量填充,具体取决于要模拟的故障类型。 例如,模拟三相故障的矩阵\([C]\)中的元素将是:
\[\begin{gather*} C_{4,4}=1,C_{5,5}=1,C_{6,6}=1\\ C_{7,1}=C_{7,2}=C_{7,3}=1 \end{gather*}\]最后四行中的所有其他元素设置为零。
例题三
【例题6.3】 使用例6.2的系统计算节点4的相\(a\)和\(b\)之间(\(Z_{\text{f}} = 0\))的线到线故障的短路电流。
无穷大母线的对称线电压为12.47 kV,则相电压为7.2 kV的对称电压。
\[\begin{gather*} \left [ ELL_{\text{s}} \right ]=\begin{bmatrix} 12470\angle{30}\\ 12470\angle{-90}\\ 12470\angle{150} \end{bmatrix} \ \text{V}\\ \left [ ELN_{\text{s}} \right ]=\begin{bmatrix} 7199.6\angle{0}\\ 7199.6\angle{-120}\\ 7199.6\angle{120} \end{bmatrix} \ \text{V} \end{gather*}\]节点4的线到中性点戴维南等效电压为
\[\left [ Eth_{4} \right ]=\left [ A_{\text{t}} \right ]\cdot \left [ ELN_{\text{s}} \right ]=\begin{bmatrix} 2400\angle{-30}\\ 2400\angle{-150}\\ 2400\angle{90} \end{bmatrix} \ \text{(V)}\]
变压器低压端(节点3)处的戴维南等效阻抗由线路阻抗加上变压器阻抗组成。
\[\begin{gather*} \left [ Zth_{3} \right ]=\left [ A_{\text{t}} \right ]\cdot \left [ ZeqS_{ABC} \right ]\cdot \left [ d_{\text{t}} \right ]+\left [ Zt_{abc} \right ]\\ \left [ Zth_{3} \right ]=\begin{bmatrix} 0.0366+\text{j}0.1921 & -0.0039-\text{j}0.0086 &-0.0039-\text{j}0.0106 \\ -0.0039-\text{j}0.0086 & 0.0366+\text{j}0.1886 &-0.0039-\text{j}0.0071 \\ -0.0039-\text{j}0.0106 & -0.0039-\text{j}0.0071 & 0.0366+\text{j}0.1906 \end{bmatrix} \ \Omega \end{gather*}\]注意,戴维南阻抗矩阵不对称。节点4处的总戴维南阻抗为:
\[\begin{gather*} \left [ Zth_{4} \right ]=\left [ ZTOT \right ]=\left [ Zth_{3} \right ]+\left [ ZeqL_{abc} \right ]\\ \left [ ZTOT \right ]=\begin{bmatrix} 0.2273+\text{j}0.6955 & 0.0568+\text{j}0.2216 &0.0559+\text{j}0.1645 \\ 0.0568+\text{j}0.2216 & 0.2305+\text{j}0.6771 &0.0575+\text{j}0.1860 \\ 0.0559+\text{j}0.1645 & 0.0575+\text{j}0.1860 & 0.2287+\text{j}0.6876 \end{bmatrix} \ \Omega \end{gather*}\]节点4处的等效导纳矩阵为:
\[\left [ Yeq_{4} \right ]=\left [ ZTOT \right ]^{-1}\]
得到故障点的等效注入电流为:
\[\left [ IP \right ]=\left [ Yeq_{4} \right ]\cdot \left [ Eth_{4} \right ]=\begin{bmatrix} 4466.8\angle{-96.4}\\ 4878.9\angle{138.0}\\ 4440.9\angle{16.4} \end{bmatrix} \ \text{(A)}\]
等效导纳矩阵的每一行的总和根据前式计算:
\[Y_{i}=\sum_{k=1}^{3}Yeq_{i,k}=\begin{bmatrix} 0.2580-\text{j}0.8353\\ 0.2590-\text{j}0.8240\\ 0.3007-\text{j}0.8889 \end{bmatrix} \ \text{(S)}\]
对于节点4处的\(a\)-\(b\)故障,根据线到线故障的公式有:
\[\begin{gather*} If_{a}+If_{b}=0\\ I_{c}=0\\ V_{ax}=0\\ V_{bx}=0 \end{gather*}\]利用式(E)计算系数矩阵\([C]\):

注入电流矩阵为:
\[\left [ IP_{\text{s}} \right ]=\begin{bmatrix} 4466.8\angle{-96.4}\\ 4878.9\angle{138.0}\\ 4440.9\angle{16.4}\\ 0\\ 0\\ 0\\ 0 \end{bmatrix}\ \text{A}\]
未知数的计算方法如下:
\[\left [ X \right ]=\left [ C \right ]^{-1}\cdot \left [ IP_{\text{s}} \right ]=\begin{bmatrix} 8901.7\angle{-8.4}\\ 8901.7\angle{171.6}\\ 0\\ 7740.4\angle{-90.6}\\ 0\\ 0\\ 2587.9\angle{89.1} \end{bmatrix}\]
解得
\[\begin{gather*} If_{a}=X_{1}=8901.7\angle{-8.4}\ \text{(A)}\\ If_{b}=X_{2}=8901.7\angle{171.6}\ \text{(A)}\\ If_{c}=X_{3}=0\ \text{(A)} \end{gather*}\]计算节点4处的线对地电压和短路电流,通过广义矩阵可以检查这些结果的正确性。 节点4的线对地电压是:
\[\left [ VLG_{4} \right ]=\begin{bmatrix} V_{ax}+V_{xg}\\ V_{bx}+V_{xg}\\ V_{cx}+V_{xg} \end{bmatrix}=\begin{bmatrix} 5153.4\angle{-90.4}\\ 2587.2\angle{89.1}\\ 2587.2\angle{89.1} \end{bmatrix} \ \text{(V)}\]
矩阵形式的短路电流为:
\[I_{4}=I_{3}=\begin{bmatrix} 8901.7\angle{-8.4}\\ 8901.7\angle{171.6}\\ 0 \end{bmatrix} \ \text{(A)}\]
节点3的线对地电压为:
\[\left [ VLG_{3} \right ]=\left [ a_{2} \right ]\cdot \left [ VLG_{4} \right ]+\left [ b_{1} \right ]\cdot \left [ I_{4} \right ]=\begin{bmatrix} 3261.1\angle{-63.4}\\ 1544.3\angle{161.7}\\ 2430.9\angle{89.9} \end{bmatrix} \ \text{(V)}\]
变压器高压端(节点2)的等效线电压和线电流为:
\[\begin{gather*} \left [ VLN_{2} \right ]=\left [ a_{\text{t}} \right ]\cdot \left [ VLG_{3} \right ]+\left [ b_{\text{t}} \right ]\cdot \left [ I_{3} \right ]=\begin{bmatrix} 6766.3\angle{-6.4}\\ 6833.7\angle{-119.6}\\ 7480.3\angle{116.6} \end{bmatrix} \ \text{(V)}\\ \left [I_{2} \right ]=\left [ d_{\text{t}} \right ]\cdot \left [ I_{3} \right ]=\begin{bmatrix} 3426.4\angle{-8.4}\\ 1713.2\angle{171.6}\\ 1713.2\angle{171.6} \end{bmatrix} \ \text{(A)} \end{gather*}\]最后计算无穷大母线上的等效线电压:
\[\left [VLN_{1} \right ]=\left [ a_{1} \right ]\cdot \left [ VLN_{2} \right ]+\left [ b_{1} \right ]\cdot \left [ I_{2} \right ]=\begin{bmatrix} 7199.6\angle{0}\\ 7199.6\angle{-120}\\ 7199.6\angle{120} \end{bmatrix} \ \text{(V)}\]
参考文献
- 董树锋, 章杜锡, 周飞, 等. 一种基于回路电流法的有源配电网潮流算法[J]. 电力自动化设备, 2018, 38(2): 9-17.
- Kersting W H. Distribution system modeling and analysis[M]. New York: CRC Press, 2002.
- Dugan R C, Kersting W H. Induction machine test case for the 34-bus test feeder-description[C]. Power Engineering Society General Meeting, 2006: 1-15.
- 车仁飞, 李仁俊. 一种少环配电网三相潮流计算新方法[J]. 中国电机工程学报, 2003, 23(1): 74-79.
- 吴文传, 张伯明. 配电网潮流回路分析法[J]. 中国电机工程学报, 2004, 24(3): 67-71.
- 李红伟, 张安安. 含PV型分布式电源的弱环配电网三相潮流计算[J]. 中国电机工程学报, 2012, 32(4): 128-135.