本次课内容

问题1:有一个打印机，但是有很多的文件需要打印，那么这些任务必然要排队等候打印机逐步的处理。这里就产生了一个问题。原则上说先来的先处理，但是有一个文件100页，它排在另一个1页的文件的前面，那么可能我们要先打印这个1页的文件比较合理。

问题2在多用户环境中，操作系统调度程序必须决定在若干进程中运行哪个程序。其中一种算法是使用队列，开始时进程放在队列的末尾，调度程序将反复提取并运行队列中的第一个进程，直到该进程运行完毕，或者并未运行完毕但时间片已用完，则把它放到队列的末尾。考虑到一些很短的进程要一味等待运行，这种方法并不太合适。一般说来，短的进程要尽可能快的结束，因此这些短进程应该拥有优先权。此外，有些进程虽然不短但非常重要，它们也应该拥有优先权。

因此为了解决这一类的问题，提出了优先队列的模型。

基本概念的基本概念

优先队列是一个至少能够提供插入（insert）和删除最小（delete_min）这两种操作的数据结构。对应于队列的操作，insert相当于queue_in，delete_min相当于queue_out。

简单实现

一个简单实现：可以用链表在表头以\(O(1)\)执行插入操作，并遍历该列表以删除最小元，这又需要\(O(N)\)的时间。

另一种方法是，始终让表保持排序状态；这使得插入代价高昂（\(O(N)\)）而delete_min花费低廉（\(O(1)\)）。由于delete_min的操作次数从不多于插入操作次数，前者是更好的想法。

还有一种实现优先队列的方法是使用二叉查找树，它对这两种操作的平均运行时间都是\(O(\log N)\)。

二叉堆（Binary Heap）

使用完全二叉树实现的堆叫做二叉堆（binary heap），这是优先队列的普遍使用于实现，所以当堆（heap）这个词不加修饰地使用时一般都是指该数据结构的这种实现。

完全二叉树是一个很整齐的结构，因此可以不用指针而只用数组来表示一颗完全二叉树。

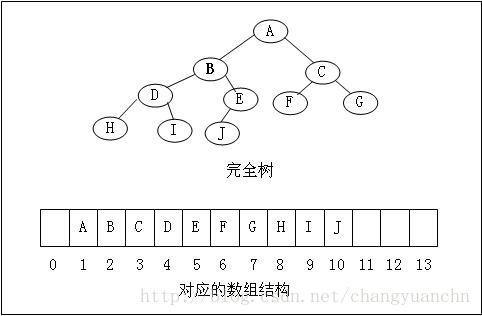
数组表示的完全二叉树

完全二叉树与数组的对应关系:

堆序性质

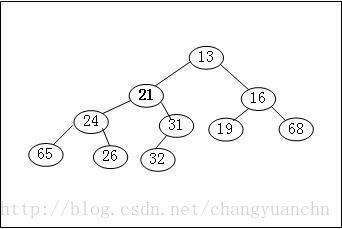
堆的顺序性质是指最小的结点应该是根节点，这是使操作快速执行的关键。如果我们考虑任意子树也应该是一个堆，那么任意节点就应该小于它的所有后裔。

应用这个逻辑，我们得到堆序性质：在一个堆中，对于每一个节点\(X\)，\(X\)的父亲中的关键字小于或等于\(X\)中的关键字，根节点除外（没有父亲）。

堆数据结构

完全二叉树实现不需要指针，就连遍历该树所需要的操作也极简单，在大部分计算机上运行都可以非常快。这种实现方法的唯一问题在于，最大的堆大小需要事先估计，但对于典型的情况这并不成问题。

因此，一个堆数据结构将由一个数组（不论关键字是什么类型）、一个代表最大值的整数以及当前的堆大小组成。

typedef struct HeapStruct;  
typedef struct HeapStruct *Heap;  
  
struct HeapStruct {  
    int capacity;  
    int size;  
    ElementType *elements;  
}

堆的插入

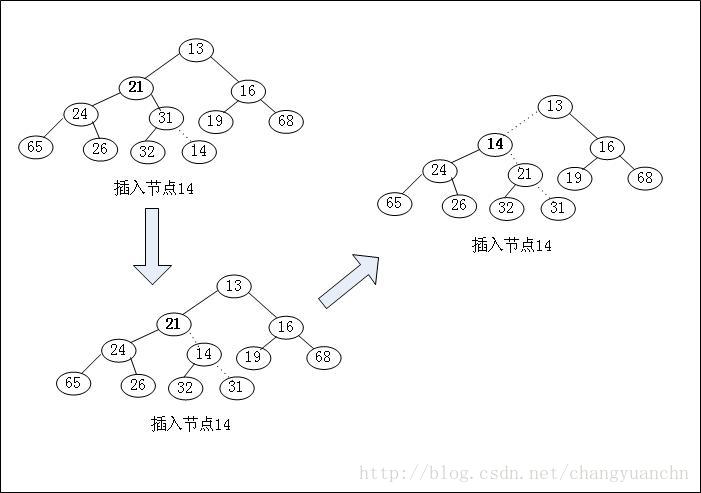
堆的插入是按照顺序插入到底层的结点上，然后与他的父节点比较，如果小于父节点，那么此结点与父节点交换位置，否则，这个位置就是应该插入的位置，依次循环。

堆插入的代码

（1）在下一个空闲位置创建一个空穴；

（2）如果\(x\)可以放在该空穴中而不破坏堆的序，那么插入完成，否则就把空穴的父节点上的元素移入该空穴中；

（3）继续上述过程直到\(x\)能被放入空穴为止。

void heap_insert(ElementType x, Heap h) {
    int i;  
    if(heap_is_full(h)) {  
        printf("Heap is Full");  
        return;
    }  
    for(i=++h->size; h->elements[i/2]>x; i/=2)  
        h->elements[i] = h->elements[i/2];  
    h->elements[i] = x;  
}

插入就是一个比较节点和父节点的过程

注意：对于堆\(h->elements[i/2]\)就是父节点。

堆的删除最小操作

找出最小元是容易的，困难的是删除它。可以用插入的思想把一步一步的向上渗透。先选取根节点的最小子节点，然后把这个这点迁移到根节点。然后递归操作。

对于删除最小操作，可与预见的是他的最坏时间复杂度为O(logN)，因为删除节点后的渗透是沿着子树走的，类似于二叉查找树的操作，故为O(logN)。

堆的删除最小操作的图示

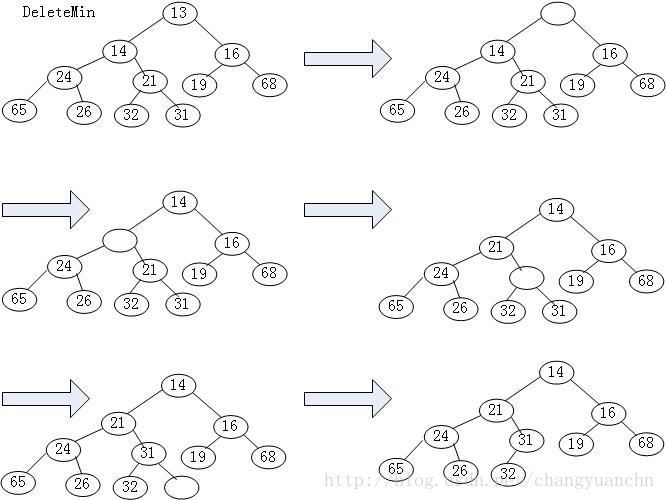
堆的删除最小操作的实现的要点

需要判断：

• 在堆的实现中经常发生的错误是当堆中存在偶数个元素的时候，此时遇到一个节点只有一个儿子的情况。
• 是否到达底层，因为对每一片树叶算法将需要一个标记。

堆的应用：堆排序

若在输出堆顶的最小值之后，使得剩余\(n-1\)个元素的序列重又建成一个堆，则得到\(n\)个元素中的次小值。如此反复执行，便能得到一个有序序列，这个过程称之为堆排序。

堆排序分析

堆排序方法对记录数较少的文件并不值得提倡，但对\(n\)较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。对深度为\(k\)的堆，筛选算法中进行的关键字比较次数至多为\(2(k-1)\)次，则在建含\(n\)个元素、深度为\(h\)的堆时，总共进行的关键字比较次数不超过\(4n\)。又，\(n\)个节点的完全二叉树的深度为\(\lfloor \log_2 n \rfloor+1\)，则调整建新堆时调用HeapAdjust过程\(n-1\)次，总共进行的比较次数不超过下式之值：

\[ 2(\lfloor \log_2(n-1) \rfloor+\lfloor \log_2(n-2) \rfloor+...+\lfloor \log_22 \rfloor<\lfloor \log_2n \rfloor) \]

由此，堆排序在最坏的情况下，其时间复杂度也为\(O(n\log n)\)。相对于快速排序来说，这是堆排序的最大优点。此外，堆排序仅需一个记录大小供交换用的辅助存储空间。