数据结构与算法

树与查找

2017年春

本次课内容

查找是二叉树的一个重要应用。本章我们介绍一种变化的数据结构二叉查找树（Binary Sort Tree），对于长的指令序列它对每种操作的运行时间基本上是\(O(\log N)\)。

在二叉排序树的基础上，本章还要介绍二叉平衡树、红黑树和B-树等常用于查找的数据结构。

二叉排序树定义

定义

二叉排序树（Binary Sort Tree）或者是一棵空树；或者是具有下列性质（简称BST性质）的二叉树：

1.若左子树不空，则左子树上所有结点的值均小于根结点的值；

2.若右子树不空，则右子树上所有结点的值均大于根结点的值；

3.左右子树也都是二叉排序树。

二叉排序树定义图示

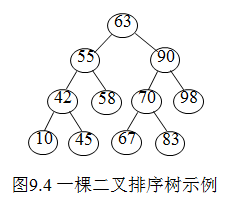
这是一张图片

由上图可以看出，对二叉排序树进行中序遍历，便可得到一个按关键字有序的序列 \[10,42,45,55,58,63,67,70,83,90,98\] 因此，一个无序序列可通过构造一棵二叉排序树而成为有序序列。

二叉排序树中查找过程

查找过程

从其定义可见，二叉排序树的查找过程为：

① 若查找树为空，查找失败；

② 查找树非空，将给定值kx与查找树的根结点关键字比较；

③ 若相等，查找成功，结束查找过程，否则，

a．当kx小于根结点关键字，查找将在左子树上继续进行，转①

b．当kx大于根结点关键字，查找将在右子树上继续进行，转①

二叉排序树查找算法

二叉排序树中查找元素的算法：

BsTreeNode *bstree_lookup_node(BsTree *tree, BsTreeKey key) {
    BsTreeNode *node;
    int diff;
    /* 搜索二叉查找树并且寻找含有特定关键字的节点 */
    node = tree->base.rootnode;
    while (node != NULL) {
        diff = tree->compareFunc(key, node->key);
        if (diff == 0) 
            return node;    /* 关键字相同则返回 */
        else if (diff < 0)
            node = node->base.children[BITREE_NODE_LEFT];
        else
            node = node->base.children[BITREE_NODE_RIGHT];
    }
    return NULL;    /* 未找到 */
}

二叉排序树查找算法分析

注意测试的顺序：

关键的问题是首先要对是否为空树进行测试，否则就可能在\(NULL\)指针上兜圈子。
其余的测试应该使得最不可能的情况安排在最后进行。

递归的使用在这里是合理的，因为算法表达式的简明性是以速度的降低为代价的，而这里所使用的栈空间的量也只不过是\(O(\log N)\)而已。

找最小值和最大值

BsTreeNode *bstree_find_min(BsTreeNode *node) {
    if(node != NULL)
        while(node->base.children[BITREE_NODE_LEFT] != NULL) 
            node = node->base.children[BITREE_NODE_LEFT];
    return node;
}   

BsTreeNode *bstree_find_max(BsTreeNode *node) {
    if(node == NULL)
        return NULL;
    else
        if(node->base.children[BITREE_NODE_RIGHT] == NULL)
            return node;
        else
            return bstree_find_max(node->base.children[BITREE_NODE_RIGHT]);
}

二查排序树插入算法思路

先讨论向二叉排序树中插入一个结点的过程：设待插入结点的关键字为kx，为将其插入，先要在二叉排序树中进行查找，若查找成功，按二叉排序树定义，待插入结点已存在，不用插入；若查找不成功，则插入之。因此，新插入结点一定是作为叶子结点添加上去的。

在二叉排序树中插入新结点，只要保证插入后仍符合二叉排序树的定义即可：

(1)若二叉排序树为空，则待插入结点*s作为根结点插入到空树中；

(2)当二叉排序树非空时，将待插结点的关键字s->key和树根的关键字t->key比较，若s->key＝ t->key，无须插入；

若s->key< t->key，则将待插结点*s插入到根的左子树中；

若s->key> t->key，则将*s插入到根的右子树中；

(3)插入子树的过程相同。

二叉查找树插入算法

将新结点 *s 插入到 t 所指的二叉排序树中的算法：

BsTreeNode *bstree_insert(BsTree *tree, BsTreeKey key, BiTreeValue value) {
    BsTreeNode **rover;
    BsTreeNode *newnode;
    BsTreeNode *previousnode;   
    /* 遍历二叉查找树，一直到空指针处 */
    rover = &(((BiTree *)tree)->rootnode);
    previousnode = NULL;
    while (*rover != NULL) {
        previousnode = *rover;
        if (tree->compareFunc(key, (*rover)->key) < 0)
            rover = &((*rover)->base.children[BITREE_NODE_LEFT]);
        else
            rover = &((*rover)->base.children[BITREE_NODE_RIGHT]);
    }
    /* 创建一个新节点，以遍历的路径上最后一个节点为双亲节点 */
    newnode = (BsTreeNode *)malloc(sizeof(BsTreeNode));
    if (newnode == NULL)
        return NULL;
    newnode->base.children[BITREE_NODE_LEFT] = NULL;
    newnode->base.children[BITREE_NODE_RIGHT] = NULL;
    newnode->base.parent = previousnode;
    newnode->base.value = value;
    newnode->key = key;
    *rover = newnode;   /* 在遍历到达的空指针处插入节点 */
    ++tree->base.nodenum;   /* 更新节点数 */
    return newnode;
}

生成一课二叉排序树的过程

构造一棵二叉排序树则是逐个插入结点的过程。

[例2]记录的关键字序列为：63，90，70，55，67，42，98，83，10，45，58，则构造一棵二叉排序树的过程如图9.5所示。

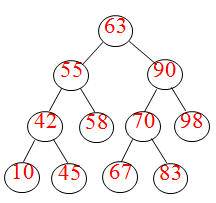
这是一张图片

二叉排序树生成算法的测试

生成二叉排序树的算法：

void test_bs_tree_new() {
    int keys[] = {63, 90, 70, 55, 67, 42, 98, 83, 10, 45, 58};
    int values[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11};
    int i, n = 11;

    BsTree *tree = bs_tree_new((BsTreeCompareFunc) int_compare);

    assert(tree != NULL);
    assert(((BiTree *)tree)->root_node(tree) == NULL);
    assert(((BiTree *)tree)->nodeNum == 0);
    /*插入一些数据*/
    for(i = 0; i < n; i++)
        tree->insert_key_value(tree, &keys[i], &values[i]);
    /*开始验证*/
    for(i = 0; i < n; i++) {
        int v = *(int *)(tree->lookup_value(tree, &keys[i]));
        assert(v == values[i]);
    }
    print_tree(((BiTree *)tree)->root_node(tree), 0);
    ((BiTree *)tree)->free_tree(tree);
}

二叉排序树插入的实际问题

重复元的插入可以通过在节点记录中保留一个附加域以指示发生的频率来处理。这使得整个树增加了某些附加空间，但却比将重复信息放到树中要好（它将使树的深度变得很大）。

如果关键字只是一个更大结构的一部分，那么这种方法行不通，此时我们可以把具有相同关键字的所有结构保留在一个辅助数据结构中，如表或是另一棵查找树中。

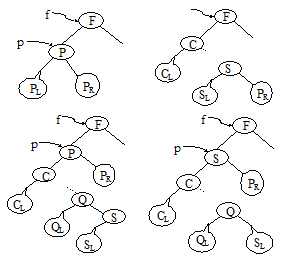
二叉排序树删除操作情况一

和许多数据结构一样，最困难的操作是删除。从二叉排序树中删除一个结点之后，需要使其仍能保持二叉排序树的特性，因此一旦发现要被删除的节点，我们就需要考虑几种可能的情况。

设待删结点为*p（p为指向待删结点的指针），PL和PR分别表示其左子树和右子树。

其双亲结点为*f，且不失一般性，可设\(*p\)是\(*f\)的左孩子。以下分三种情况进行讨论。

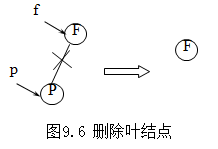
情况一：*p结点为叶结点，由于删去叶结点后不影响整棵树的特性，所以，只需将被删结点的双亲结点相应指针域改为空指针。如图9.6。

这是一张图片

二叉排序树删除操作情况二

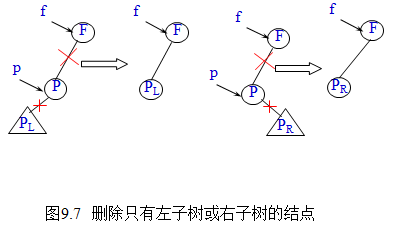
情况二：\(*p\)结点只有右子树PR　或只有左子树PL,此时，只需将PR或PL替换\(*f\)结点的\(*p\)子树即可。如图9.7。

这是一张图片

二叉排序树删除操作情况三

情况三：若\(*p\)结点的左子树和右子树均不空，删去\(*p\)时应考虑将\(*p\)的左、右子树链接到合适的位置，并保持二叉排序树的特性。先中序遍历PL后得到最后一个结点\(*s\)，其值在PL中为最大，它的右子树为空。然后有两种做法：其一是令\(*p\)的左子树为\(*f\)的左子树，而\(*p\)的右子树为\(*s\)的右子树；其二是令\(*s\)的左子树SL为\(*s\)的双亲的右子树，将\(*s\)结点取代被删除的\(*p\)结点。如图9.8所示。

这是一张图片

二叉排序树删除操作算法实现

int bstree_remove_by_key(BsTree *_this, BsTreeKey key) {
    BsTreeNode *node, *tmpcell; 
    node = bstree_lookup_node(_this, key);
    int keyvalue;
    if(node != NULL) {
        /* 两个孩子节点 */
        if(node->base.children[BITREE_NODE_LEFT] != NULL &&
                node->base.children[BITREE_NODE_RIGHT] != NULL) {
            /* 用右子树的最小节点替换 */
            tmpcell = bstree_find_min(node->base.children[BITREE_NODE_RIGHT]);
            keyvalue = *((int *)tmpcell->key);
            bstree_remove_by_key (_this, tmpcell->key);
            node->key = &keyvalue;
        }
        else {  /* 有一个或无孩子节点 */
            if(node->base.children[BITREE_NODE_LEFT] == NULL) {
                /* 判断node是左孩子还是右孩子节点指针 */
                if(int_compare(((BsTreeNode *)node->base.parent)->key, node->key))
                    node->base.parent->children[BITREE_NODE_LEFT] = node->base.children[BITREE_NODE_RIGHT];
                else
                    node->base.parent->children[BITREE_NODE_RIGHT] = node->base.children[BITREE_NODE_RIGHT];
            }
            else if(node->base.children[BITREE_NODE_RIGHT] == NULL) {
                if(int_compare(((BsTreeNode *)node->base.parent)->key, node->key))
                    node->base.parent->children[BITREE_NODE_LEFT] = node->base.children[BITREE_NODE_LEFT];
                else
                    node->base.parent->children[BITREE_NODE_RIGHT] = node->base.children[BITREE_NODE_LEFT];
            }
            free(node);
        }
        return 1;
    }
    return 0;
}

现实中的删除算法

如果删除的次数不多，则通常使用的策略是懒惰删除（lazy deletion）：当一个元素要被删除时，它仍留在树中，只做了个被删除的记号。这种做法特别是在有重复关键字时很常用，因为此时记录出现频率数的域可以减1。如果树中的实际节点数和“被删除”的节点数相同，那么树的深度预计只上升一个小的常数（为什么？）。因此，存在一个与懒惰删除相关的非常小的时间损耗。再有，如果被删除的关键字是重新插入的，那么分配一个新单元的开销就避免了。

二叉查找树的问题

二叉排序树的缺点是树的结构事先无法预料，随意性很大，它只与结点的值和插入的次序有关，有时会得到一颗很不平衡的二叉树。

当二叉树与理想的平衡树相差越远，树的高度越高时，其运算的时间就越长。最坏的情况下，二叉树退化成单链表，其时间复杂度由 \(O(log_2n)\) 变为\(O(n)\)。

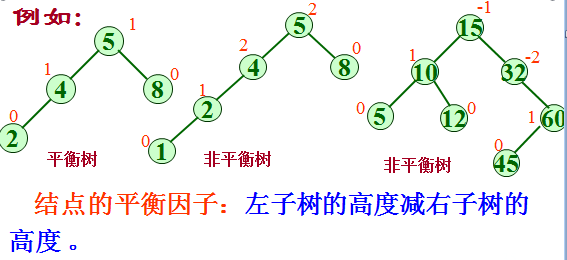
二叉平衡树的定义

二叉平衡树是一种特殊的二叉搜索树，它能有效地控制树的高度，避免产生普通二叉树的“退化”树形。

二叉平衡树（AVL树）

一棵二叉平衡树或者是空树，或者是具有下列性质的二叉排序树：它的左子树和右子树都是二叉平衡树，且左子树和右子树的高度之差的绝对值不超过1。

这是一张图片

如何构造二叉平衡树

构造平衡的二叉排序树的方法是：

根据初始序列，从空树开始插入新结点，在插入过程中，在保持二叉排序树特性的前提下，采用平衡旋转技术，对最小不平衡子树进行调整，使其平衡。

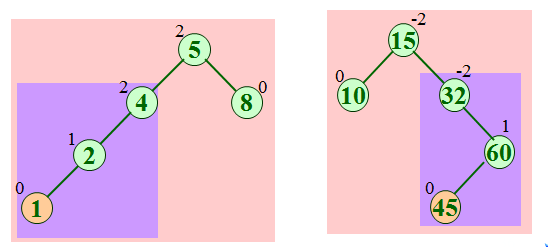
这是一张图片

如何旋转

第一种情况：插入发生在“外边”的情况（即左-左或右-右的情况），该情况通过对树的一次单旋转（single rotation）完成调整。

第二种情况：插入发生在“内部”的情况（即左-右或右-左的情况），该情况通过更复杂的双旋转（double rotation）来处理。

右单旋转

右单旋转

如果在左子树根结点的左子树上插入结点,引起不平衡，则需要进行右单旋转。以结点B为旋转轴，将结点A顺时针旋转。

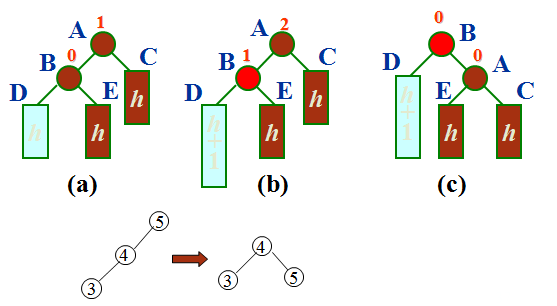
这是一张图片

左单旋转

左单旋转

如果在右子树根结点的右子树上插入结点,引起不平衡，则需要进行左单旋转，以结点C为旋转轴，让结点A逆时针旋转。

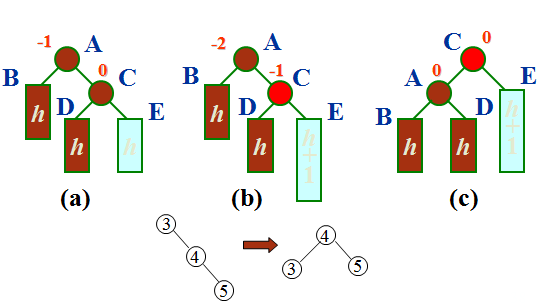
这是一张图片

先左后右双旋转

先左后右双旋转

如果在左子树根结点的右子树上插入结点，引起不平衡，则需要进行先左后右双旋转。

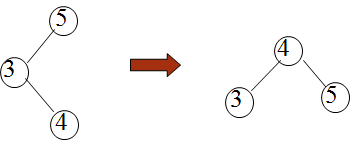
这是一张图片

先右后左双旋转

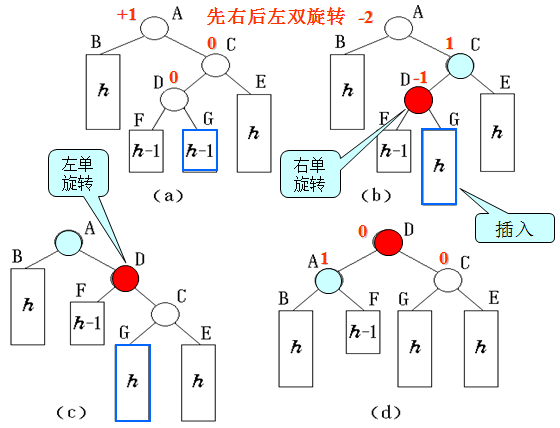
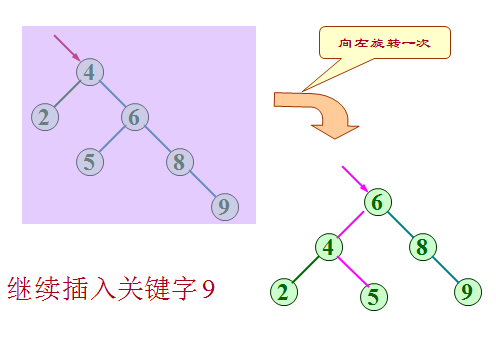
这是一张图片

二叉平衡树插入的例子

例如:依次插入的关键字为5, 4, 2, 8, 6, 9

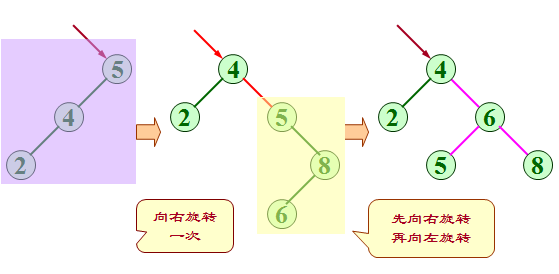
这是一张图片

二叉平衡树插入的例子续

这是一张图片

二叉平衡树的删除

1.首先不考虑平衡问题，按二叉排序树的删除原理对二叉平衡树进行删除。

2.然后再考虑平衡问题，沿被删除结点通向根的路径反向追踪检查路径上各个结点平衡因子的变化。

分三种情况考虑：

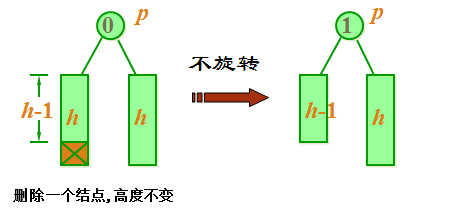
二叉平衡树的删除操作情况一

case 1: 当前结点 p 的平衡因子为0。如果它的左子树或右子树被缩短，则只需要修改它的平衡因子为 1 或-1。不需要旋转。

这是一张图片

二叉平衡树的删除操作情况二

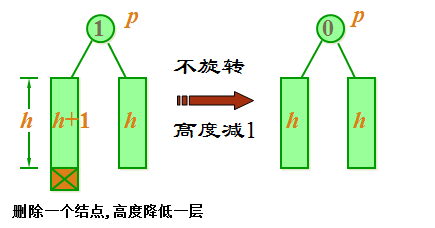
case 2: 结点 p 的平衡因子不为0，且较高的子树被缩短，则 p 的平衡因子改为0。不需要旋转。

这是一张图片

二叉平衡树的删除操作情况三

case 3: 结点 p 的平衡因子不为0，且较矮的子树又被缩短，则在结点 p 发生不平衡。需要进行平衡化旋转来恢复平衡。

令结点 p 的较高的子树的根为 q, 根据 q 的平衡因子，有如下 3 种平衡化操作：

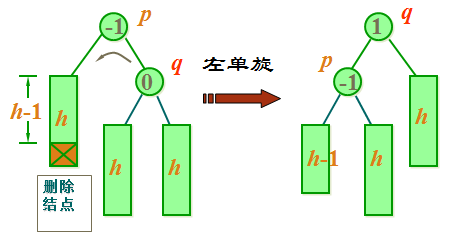
二叉平衡树的删除操作情况三分析一

case 3a: 如果 q (较高的子树) 的平衡因子为 0，执行一个单旋转来恢复结点 p 的平衡。

这是一张图片

二叉平衡树的删除操作情况三分析二

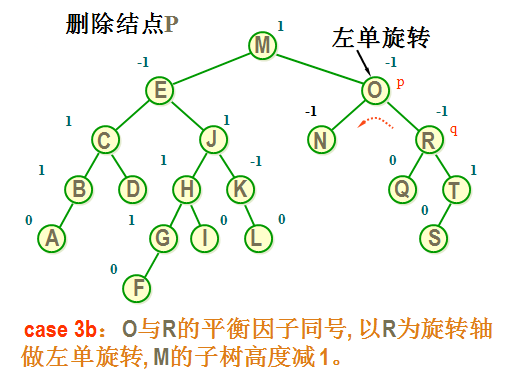
case 3b: 如果 q 的平衡因子与 p 的平衡因子相同，则执行一个单旋转来恢复平衡, 结点 p 和 q 的平衡因子均改为0。

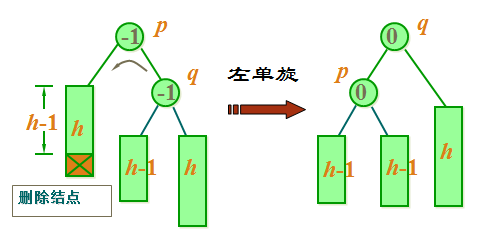
这是一张图片

二叉平衡树的删除操作情况三分析三

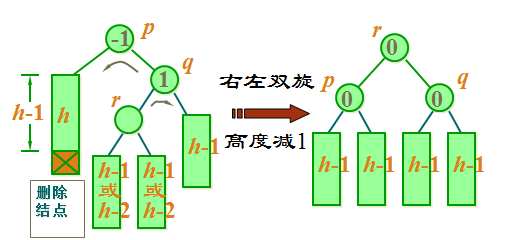
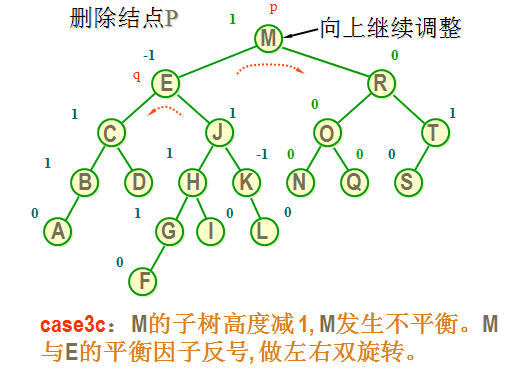
case 3c: 如果 p 与 q 的平衡因子相反, 则执行一个双旋转来恢复平衡, 先围绕 q 转再围绕 p 转。新根结点的平衡因子置为0，其它结点的平衡因子相应处理。

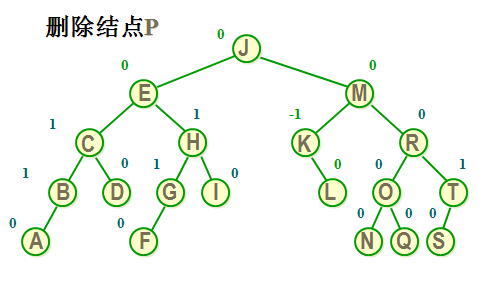
这是一张图片

二叉平衡树的删除实例

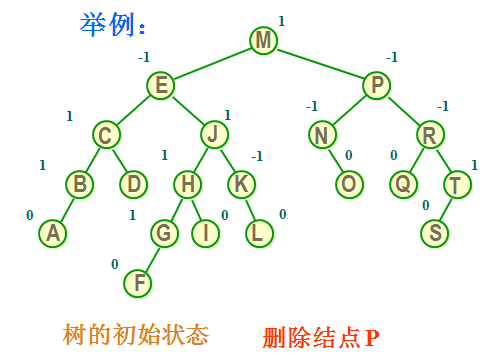
这是一张图片

二叉平衡树的删除实例续一

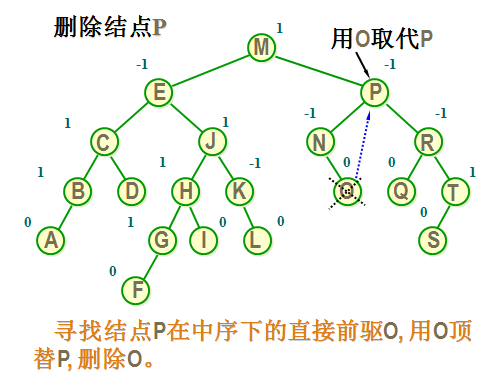
这是一张图片

二叉平衡树的删除实例续二

这是一张图片

二叉平衡树的删除实例续三

这是一张图片

二叉平衡树的删除实例续四

这是一张图片

红黑树的概念

AVL树常用的另一变种是红黑树（red black tree）。对红黑树的操作在最坏情形下需要\(O(\log N)\)时间，而在这一节中我们将介绍一种插入操作的非递归实现，它相对对于AVL树，更容易完成。

红黑树是一种二叉查找树，每一个节点都被着色为黑色或红色，且具有下列着色性质：

根节点是黑色的；
如果一个节点是红色的，那么它的子节点必须是黑色的；
从一个节点到一个\(NULL\)指针的每一条路径必须包含相同数目的黑色节点。

红黑树的效率

着色法则的一个推论是：红黑树的高度最多为\(2\log(N+1)\)。因此查找操作是一种对数操作。

红黑树较为复杂的操作在于将一个新项插入到树中。通常我们把新项作为树叶放到树中。如果把这项涂成黑色，那么就违反了性质3，因为这将会建立一条更长的黑节点的路径。因此，这一项必须涂成红色：

如果它的父节点是黑色的，则插入完成；
如果它的父节点已经是红色的，那么得到连续红色节点就会违反性质2。

在这种情况下，我们必须需要借助红黑树颜色的改变以及树的旋转操作，确保该树在不导致性质3被违反的情况下满足性质2。

B-树的概念

虽然迄今为止我们所看到的查找树都是二叉树，但是还有一种常用的查找树不是二叉树。这种树叫做B-树（B-tree）。

阶为\(M\)的B-树具有下列结构特性：

（1）树的根或者是一片树叶，或者其儿子数在2和\(M\)之间；

（2）除根外，所有非树叶节点的儿子数在\(\lceil M/2\rceil\)和\(M\)之间。

（3）所有的树叶都在相同的深度上。

B-树的性质

B-树中所有的数据都存储在树叶上。在每一个内部节点上皆含有指向该节点各儿子的指针\(P_1\)，\(P_2\)，…，\(P_M\)和分别代表在子树\(P_2\)，\(P_2\)，…，\(P_M\)中发现的最小关键字的值\(k_1\)，\(k_2\)，…，\(k_{M-1}\)。当然，可能有些指针是\(NULL\)，而其对应的\(k_i\)则是未定义的。对于每一个节点，其子树\(P_1\)中所有关键字都小于子树\(P_2\)的关键字。此外，我们还要求在非根树叶中关键字的个数也在\(\lceil M/2\rceil\)和M之间。

B-树有多种定义，这些定义在一些细节上不同于上面定义的结构，另一种常用的结构允许实际数据存储在树叶上，也可以存储在内部节点上，正如二叉查找树一样。

B-树的应用

B-树实际用于数据库系统时，树被存储在物理磁盘上而非主存中。

一般说来，对磁盘的访问要比任何主存操作慢几个数量级。如果我们使用\(M\)阶B-树，那么访问磁盘的次数是\(O(\log_M N)\)。虽然每次磁盘访问花费\(O(\log M)\)来确定分支的方向，但是执行该操作的时间一般要比读存储器的区块（block）所花费的时间少得多，因此可以被忽略不计（当M的值选择合理）。即使在每个节点更新需要花费\(O(M)\)的操作时间，这个值一般不大。此时\(M\)的值就应为一个内部节点能够装入一个磁盘区块的最大值，一般说来在\(32\leq M \leq 256\)范围内。

选择存储在一片树叶上的元素的最大个数时，要使得树叶是满的，那么它就装满一个区块。这意味着一个记录可以在很少的磁盘访问中被找到，因为典型的B-树深度只有2或3，而根（很可能还有第一层）可以放在主存中。