本次课内容

查找也称检索，是在数据结构中找出满足某种条件的结点。它是数据结构中很常用的一种基本操作。本次课将要介绍线性表上常用的查找算法，还特别要介绍一种新的数据结构，其元素和位置存在某种对应关系，查找元素时可根据关键字一次存取便可取得元素，不仅查找便捷，又能做到插入删除方便，这就是散列表。我们将要学习到：

• 查找的概念
• 线性表上的查找
• 散列表的概念
• 常见散列函数
• 解决散列函数冲突的方法
• 利用散列表查找的算法

查找的概念

在日常生活中，人们几乎每天都要进行“查找”。如在英汉字典中查找某个英文单词的中文解释；在对数表、平方根表中查找某个数的对数、平方根；邮递员送信件要按收件人的地址确定位置等等。

计算机、计算机网络使信息查询更快捷、方便、准确。要从计算机、计算机网络中查找特定的信息，就需要在计算机中存储包含该特定信息的表。如要从计算机中查找英文单词的中文解释，就需要存储类似英汉字典这样的信息表，以及对该表进行的查找操作。本章将系统地讨论各种查找方法，并通过对它们的效率分析来比较各种查找方法的优劣。

查找图例

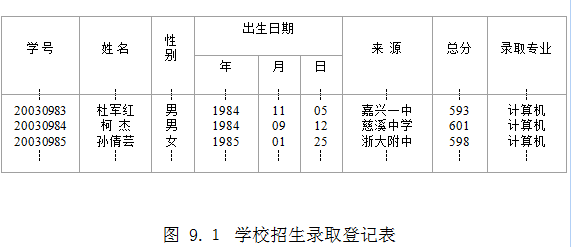
基本术语

（1）数据项 (也称项或字段)

项是具有独立含义的标识单位，是数据不可分割的最小单位。如表中“学号”、“姓名”、 “年”等。项有名和值之分，项名是一个项的标识，用变量定义，而项值是它的一个可能取值，表中“20030983”是项“学号”的一个取值。项具有一定的类型，依项的取值类型而定。

（2）组合项

由若干项构成，表中“出生日期”就是组合项，它由“年”、“月”、“日”三项组成。

（3）数据元素

数据元素又称为记录、结点、顶点等，是由若干项、组合项构成的数据单位，是在某一问题中作为整体进行考虑和处理的基本单位。数据元素有型和值之分，表中项名的集合，也即表头部分就是数据元素的类型；而一个学生对应的一行数据就是一个数据元素的值，表中全体学生即为数据元素的集合。

基本术语续一

（4）关键字

关键字（或关键码）是数据元素中某个项或组合项的值，用它可以标识一个数据元素。能唯一确定一个数据元素的关键字，称为主关键字；而不能唯一确定一个数据元素的关键字，称为次关键字。表中“学号”即可看成主关键字，“姓名”则应视为次关键字，因可能有同名同姓的学生。

（5）查找表

查找表是由具有同一类型（属性）的数据元素组成的集合。分为静态查找表和动态查找表两类。

静态查找表：仅对查找表进行查找操作，而不能改变的表；

动态查找表：对查找表除进行查找操作外，可能还要进行向表中插入数据元素，或删除表中数据元素的表。

基本术语续二

（6）查找

查找就是按给定的某个值kx，在查找表中确定关键字为给定值kx的数据元素。

关键字是主关键字时：由于主关键字唯一，所以查找结果也是唯一的，一旦找到，查找成功，结束查找过程，并给出找到的数据元素的信息，或指示该数据元素的位置。要是整个表检测完毕还没有找到，则查找失败，此时，查找结果应给出一个“空”记录或“空”指针。

关键字是次关键字时：需要查遍表中所有数据元素，或在可以肯定查找失败时，才能结束查找过程。

（7）平均查找长度

分析查找算法的效率，通常用平均查找长度ASL来衡量。平均查找长度ASL (Average Search Length)是指为确定数据元素在表中的位置所进行的关键字比较次数的期望值。

平均查找长度

对含有n个记录的表， \(ASL=\sum_{i=1}^{n}p_ic_i\)

其中：\(p_i\)为查找表中第i个元素的概率， \(\sum_{i=1}^{n}p_i=1\)

\(c_i\)为找到表中第i个元素所需比较次数

若不特别声明，均认为每个结点的查找概率相等，即

\[p_1=p_2=…=p_n=1/n\]

线性表的查找

顺序查找（Sequential Search）的查找过程为：从表中最后一个记录开始，逐个进行记录的关键字和给定值的比较，若某个记录的关键字和给定值比较相等，则查找成功，找到所查记录；反之，若直至第一个记录，其关键字和给定值比较都不等，则表明表中没有查到记录，则查找不成功。

算法描述：

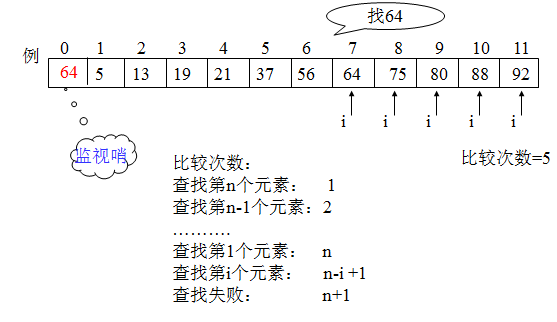
顺序查找算法

顺序查找算法:

int search_seq(StaticSearchTable st, KeyType key) {
    //在顺序表st中顺序查找其关键字等于key的数据元素。若找到，返回该元素在表中的位置，查找不成功，返回0 
    st.elem[0].key = key;   //0号单元作为监视哨 
    for(i = st.length; st.elem[i].key != key; i--); //从后往前找 
    return i;   //找不到时，i为0 
}

在该算法中，查找之前先对\(ST.elem[0]\)的关键字赋值\(key\)，目的在于免去查找过程中每一步都要检测整个表是否查找完毕。在此，\(ST.elem[0]\)起到了监视哨的作用。这仅是一个程序设计技巧上的改进，然而实践证明，这个改进能使顺序查找在\(ST.length\geq 1000\)时，进行一次查找所需的平均时间几乎减少一半。当然，监视哨也可设在高下标处。

顺序查找方法的ASL

对含有n个记录的表， \(ASL=\sum_{i=1}^{n}p_ic_i\)

认为每个结点的查找概率相等，即 p1=p2=…=pn=1/n

则 \[ ASL=\sum_{i=1}^{n}p_ic_i=1/n\sum_{i=1}^{n}(n-i+1)=(n+1)/2 \]

顺序查找的特点

顺序查找和我们后面将要讨论到的其他查找算法相比，其缺点是平均查找长度较大，特别是当\(n\)很大时，查找效率较低。

然而，它也有很大的优点：算法简单且适用面广。它对表的结构无任何要求，无论记录是否按关键字有序均可应用。

顺序查找的改进

有时，表中各个记录的查找概率并不相等。

例如：将全校学生的病历档案建立一张表存放在计算机中，则体弱多病同学的病历记录查找概率必定高于健康同学的病历记录。由于式中的\(ASL\)在\(P_{n}\geq P_{n-1}\geq \cdots \geq P_{2} \geq P_{1}\)时达到极小值。

因此，对记录的查找概率不等的查找表若能预先得知每个记录的查找概率，则应先对记录的查找概率进行品牌排序，使表中记录按查找概率由小至大重新排序，以便提高查找效率。

现实中顺序查找的改进措施

在一般情况下，记录的查找概率预先无法测定。为了提高查找效率，我们可以在每个记录中附设一个访问频度域，并使顺序表中的记录始终保持按访问频度非递减有序的次序列，使得查找概率大的记录在查找过程中不断后移，以便在以后的逐次查找中减少比较次数。或者在每次查找之后都将刚查到的记录直接移至表尾。

对查找效率的进一步思考

前面顺序查找平均查找长度的讨论是在\(\sum_{i=1}^{n} P_{i}=1\)的前提下进行的，换句话说，我们认为每次查找都是“成功”的。在实际应用的大多数情况下，查找成功的可能性比不成功的可能性大得多，特别是在表中记录数\(n\)很大时，查找不成功的概率可以忽略不计。当查找不成功的情形不能忽视时，查找算法的平均查找长度应是查找成功时的平均查找长度与查找不成功时的平均查找长度之和。

对于顺序查找，不论给定值\(key\)为何值，查找不成功时和给定值进行比较的关键字个数均为\(n+1\)。假设查找成功与不成功的可能性相同，对每个记录的查找概率也相等，则\(P_{i}=\frac {1}{2n}\)，此时顺序查找的平均长度为

有序表的查找

折半查找

查找过程：每次将待查记录所在区间缩小一半

适用条件：采用顺序存储结构的有序表

算法实现

设表长为n，low、high和mid分别指向待查元素所在区间的上界、下界和中点,kx为给定值

初始时，令low=1,high=n,mid=(low+high)/2

让k与mid指向的记录比较

若kx==tbl.elem[mid].key，查找成功

若kxtbl.elem[mid].key，则low=mid+1

重复上述操作，直至low>high时，查找失败

折半查找算法

有序表的折半查找算法:

int search_bin(StaticSearchTable st, KeyType key) {
    //在有序表中折半查找其关键字等于key的数据元素，设关键字按升序排列 
    //若找到，则返回该元素在表中的位置，否则返回0
    int low = 1, high = st.length, mid; //设置区间初值
    while(low <= high) {
        mid = (low + high)/2;
        if(st.elem[mid].key == key)
            return mid; //找到待查元素
        else if(st.elem[mid].key > key)
            high = mid - 1; //继续在前半区间进行查找 
        else
            low = mid + 1;  //继续在后半区间进行查找 
    } 
    return 0    //表中不存在待查元素 
}

折半查找图示

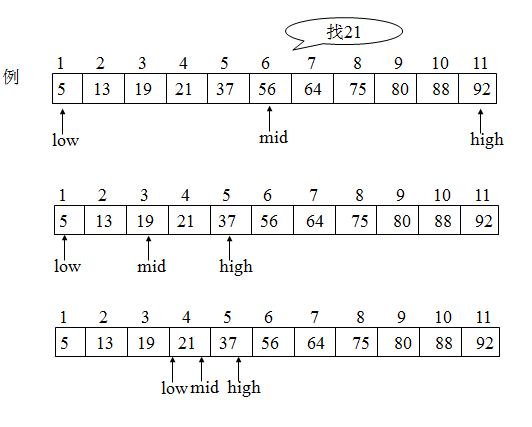
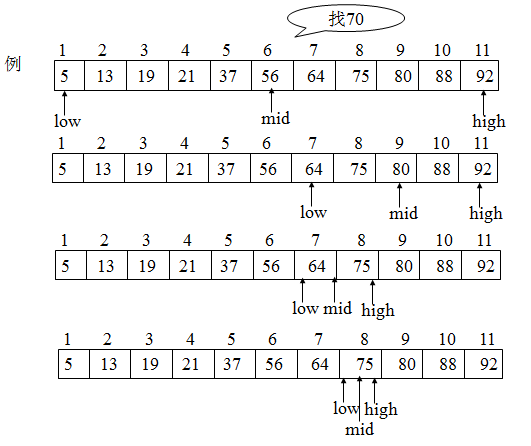
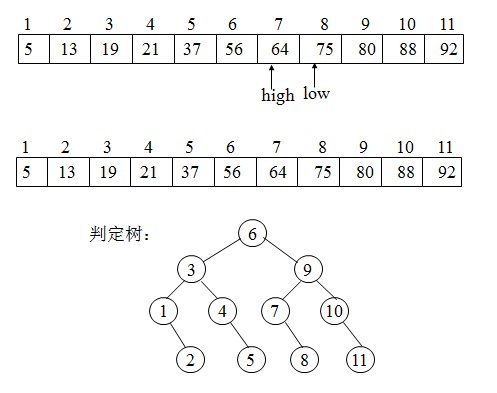
折半查找的性能分析

判定树：描述查找过程的二叉树叫判定树

有n个结点的判定树的深度为\(log_2n+1\)

折半查找法在查找过程中进行的比较次数最多不超过其判定树的深度

折半查找的ASL

设表长 \(n=2^{k}-1,h=log_2(n+1)\) ,即判定树是深度为h的满二叉树

设表中每个记录的查找概率相等，即p1=p2=…=pn=1/n

则： \[ASL=\sum_{i=1}^{n}p_ic_i=1/n\sum_{i=1}^{n}c_i\] \[ASL=1/n\sum_{i=1}^{n}j*2^{j-1}\] \[ASL=\frac{n+1}{n}log_2(n+1)-1\approx log_2(n+1)-1\]

斐波那契查找

斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。

斐波那契查找时根据斐波那契数列的特点对表进行分割的。假设开始时表中记录某个数比某个斐波那契数小1，即\(n=F_{n}-1\)，然后将给定值\(key\)和\(ST.elem[F_{u-1}].key\)进行比较，若相等，则查找成功；若\(key<ST.elem[F_{u-1}].key\)，则继续在自\(ST.elem[1]\)至\(ST.elem[F_{u-1}-1]\)的子表中查找，否则继续在\(ST.elem[F_{u-1}+1]\)至\(ST.elem[F_{u}-1]\)的子表中进行查找，后一子表的长度为\(F_{u-1}-1\)。斐波那契查找的平均性能比折半查找好，但最坏的情况下的性能（虽然仍是\(O(\log n)\)）却比折半查找差。它还有一个优点就是分割时，只需进行加、减运算。

插值查找

插值查找不同于前面讨论的几种查找算法，前面介绍的查找算法是基于严格比较的，即假定我们对线性表中元素的分布一无所知（或称没有启发式信息）。然而实际中，很多查找问题所涉及的表满足某些统计的特点。插值查找在实际使用时，一般要满足两个假设条件

（1）每一次对数据的访问与通常的指令相比，费用都是相当昂贵的。例如，待查找的表一定是在磁盘而非内存中，因而每一次比较都要进行磁盘访问。

（2）数据不仅是已被排好序的，而且呈现均匀分布特征。

插值查找是根据给定值\(key\)来确定进行比较的关键字\(ST.elem[i].key\)的查找方法。令\(i=\frac{key-ST.elem[1].key}{ST.elem[h].key-ST.elem[1].key}(h-l+1)\),其中\(ST.elem[l]\)和\(ST.elem[h]\)分别为有序表中具有最小关键字和最大关键字的记录。显然，这种插值查找只适用于关键字均匀分布的表，在这种情况系，对表长较大的顺序表，其平均性能比折半查找好。

分块查找

查找过程：将表分成几块，块内无序，块间有序；先确定待查记录所在块，再在块内查找

适用条件：分块有序表

分块查找又称索引顺序表查找，这是顺序查找的一种改进方法。在此查找法中，除表本身以外，尚需建立一个“索引表”。

分块查找的要点

用数组存放待查记录,每个数据元素至少含有关键字域

对每个子表（或称块）建立一个索引项，其中包括两项内容：关键字项（其值为该子表内的最大关键字）和指针项（指示该子表的第一个记录在表中位置）。

建立索引表，每个索引表结点含有最大关键字域和指向本块第一个结点的指针

索引表按关键字有序，则表或者有序或者分块有序。所谓“分块有序”指的是第二个子表中所有记录的关键字均大于第一个子表中的最大关键字，第三个子表中的所有关键字均大于第二个子表中的最大关键字，……，依次类推。

分块查找的实现

分块查找过程需要分两步进行。

• 先确定待查记录所在块（子表）
• 然后在块中顺序查找。

假设给定值\(key=38\)，则先将\(key\)依次和索引表中各最大关键字进行比较，因为\(22<key<48\)，则关键字为38的记录若存在，必定在第二个子表中，由于同一索引项中的指针指示第二个子表中的第一个记录是表中第7个记录，则自第7个记录起进行顺序查找，直到\(ST.elem[10].key=key\)为止。

分块查找图示

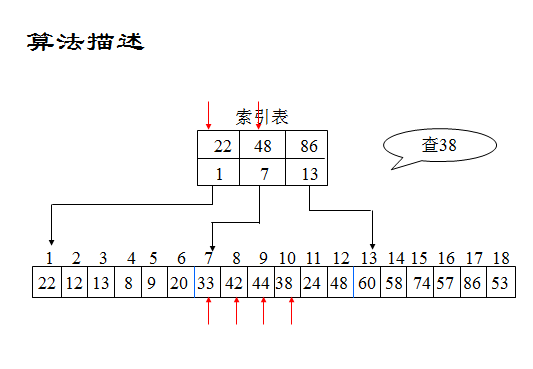
分块查找的分析

由于由索引项组成的索引表按关键字有序，则确定块的查找可用顺序查找，亦可用折半查找，而块中记录是任意排序的，则在块中只能是顺序查找。

由此，分块查找的算法即为这两种查找算法的简单合成。

分块查找的平均查找长度为

\[ASL_{bs}=L_{b}+L_{w}\]

其中：\(L_{b}\)为查找索引表确定所在块的平均查找长度，\(L_{w}\)为块中查找元素的平均查找长度。

上述查找方法的比较

散列表的查找

以上讨论的查找方法，由于数据元素的存储位置与关键字之间不存在确定的关系，因此，查找时，需要进行一系列对关键字的查找比较，即“查找算法”是建立在比较的基础上的，查找效率由比较一次缩小的查找范围决定。理想的情况是依据关键字直接得到其对应的数据元素位置，即要求关键字与数据元素间存在一一对应关系，通过这个关系，能很快地由关键字得到对应的数据元素位置。

散列（Hashing）是一种重要的存储方法，也是一种常见的查找方法。它的基本思想是：

以元素的关键字key为自变量，通过一个确定的函数关系f，计算出对应的函数值f(key)，把这个值解释为元素的存储地址，并按此存放；查找时，由同一个函数对给定值kx计算地址，将kx与地址单元中元素关键字进行比较，确定查找是否成功。因此，散列法（哈希法）又称为关键字－地址转换法。散列方法中使用的转换函数称为散列函数(哈希函数)，按这个思想构造的表称为散列表(哈希表)。

散列定义

哈希函数——在记录的关键字与记录的存储地址之间建立的一种对应关系叫哈希函数

哈希函数是一种映象，是从关键字空间到存储地址空间的一种映象

哈希函数可写成：addr(ai)=H(ki)

\(a_i\)是表中的一个元素

\(addr(a_i)\)是\(a_i\)的存储地址

\(k_i\)是\(a_i\)的关键字

哈希表——应用哈希函数，由记录的关键字确定记录在表中的地址，并将记录放入此地址，这样构成的表叫~

哈希查找——又叫散列查找，利用哈希函数进行查找的过程叫~

哈希函数示例

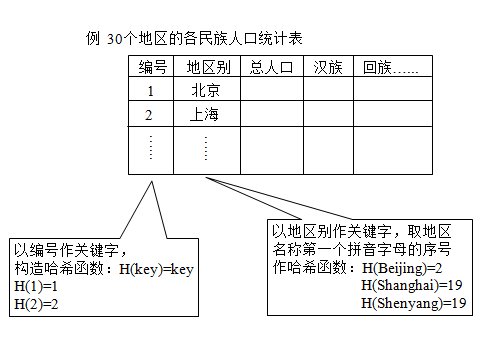
冲突现象

从例子可见：

哈希函数只是一种映象，所以哈希函数的设定很灵活，只要使任何关键字的哈希函数值都落在表长允许的范围之内即可

冲突：\(key1\neq key2\) ，但H(key1)=H(key2)的现象叫冲突

同义词：具有相同函数值的两个关键字，叫该哈希函数的同义词

哈希函数通常是一种压缩映象，所以冲突不可避免，只能尽量减少；同时，冲突发生后，应该有处理冲突的方法

构造散列函数的原则

构造一个散列函数的方法有很多，但是究竟什么是“好”的散列函数？一个理想的散列函数\(h\)应当满足下列条件：（1）能快速计算；（2）具有均匀性。

假定散列表长度为\(M\)，那么散列表函数\(h\)将关键字值转换成\([0,M-1]\)中的整数，即\(0\leq h(key) <M\)。一个均匀的散列函数应当是：如果\(key\)是从关键字值集合中随机选取的一个值，则\(h(key)\)以同等的概率取区间\([0,M-1]\)中的每一个值。

常见哈希函数——直接定址法

构造：取关键字或关键字的某个线性函数作哈希地址，即

\[H(key)=key 或 H(key)=a·key+b\]

特点:

这类函数是一一对应函数，不会发生冲突。

要求地址集合与关键字集合大小相同，因此，对于较大的关键字集合不适用。

例子：关键字集合为{100，300，500，700，800，900}，选取散列函数为H(key)=key/100，则存放如下：

常见哈希函数——数字分析法

构造：对关键字进行分析，取关键字的若干位或其组合作哈希地址

适用范围：适于关键字位数比哈希地址位数大，且可能出现的关键字事先知道的情况

常见哈希函数——平方取中法

构造：取关键字平方后中间几位作哈希地址

适用范围：适于不知道全部关键字情况

通常，要预先估计关键字的数字分布并不容易，要找数字均匀分布的位数则更难。例如下列一组关键字(0100, 0110, 1010, 1001, 0111)就无法使用数字选择法得到较均匀的散列函数。此时可采用平方取中法，即先通过求关键字的平方值扩大差别，然后再取中间的几位或其组合作为散列地址。

例如，上述一组关键字的平方结果是： \[(0010000,0012100,1020100,1002001,0012321)\] 若表长为1000，则可取中间三位作为散列地址集。

常见哈希函数——折叠法

构造：将关键字分割成位数相同的几部分，然后取这几部分的叠加和（舍去进位）做哈希地址。种类有：

移位叠加：将分割后的几部分低位对齐相加

间界叠加：从一端沿分割界来回折送，然后对齐相加

适于关键字位数很多，且每一位上数字分布大致均匀情况

例如关键字 key=58242324169，哈希地址位数为3

常见哈希函数——除留余数法

构造：取关键字被某个不大于哈希表表长m的数p除后所得余数作哈希地址，即

\[H(key)=key MOD p，p\leqslant m\]

一般选P为小于或等于散列表长度m的某个最大素数比较好。

例如： \[m=8,16,32,64,128,256,512,1024\] \[P=7,13,31,61,127,251,503,1019\]

特点：

• 简单、常用，可与上述几种方法结合使用
• p的选取很重要，p选的不好，容易产生同义词

解决冲突的方法

上面的讨论表面，一个散列表中冲突时难免的。因此寻求较好的解决冲突的方法是一个重要的问题。解决冲突也称为“溢出”处理技术。有两种常用解决冲突的方法，拉链法和开放地址法。拉链法也成开散列法，而开放地址法又称为闭散列法。请注意此处名称问题，以免引起混淆。

链地址法

方法：将所有关键字为同义词的记录存储在一个单链表中，并用一维数组存放头指针

拉链法解决冲突的方法是：把具有相同散列地址的关键字值放在同一个单链表中，这个单链表称为同义词链表。若选定的散列函数的值域为0～m-1，则可将散列表定义为一个有m个头指针组成的指针数组HTP[m]，凡是散列地址为i的结点，均插入到以HTP[i] 为头指针的单链表中。

链地址法例子

例：已知一组关键字(26, 36, 41, 38, 44, 15, 68, 12, 06, 51, 25)，散列函数为 H(key) MOD 13，用拉链法解决冲突构造这组关键字的散列表。

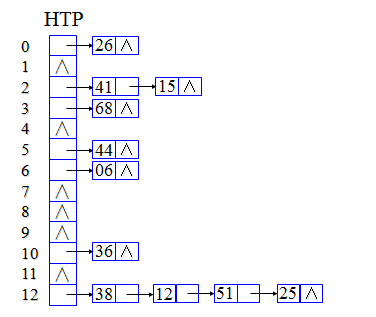
链地址法的要点

同义词单链表可以是无序的，也可按升序（或降序）排序。如图显示了这种方法。该例子采用除法散列函数，除数为11，同义词按升序排列。

在拉链的散列表中搜索一个元素是容易的：首先要计算待查元素的散列地址，然后搜索该地址的单链表。

在插入时：同样先计算新元素的散列地址，然后按在有序表中插入一个新元素的方法，在同义词链表中插入操作。

开放定址法

方法：当冲突发生时，形成一个探查序列；沿此序列逐个地址探查，直到找到一个空位置（开放的地址），将发生冲突的记录放到该地址中，即Hi=(H(key)+di)MOD m，i=1,2,……k(k≤m-1)

其中：

H(key)——哈希函数

m——哈希表表长

di——探查序列

不同的解决冲突的策略，可产生不同的需要被检查的未知的序列，称为探查序列。探查表中空闲位置的探查序列形如

\[h(key),(h(key)+p(1))mod M,\cdots,(h(key)+p(i))mod M,\cdots\]

根据生成探查序列的规则不同，可以有线性探查法、伪随机探查法、二次探查法和双散列法等开放地址法。

开放定址法——线性探查法

线性探查法是一种最简单的开放地址法。它使用下列循环探查序列，即

\[h(key),h(key)+1,\cdots,M-1,0,\cdots,h(key)-1\]

从基位置\(h(key)\)开始，探查该位置是否被占用，即是否为空位置，如果被占用，则继续检查位置\(h(key)+1\)，若该位置也已占用，再检查由探查序列规定的下一个位置……

可将线性探查法的探查序列记为

\[h_i=(h(key)+1) mod M i=0,1,2,\cdots,M-1\]

线性探查法图示

采用除数为11的除法散列函数。为了在图(a)中插入关键字值为38的元素，先计算基位置\(h(38)=38\) \(mod\)\(11=5\)。从图中可见，位置5已占用，线性探查法需检查下一个位置。位置8当前闲置，所以可将38插入位置8处。如果需继续插入关键字值24,24可直接插在关键字值的基地址2处。

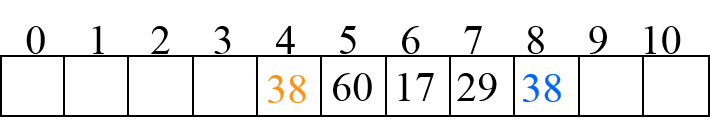
• H(38)=38 MOD 11=5 冲突
• H1=(5+1) MOD 11=6 冲突
• H2=(5+2) MOD 11=7 冲突
• H3=(5+3) MOD 11=8 不冲突

线性探查法对应的查找

对线性探查散列表的搜索同样从基位置\(h(key)\)开始，按照上面描述的线性循环探查序列查找该元素。设\(key\)是待查关键字值，若存在关键字值为\(key\)的元素，则搜索成功，否则，或者遇到一个空位置，或者回到\(h(key)\)（说明此时表已满），则搜索失败。

线性探查法的删除

在散列表中删除一个元素由两点需要考虑：一是删除过程不能简单地将一个元素清除，这会隔离探查序列后的元素，从而影响以后的元素搜查过程；二是一个元素被删除后，希望该元素的位置应当能够重新使用。

从图中删除60，不能简单地将位置5设置为空，这样会使得以后无法找到38。

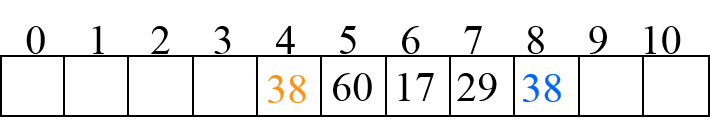
通过对表中每个元素增设一个标志位（设为empty），上述两点可望解决。空散列表的所有元素的标志位被初始化为true。当向表中存入一个新元素时，存入位置处的标志位置成false。删除元素时并不改变元素的标志位，只是将该元素的关键字值设置成一个从不使用的特殊值，不放设置为空值（设为NeverUsed）。

开放定址法——二次探查法

二次探测再散列：di=1²,-1²,2²,-2²,3²,……, k²,-k² (k≤(m-1)/2)

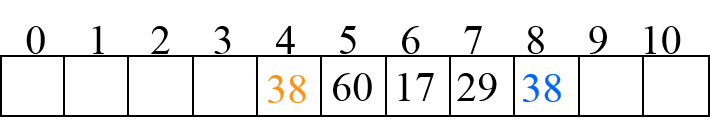
• H(38)=38 MOD 11=5 冲突
• H1=(5+1²) MOD 11=6 冲突
• H2=(5-1²) MOD 11=4 不冲突

开放定址法——双散列法

双散列法使用两个散列函数，第一个散列函数计算探查序列的起始值，第二个散列函数计算下一个位置的探查步长。

设表长为\(M\)，双散列法的探查序列\(H_0,H_1,H_2,\cdots\)为

\[h_1(key),(h_1(key)+h_2(key))mod M,(h_1(key)+2*h_2(key))mod M,\cdots\]

双散列法的探查序列也可以写成

\[H_i=(h_1(key)+i*h_2(key))mod M,i-0,1,\cdots,M-1\]

设\(M\)是散列表的长度，则对任意\(key\),\(h_2(key)\)应是小于\(M\)，且与\(M\)互质的整数。这样的探查序列能够保证最多经过\(M\)次探查便可遍历表中的所有地址。

例如，

若\(M\)是素数，可取\(h_2(key)=key\) \(mod\) \((M-2)+1\)。

\(h_1(key)=key\) \(mod\) \(11\)，\(h_2(key)=key\) \(mod\) \(9 +1\)

装填因子

散列表的装填因子定义为：

\[\alpha=\frac{\text{填入表中的元素个数}}{\text{散列表的长度}}\]

\(\alpha\)是散列表装满程度的标志因子。由于表长是定值，\(\alpha\)与“填入表中的元素个数”成正比，所以，\(\alpha\)越大，填入表中的元素较多，产生冲突的可能就越大；\(\alpha\)越小，填入表中的元素较少，产生冲突的可能性就越小。

再散列

对于使用平方探查的开放定址散列法，如果表的元素填的太满， 那么操作的运行时间将开始消耗过长，且插入操作可能失败，这可能发生在有太多的移动和插入混合的场合。

此时，一种解决方法是建立另外一个大约两倍大的表（而且使用一个相关的新散列函数），扫描整个原始散列表，计算每个（未删除的）元素的新散列值并将其插入到新表中。

例如，设将元素13,15,24和6插入到大小为7的开放定址散列表中，散列函数是\(h(key)=key\) \(mod\) \(7\)。设使用线性探查法解决冲突问题。

如果将23插入表中，那么插入后的表将有超过70%的单元是满的。因为表过满，所以我们建立一个新的表。该表大小之所以为17，是因为17是原表大小两倍后的第一个素数。新的散列函数为\(h(key)=key\) \(mod\) \(17\)。扫描原来的表，并将元素6,15,23,24以及13插入到新表中。

再散列分析

上面的操作叫做再散列（rehashing）。显然这是一种昂贵的操作：其运行时间为\(O(n)\)，因为有\(n\)个元素要再散列，而表的大小约为\(2n\)。

不过，由于不是经常发生，因此实际效果根本没有那么差。特别是，在最后的再散列之前必然已经存在\(n/2\)次插入。

添加到每个插入上的基本是一个常数开销。如果这种数据结构是程序的一部分，那么其效果是不显著的。另一方面，如果再散列作为交互系统的一部分运行，那么其插入引起再散列的用户将会感受到运行速度减慢。

再散列的时机

• 一种做法是只要表满到一半就进行再散列。
• 另一种方法是只有当插入失效时才再散列。
• 第三种方法即途中（middle-of-the-road）策略：当表到达某一个装填因子时进行再散列。

由于随着装填因子的增加，会导致表的性能下降，因此，以合适的截止手段实现第三种策略，可能是最好的实现方法。

再散列使得程序员不再需要担心表的大小，因为在复杂的程序中，散列表的大小不能够做的任意大，因此再散列的实现非常重要。

散列表的查找过程

散列表的查找过程基本上和造表过程相同。一些关键字可通过散列函数转换的地址直接找到，另一些关键字在散列函数得到的地址上产生了冲突，需要按处理冲突的方法进行查找。在介绍的三种处理冲突的方法中，产生冲突后的查找仍然是给定值与关键字进行比较的过程。所以，对散列表查找效率的度量，依然用平均查找长度来衡量。

散列表分析示例

关键字(19,14,23,1,68,20,84,27,55,11,10,79)

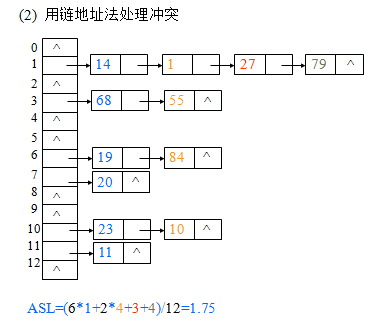
影响散列表查找性能

查找过程中，关键字的比较次数，取决于产生冲突多少的因素，也就是影响查找效率的因素。影响产生冲突多少有以下三个因素：

1）散列函数是否均匀；

2）处理冲突的方法；

3）散列表的装填因子。

分析这三个因素，尽管散列函数的“好坏”直接影响冲突产生的频度，但一般情况下，我们总认为所选的散列函数是“均匀的”，因此，可不考虑散列函数对查找平均长度的影响。

哈希查找性能分析

散列方法存储速度快，也较为节省空间，静态查找、动态查找均适用，但由于存取是随机的，因此不便于顺序查找。

在有\(n\)个元素的散列表中搜索、插入和删除一个元素的时间，最坏情况下均为\(O(n)\)。但散列表的平均性能还是相当好的，

现在使用均匀的散列函数计算地址，又设\(A_{s}(n)\)是成功搜索一个随机选择的关键字值的平均比较次数，那么采用上述不同的方法调节冲突时散列表的平均搜索长度为：

散列表的实现

我们使用拉链法为例来实现散列结构。几个重要的结构体：

struct _HashTable {
    HashTableEntry **table;
    unsigned int table_size;
    HashTableHashFunc hash_func;
    HashTableEqualFunc equal_func;
    HashTableKeyFreeFunc key_free_func;
    HashTableValueFreeFunc value_free_func;
    unsigned int entries;
    unsigned int prime_index;
};

struct _HashTableEntry {
    HashTableKey key;
    HashTableValue value;
    HashTableEntry *next;
};

和普通的链式结构一样，散列表中的每个结点都有指向下一个结点的指针\(next\)。在我们的散列表实现中，关键词\(key\)和结点中存储的数据\(value\)是没有联系的，所以在结点中\(ksy\)和\(value\)为两个独立变量。

结构体解释

• \(table\)指针是访问散列表的入口。
• \(table\_size\)是散列表的大小，指的是该散列中链表的数量，在这种散列的实现中，\(table\_size\)具体值是由\(prime\_index\)和一个素数集合决定，不直接修改。
• \(hash\_func\)是散列表的哈希函数，输入一个关键词返回地址。
• \(equal\_func\)是散列表种用于判断两个关键词是否相同的函数。
• \(key\_free\_func\)和\(value\_free\_func\)分别是用于释放结点关键词和数据的函数，可以使用\(hash\_table\_register\_free\_functions\)函数记录到散列表结构中，也可以缺省。
• 整数\(entries\)用于记录散列表中已被使用的结点数量。
• \(prime\_index\)指示一个下标，在一个素数集合中，该下标所指示的素数即为散列表的大小。

散列表初始化

建立一个新的散列表需要传入函数\(hash\_func\)和\(equal\_func\)的指针。

HashTable *hash_table_new(HashTableHashFunc hash_func,
                          HashTableEqualFunc equal_func){
    HashTable *hash_table;

    /* 分配一个内存空间 */
    hash_table = (HashTable *) malloc(sizeof(HashTable));
    if (hash_table == NULL)
        return NULL;
    hash_table->hash_func = hash_func;
    hash_table->equal_func = equal_func;
    hash_table->key_free_func = NULL;
    hash_table->value_free_func = NULL;
    hash_table->entries = 0;
    hash_table->prime_index = 0;

    /* 给每个结点分配内存空间，结点数量为table_size */
    if (!hash_table_allocate_table(hash_table)) {
        free(hash_table);
        return NULL;
    }
    return hash_table;
}

散列表查找操作

首先通过哈希函数\(hash\_func\)和\(key\)计算出需要遍历的链表下标\(index\)，然后遍历该链表，直到找到关键词为\(key\)的结点，并返回该节点的数据，否则返回\(HASH\_TABLE\_NULL\)。

HashTableValue hash_table_lookup(HashTable *hash_table, HashTableKey key){
    HashTableEntry *rover;
    unsigned int index;

    /* 根据关键词找到对应链表头结点的下标 */ 
    index = hash_table->hash_func(key) % hash_table->table_size;

    /* 遍历下标为index的链表直到找到关键词为key的结点 */
    rover = hash_table->table[index];
    while (rover != NULL) {
        if (hash_table->equal_func(key, rover->key) != 0)

            /* 找到目标结点，返回数据. */
            return rover->value;
        rover = rover->next;
    }

    /* 未找到结点 */
    return HASH_TABLE_NULL;
}   

散列表插入操作

我们先对已使用的结点数在散列表中所占的比例进行判断，如果已使用超过1/3的空间，那么就对散列表进行扩大。

int hash_table_insert(HashTable *hash_table, HashTableKey key,
                      HashTableValue value){
    HashTableEntry *rover;
    HashTableEntry *newentry;
    unsigned int index;
    
    /* 如果表中的结点过多，冲突的可能性增大，散列表的查找效率下降，此时扩大表的大小 */
    /* 当已使用的结点数量超过散列表大小的1/3 */ 
    if ((hash_table->entries * 3) / hash_table->table_size > 0)
        if (!hash_table_enlarge(hash_table))

            /* 分配内存失败 */
            return 0;

    /* 根据关键词找到对应链表头结点的下标 */ 
    index = hash_table->hash_func(key) % hash_table->table_size;

    /* 遍历整个链表来查找是否有相同关键词的结点，有则覆写，否则添加 */
    rover = hash_table->table[index];
    while (rover != NULL) {
        if (hash_table->equal_func(rover->key, key) != 0) {

            /* 若找到相同关键词，用新数据覆写结点 */
            /* 如果有释放数值和关键词内存的函数，那么释放旧内存，没有则跳过 */
            if (hash_table->value_free_func != NULL)
                hash_table->value_free_func(rover->value);
            if (hash_table->key_free_func != NULL)
                hash_table->key_free_func(rover->key);
            rover->key = key;
            rover->value = value;
            
            /* 覆写完成 */
            return 1;
        }
        rover = rover->next;
    }

    /* 没有关键词为key的结点，那么在新建一个并加入链表头部 */
    newentry = (HashTableEntry *) malloc(sizeof(HashTableEntry));
    if (newentry == NULL)
        return 0;
    newentry->key = key;
    newentry->value = value;

    /* 插入序号为index的链表头部 */ 
    newentry->next = hash_table->table[index];
    hash_table->table[index] = newentry;

    /* 链表中结点的数量增加1 */
    hash_table->entries++;

    /* 添加完成 */
    return 1;
}

再散列操作

static int hash_table_enlarge(HashTable *hash_table) {
    HashTableEntry **old_table;
    unsigned int old_table_size;
    unsigned int old_prime_index;
    HashTableEntry *rover;
    HashTableEntry *next;
    unsigned int index;
    unsigned int i;

    /* 复制一份旧表结构并存储 */
    old_table = hash_table->table;
    old_table_size = hash_table->table_size;
    old_prime_index = hash_table->prime_index;

    /* 给一个新的表分配更大的内存 */
    ++hash_table->prime_index;

    if (!hash_table_allocate_table(hash_table)) {

        /* 为新表分配内存失败 */
        hash_table->table = old_table;
        hash_table->table_size = old_table_size;
        hash_table->prime_index = old_prime_index;
        return 0;
    }

    /* 把所有结点链接进新生成的表中 */
    for (i=0; i < old_table_size; ++i) {
        rover = old_table[i];

        while (rover != NULL) {
            next = rover->next;

            /* 在新的表中找到原关键词对应的链表序号 */
            index = hash_table->hash_func(rover->key)
                  % hash_table->table_size;

            /* 把结点接入序号是index的链表 */
            rover->next = hash_table->table[index];
            hash_table->table[index] = rover;

            /* 链表中的下一个 */
            rover = next;
        }
    }

    /* 释放旧表的占用的内存 */
    free(old_table);
    return 1;
}

散列表删除操作

在函数中传入散列表指针和关键词\(key\)，功能是删除散列表中关键词为\(key\)的结点。

int hash_table_remove(HashTable *hash_table, HashTableKey key){
    HashTableEntry **rover;
    HashTableEntry *entry;
    unsigned int index;
    int result;

    /* 根据关键词找到对应链表头结点的下标 */ 
    index = hash_table->hash_func(key) % hash_table->table_size;
    result = 0;
    rover = &hash_table->table[index];
    while (*rover != NULL) {
        if (hash_table->equal_func(key, (*rover)->key) != 0) {

            /* 找到将要被移除的结点 */
            entry = *rover;

            /* 从链表中脱离 */
            *rover = entry->next;

            /* 销毁结点结构 */
            hash_table_free_entry(hash_table, entry);
            hash_table->entries--;
            result = 1;
            break;
        }

        /* 探查链表的下一个结点 */
        rover = &((*rover)->next);
    }
    return result;
}

树表

从前面的讨论可知:

当线性表作为表的组织形式时，可以有顺序查找、折半查找及其变种、分块查找三种方法法，其中以折半查找效率最高。但由于折半查找要求表中结点按关键字有序，且不能用链表作存储结构，因此，当表的插入或删除操作频繁时，为维护表的有序性，势必要移动表中很多结点，这种由移动结点引起的额外时间开销，就会抵消折半查找的优点。

散列表的优点是将读取的效率做到极致，其不足是散列表是不排序的，hash表中元素之间的位置关系是随机的，没有任何规律可言。现实中我们希望手机通信录中的联系人是按姓氏排序的，如果使用散列表，就需要额外的内存空间进行排序。

对于需要动态操作或需要排序的场合，可采用几种特殊的二叉树（如二叉排序树、平衡二叉树）或树（如B-树、B+树）作为表的一种组织方式，在此将它们统称为树表。

实验内容

实现一个散列表，并完成：

• 清晰的注释
• 具有再散列功能
• 能够处理冲突
• 具有性能相关的测试