数据结构与算法
数组和矩阵
2017年春
本次课内容
矩阵是很多科学与工程计算问题中研究的数学对象。在此,我们感兴趣的不是矩阵本身,而是如何存储矩阵的元,以及如何使矩阵的各种运算能有效地进行。本章是线性表在科学计算中的应用。我们将要学习到:
- 矩阵和数组的关系
- 特殊矩阵的压缩存储方法
- 稀疏矩阵的十字链表表示方法
- 矩阵运算的算法实现
二维数组
数组是我们很熟悉的一种数据结构,它可以看作线性表的推广。数组作为一种数据结构其特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型,比如:一维数组可以看作一个线性表,二维数组可以看作“数据元素是一维数组”的一维数组,三维数组可以看作“数据元素是二维数组”的一维数组,依此类推。下图是一个m行n列的二维数组。

数组特点
特点:
- 数组结构固定
- 数据元素同构
数组运算:
- 取值操作:给定一组下标,读其对应的数据元素。
- 赋值操作:给定一组下标,存储或修改与其相对应的数据元素。
以行序为主序
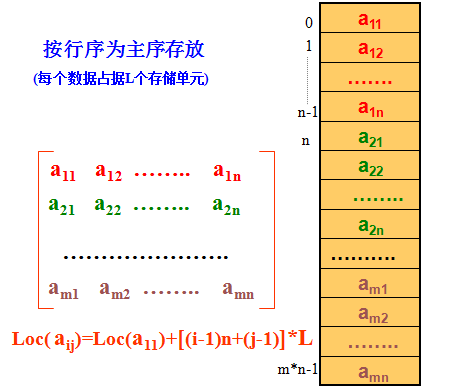
以列序为主序
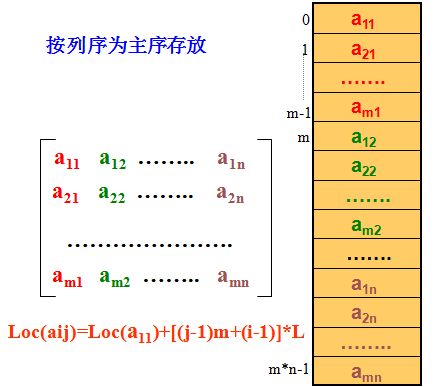
矩阵的二维数组实现
创建一个矩阵
typedef double ** densematrix;
/* 创建一个矩阵 */
densematrix dm_create(int mu, int nu) {
int i;
densematrix A = (double **)malloc(sizeof(double *)*(mu+1));
for(i = 1; i <= mu; i++)
A[i] = (double *)malloc(sizeof(double)*(nu+1));
return A;
}矩阵相加
/* 把矩阵B加到矩阵A上 */
void dm_plus(densematrix A, densematrix B, int mu, int nu) {
int i, j;
for(i = 1; i <= mu; i++)
for(j = 1; j <= nu; j++)
A[i][j] = A[i][j]+B[i][j]; /* 矩阵相加规则是两个矩阵同一下标所对应的元相加 */
}稠密矩阵乘法
/* 矩阵乘法 */
densematrix dm_mult(densematrix A, densematrix B, int amu, int bnu, int anu) {
int i, j, k;
/* 矩阵乘法只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义,矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。 */
densematrix C = dm_create(amu, bnu);
for(i = 1; i <= amu; i++)
for(j = 1; j <= bnu; j++) {
C[i][j] = 0;
for(k = 1; k <= anu; k++)
C[i][j] += A[i][k]*B[k][j]; /* 矩阵乘法运算规则 */
}
return C;
}稀疏矩阵
若数值为0的元素数目远远多于非0元素的数目时,则称该矩阵为稀疏矩阵(sparse matrix);与之相反,若非0元素数目占大多数时,则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。稠密度小于等于0.05时,则称该矩阵为稀疏矩阵。
在数值分析中经常出现一些阶数很高的稀疏矩阵。有时为了节省存储空间,可以对这类矩阵进行压缩存储。所谓压缩存储是指:为多个值相同的元只分配一个存储空间;对零元不分配空间。
假若值相同的元素或者零元素在矩阵中的分布有一定规律(如上三角矩阵、下三角矩阵、对角矩阵),则称该矩阵为特殊矩阵。下面分别讨论它们的压缩存储。
对称矩阵
对称矩阵
若\(n\)阶矩阵\(A\)中的元满足下述性质 \[a_{ij}=a_{ji} \text{$1\leq i$, $j\leq n$}\] 则成为\(n\)阶对称矩阵。
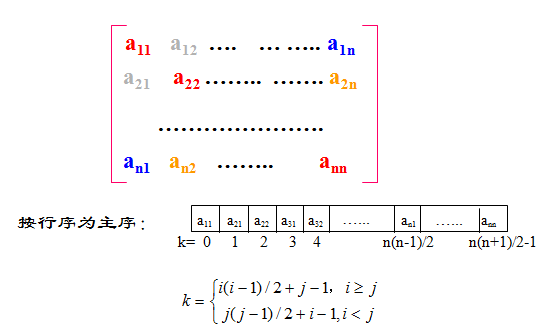
三角矩阵
形如下图所示的矩阵称为三角矩阵

带状矩阵
对于一个\(n\)阶矩阵\(A\),如果存在最小正整数\(m\),满足当\(\mid i-j \mid \geq m\)时,\(a_{ij}=0\),则\(A\)为带状矩阵,称\(w=2m-1\)为矩阵\(A\)的带宽。
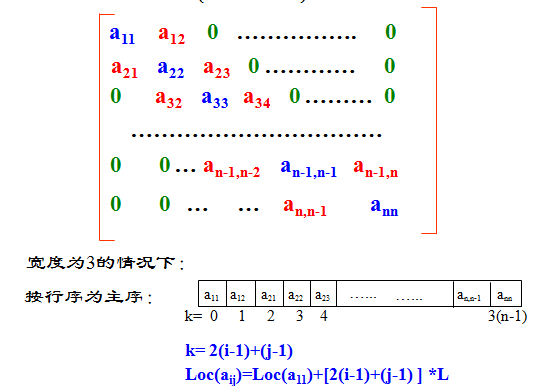
稀疏矩阵的压缩存储
定义:假设在\(m\times n\)的矩阵中,有\(t\)个元素不为零。令\(\delta=\cfrac{t}{m\times n}\),称\(\delta\)为矩阵的稀疏因子,通常认为\(\delta\leq0.05\)时为稀疏矩阵。
在很多科学管理以及工程运算中,常会遇到阶数很高的大型稀疏矩阵,如果按常规的分配方法,顺序分配在计算机内,那将是相当浪费内存的。为此提出另外一种存储方法,仅仅存放非零元素。但对于这类矩阵,通常零元素分布没有规律,为了能找到相应的元素,仅存储非零元素的值是不够的,还要记下它所在的行和列的位置\((i,j)\)。反之,一个三元组\((i,j,a_{ij})\)唯一确定了矩阵A的一个非零元。由此,稀疏矩阵可由表示非零元的三元组及其行列数唯一确定。
压缩存储原则:只存矩阵的行列维数和每个非零元的行列下标及其值

M由{(1,2,12), (1,3,9), (3,1,-3), (3,6,14), (4,3,24),(5,2,18), (6,1,15), (6,4,-7) } 和矩阵维数(6,7)唯一确定
三元组顺序表存储
将三元组按行优先顺序,同一行中列号从小到大的规律排列成一个线性表,称为三元组表。以顺序存储结构来表示三元组表,则可得稀疏矩阵的一种压缩存储方式——三元组顺序表。
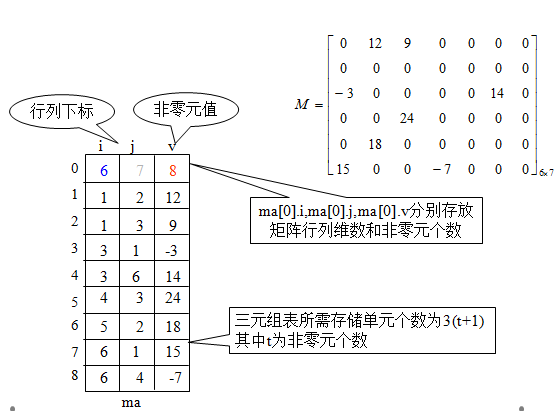
三元组表
三元组的类型说明如下:
#define SMax 1024 /* 一个足够大的数 */
typedef double MatrixValue;
typedef struct {
int row, col; /* 非零元素的行、列 */
MatrixValue val; /* 非零元素值 */
} SPNode; /* 三元组类型 */
typedef struct {
int mu, nu, tu; /* 矩阵的行数、列数及非零元素的个数 */
SPNode data[SMax+1]; /* 三元组表 */
} SPMatrix; /* 三元组表的存储类型 */求转置矩阵
问题描述:已知一个稀疏矩阵的三元组表,求该矩阵转置矩阵的三元组表
稀疏存储带来的问题
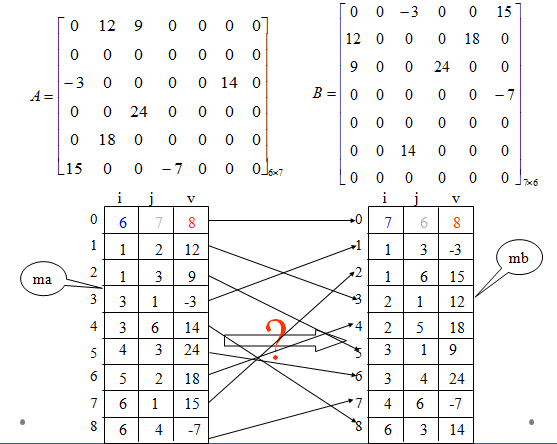
解决思路
只要做到
- 将矩阵行、列维数互换
- 将每个三元组中的 \(i\) 和 \(j\) 相互调换
- 重排三元组次序,使mb中元素以B的行(A的列)为主序
方法:按M的列序转置
稀疏矩阵转置算法
按照\(b.data\)中三元组的次序依次在\(a.data\)中找到相应的三元组进行转置。换句话说,按照矩阵\(M\)的列序来进行转置。为了找到\(M\)的每一列中所有的非零元素,需要对其三元组表\(a.data\)从第一行起整个扫描一遍,由于\(a.data\)是以\(M\)的行序为主序来存放每个非零元的,由此得到的恰是\(b.data\)应有的顺序。
SPMatrix * sm_transpose1(SPMatrix * a) {
SPMatrix * b;
int p, q, col;
b = (SPMatrix *)malloc(sizeof(SPMatrix)); /* 申请存储空间 */
b->mu = a->nu;
b->nu = a->mu;
b->tu = a->tu;
if(b->tu > 0) { /* 有非零元素则转换 */
q = 0;
for(col = 1; col <= a->nu; col++) /* 按M的列序转换 */
for(p = 1; p <= a->tu; p++) /* 扫描整个三元组表 */
if(a->data[p].col == col) {
b->data[q].row = a->data[p].col;
b->data[q].col = a->data[p].row;
b->data[q].val = a->data[p].val;
q++;
}
}
return b;
}稀疏矩阵转置图示
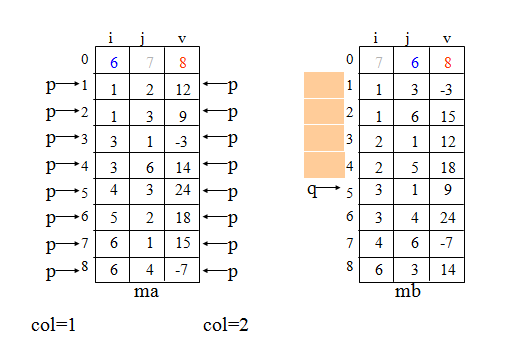
转置操作复杂度分析
分析上述算法,主要的工作是在\(p\)和\(col\)的两重循环中完成的,故算法的时间复杂度为\(O(nu\cdot tu)\),即和\(M\)的列数及非零元的个数的乘积成正比。
一般矩阵转置算法:
for(col=0;col<n;col++)
for(row=0;row<m;row++)
n[col][row]=m[row][col];时间复杂度:
\(T(n)=O(m*n)\)
虽然节省了存储空间,但时间复杂度提高了,因此算法仅适用于\(tu<<mu\times nu\)的情况。
稀疏矩阵转置的改进算法
目标 :按照\(a.data\)中三元组的次序进行转置,并将转置后的三元组置入\(b\)中恰当的位置。
解决思路:如果能预先确定矩阵\(M\)中每一列(即\(T\)中每一行)的第一个非零元在\(b.data\)中应有的位置,那么在对\(a.data\)中的三元组依次作转置时,便可直接放到\(b.data\)中恰当的位置上去。
具体做法:为了确定这些位置,在转置前,应先求得\(M\)的每一列中非零元的个数,进而求得每一列的第一个非零元在\(b.data\)中应有的位置。需要附设\(num\)和\(cpot\)两个向量。\(num[col]\)表示矩阵\(M\)中第\(col\)列中非零元的个数,\(cpot[col]\)指示\(M\)中第\(col\)列的第一个非零元在\(b.data\)中的恰当位置。
\[ \begin{cases} cpot[1]=1;\\ cpot[col]=cpot[col-1]+num[col-1] & \text{$2\leq col\leq a.nu$} \end {cases} \]
快速转置算法
这种转置方法称为快速转置,其算法实现为:
#define CMax 512 /* 一个足够大的列数 */
SPMatrix * sm_transpose2(SPMatrix * a) {
SPMatrix* b;
int i, j, k;
int num[CMax+1], cpot[CMax+1];
b = (SPMatrix *)malloc(sizeof(SPMatrix));
b->mu = a->nu;
b->nu = a->mu;
b->tu = a->tu;
if(b->tu > 0) { /* 有非零元素则转换 */
for(i = 1; i <= a->nu; i++)
num[i] = 0;
for(i = 1; i <= a->tu; i++) { /* 求矩阵M中每一列非零元素的个数 */
j = a->data[i].col;
num[j]++;
}
cpot[1] = 1;
for(i = 2; i <= a->nu; i++)
cpot[i] = cpot[i-1]+num[i-1];
for(i = 1; i <= a->tu; i++) { /* 扫描三元组表 */
j = a->data[i].col; /* 当前三元组的列号 */
k = cpot[j]; /* 当前三元组在T.data中的位置 */
b->data[k].row = a->data[p].col;
b->data[k].col = a->data[p].row;
b->data[k].val = a->data[p].val;
cpot[j]++;
}
}
return b;
} 快速转置算法分析
快速算法仅比前一个算法多用了两个辅助向量。从时间上看,算法中有4个并列的单循环,循环次数分别为\(nu\)和\(tu\),因而总的时间复杂度为\(O(nu+tu)\)。在\(M\)的非零元个数\(tu\)和\(mu\times nu\)等数量级时,其时间复杂度为\(O(mu\times nu)\),和经典算法的时间复杂度相同。
三元组表特点:
三元组顺序表又称有序的双下标法,它的特点是,非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。然而,若需按行号存取某一行的非零元,则需从头开始进行查找。
行逻辑连接的顺序存储
为了便于随机存取任意一行的非零元,则需知道每一行的第一个非零元在三元组表中的位置。为此,可将上节快速转置矩阵的算法中创建的,指示“行”信息的辅助数组\(cpot\)固定在稀疏矩阵的存储结构中。称这种“带行链接信息”的三元组表为行逻辑链接的顺序表,其类型描述如下:
typedef struct {
SPNode data[SMax]; /* 三元组表 */
int rpos[RMax+1]; /* 各行第一个非零元的位置表 */
int mu,nu,tu; /* 矩阵的行数、列数和非零元个数 */
} RLSMatrix;稀疏矩阵乘法
\[C=A\times B\]
稀疏矩阵相乘的基本操作是:
对于\(A\)中每个元素\(A.data[p](p=1,2,\cdots ,A.tu)\),找到\(B\)中所有满足条件\(A.data[p].j=B.data[q].i\)的元素\(B.data[q]\),求得\(A.data[p].v\)和\(B.data[q].v\)的乘积,而从式得知,乘积矩阵\(C\)中每个元素的值是个累计和,这个乘积\(A.data[p].val\times B.data[q].val\)只是\(C[i][j]\)中的一部分。
为便于操作,应对每个元素设一累计和的变量,其初值为零,然后扫描数组\(A\),求得相应元素的乘积并累加到适当的求累计和的变量上。
稀疏矩阵相乘算法实现要点:
两个稀疏矩阵相乘的乘积不一定是稀疏矩阵。反之,即使式中每个分量值\(A(i,k)\times B(k,j)\)不为零,其累加值\(C[i][j]\)也可能为零。因此乘积矩阵\(C\)中的元素是否为非零元,只有在求得其累加和后才能得知。由于\(C\)中元素的行号和\(A\)中元素的行号一致,又\(A\)中元素排列是以\(A\)的行序为主序的,由此可对\(C\)进行逐行处理,先求得累计求和的中间结果(\(C\)的一行),然后再压缩存储到\(C.data\)中去
C初始化;
if(C是非零矩阵) { /* 逐行求积 */
for(arow = 1; arow <= A.mu; arow++) { /* 处理M的每一行 */
ctemp[] = 0; /* 累加器清零 */
计算C中第arow行的积并存入ctemp[]中;
将ctemp[]中非零元压缩存储到C.data中;
}
}稀疏矩阵链式存储结构
当矩阵的非零元个数和位置在操作过程中变化较大时,就不宜采用顺序存储结构来表示三元组的线性表。例如,在作“将矩阵\(B\)加到矩阵\(A\)上”的操作时,由于非零元的插入或删除会引起\(A.data\)中元素的移动。为此,对这种类型的矩阵,采用链式存储结构表示三元组的线性表更为恰当。
十字链表
设行指针数组和列指针数组,分别指向每行、列第一个非零元。
结点定义
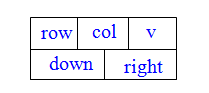
其中:row域存储非零元素的行号;col域存储非零元素的列号;v域存储本元素的值;right是行指针域,用来指向本行中下一个非零元素;down是列指针域,用来指向本列中下一个非零元素。
十字链表图示
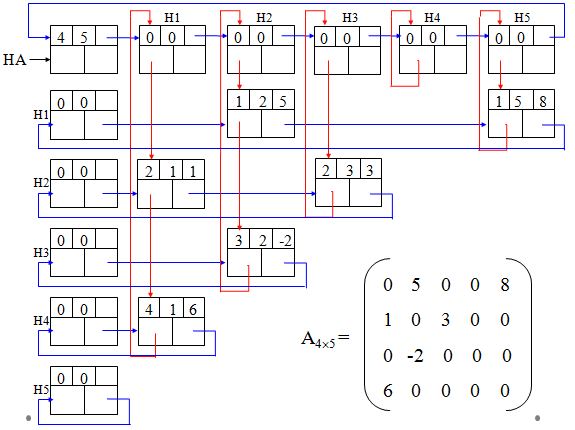
十字链表特点
稀疏矩阵中每一行的非零元素结点按其列号从小到大顺序由right域链成一个带表头结点的循环行链表,同样每一列中的非零元素按其行号从小到大顺序由down域也链成一个带表头结点的循环列链表。即每个非零元素aij既是第i行循环链表中的一个结点,又是第j列循环链表中的一个结点。
为了方便地找到每一行或每一列,将每行(列)的这些头结点们链接起来,因为头结点的值域空闲,所以用头结点的值域作为连接各头结点的链域,即第i行(列)的头结点的值域指向第i+1行(列)的头结点,… ,形成一个循环表。
空间上的改进
行链表、列链表的头结点的row域和col域置0。由于行链表头结点只用right指针域,列链表头结点只用down指针域,故这两组表头结点可以合用,也就是说对于第i行的链表和第i列的链表可以共用同一个头结点。
这个循环表又有一个头结点,这就是最后的总头结点,指针HA指向它。总头结点的row和col域存储原矩阵的行数和列数。
结构体的改进
因为非零元素结点的值域是datatype类型,而在表头结点中需要一个指针类型才能把表头结点链成一个单循环链表。为了使整个结构的结点一致,我们规定表头结点和其它结点有同样的结构,因此该域用一个联合来表示。改进后的结点结构如下图所示。
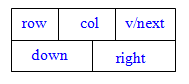
结点的结构
结点的结构定义如下:
typedef double MatrixValue;
typedef struct OLNode {
int row, col; /* 该非零元的行和列下标 */
MatrixValue val; /* 该非零元的值 */
struct OLNode *down, *right; /* 该非零元所在行表和列表的后继链域 */
} OLNode, *OLink;
typedef struct {
OLNode *rhead, *chead; /* 行表头和列表头的指针 */
int mu, nu, tu; /* 矩阵的行数、列数及非零元个数 */
} OList; /* 十字链表矩阵结构 */下面让我们看基于这种存储结构的稀疏矩阵的运算。这里将介绍两个算法,创建一个稀疏矩阵的十字链表和用十字链表表示的两个稀疏矩阵的相加。
建立稀疏矩阵
1.十字链表A
首先输入的信息是:m(A的行数),n(A的列数),t(非零项的数目),紧跟着输入的是t个形如(i,j,aij)的三元组。
算法的设计思想:
- 首先建立每行(每列)只有头结点的空链表,并建立起这些头结点拉成的循环链表;
- 然后每输入一个三元组(i,j,aij),则将其结点按其列号的大小插入到第i个行链表中去,同时也按其行号的大小将该结点插入到第j个列链表中去。
- 在算法中将利用一个辅助数组 hd[s+1],其中 \(s=max(m , n)\) , \(hd [i]\) 指向第i行(第i列)链表的头结点。这样做可以在建立链表时随机地访问任何一行(列),为建表带来方便。
建立稀疏矩阵的十字链表算法
OList olink_create(int mu, int nu, int tu) { /* 建立十字链表 */
OList olist;
OLink p, q;
int i, row, col;
MatrixValue val;
olist.rhead = (OLNode *)malloc(sizeof(OLNode)*mu);
for(i = 0; i < mu; i++)
olist.rhead[i].right = NULL;
olist.chead = (OLNode *)malloc(sizeof(OLNode)*nu);
for(i = 0; i < nu; i++)
olist.chead[i].down = NULL;
olist.tu = tu;
olist.mu = mu;
olist.nu = nu;
for(i = 1; i <= tu; i++) {
printf("请输入行号,列号,数值:");
scanf("%d,%d,%lf", &row, &col, &val);
p = olnode_setvalue(row, col, val);
q = &(olist.rhead[row-1]);
while(q->right != NULL && q->right->col < col) /* 将p插入行链中 */
q = q->right;
p->right = q->right;
q->right = p;
q = &(olist.chead[col-1]);
while(q->down != NULL && q->down->row < row) /* 再将p插入列链中 */
q = q->down;
p->down = q->down;
q->down = p;
}
return olist;
}十字链表稀疏矩阵的加法
已知两个稀疏矩阵A和B,分别采用十字链表存储,计算 \(C=A+B\) ,C也采用十字链表方式存储,并且在A的基础上形成C,即A改成了C。
由矩阵的加法规则知,只有A和B行列对应相等,二者才能相加。
C中的非零元素 \(cij\) 只可能有3种情况:
- \(aij+bij\)
- \(aij (bij=0)\)
- \(bij (aij=0)\)
因此当B加到A上时,对A十字链表的当前结点来说,对应下列四种情况:
- 改变结点的值( \(aij+bij≠0\) );
- 删除一个结点( \(aij+bij=0\) );
- aij不变( \(bij=0\) );
- 插入一个新结点( \(aij=0\) )。
整个运算从矩阵的第一行起逐行进行。对每一行都从行表的头结点出发,分别找到A和B在该行中的第一个非零元素结点后开始比较,然后按四种不同情况分别处理。
十字链表稀疏矩阵的乘法
以矩阵\(A\)的行序为主循环,以矩阵\(B\)的列序为次循环。新得到的结点在相乘得到的矩阵\(C\)中的插入方式与转置操作类似。
OL_SPMatrix olsm_mult(OL_SPMatrix A, OL_SPMatrix B) {
OL_SPMatrix M;
OLink p, q, qa, qb, pre;
int i, j;
ElementType x;
if(A.nu != B.mu) { /* 判断A矩阵列数是否等于B矩阵行数 */
printf("Error:Size mismatch");
return M;
}
M.mu = A.mu;
M.nu = B.nu;
M.rhead = (OLNode *)malloc(sizeof(OLNode)*M.mu);
for(i = 0; i < M.mu; i++)
M.rhead[i].right = NULL;
M.chead = (OLNode *)malloc(sizeof(OLNode)*M.nu);
for(i = 0; i < M.nu; i++)
M.chead[i].down = NULL;
for(i = 1; i <= M.mu; i++) {
pre = &(M.rhead[i-1]);
for(j = 1; j <= M.nu; j++) {
qa = A.rhead[i-1].right;
qb = B.chead[j-1].down;
x = 0;
while(qa != NULL && qb != NULL) {
if(qa->col < qb->row)
qa = qa->right;
else if(qa->col > qb->row)
qb = qb->down;
else { /* 有列号与行号相同的元素才相乘 */
x = x+qa->val*qb->val;
qa = qa->right;
qb = qb->down;
}
}
if(x) {
p = olnode_setvalue(i, j, x);
pre->right = p; /* 将p插入到第i行中 */
pre = p;
q = &(M.chead[j-1]);
while(q->down != NULL)
q = q->down;
q->down = p; /* 将p插入到第j列中 */
}
}
}
return M;
}实验内容
用十字链表存储结稀疏矩阵,并完成:
- 清晰的注释
- 遍历十字链表(输出矩阵到屏幕)
- 矩阵的转置、相加
- 矩阵相乘
- 用实例验证上面功能的正确性