本次课程内容

栈和队列是两类特殊的线性表，对它们进行插入和删除元素时只能在表的两端进行，因此它们是运算受限的线性表。栈和队列在算法设计中经常用到，是非常重要的数据结构。我们将要学习到：

• 顺序栈和链栈的实现
• 栈如何应用于表达式计算
• 栈和递归的关系
• 顺序队列和链式队列的实现

栈的定义

栈的定义和特点

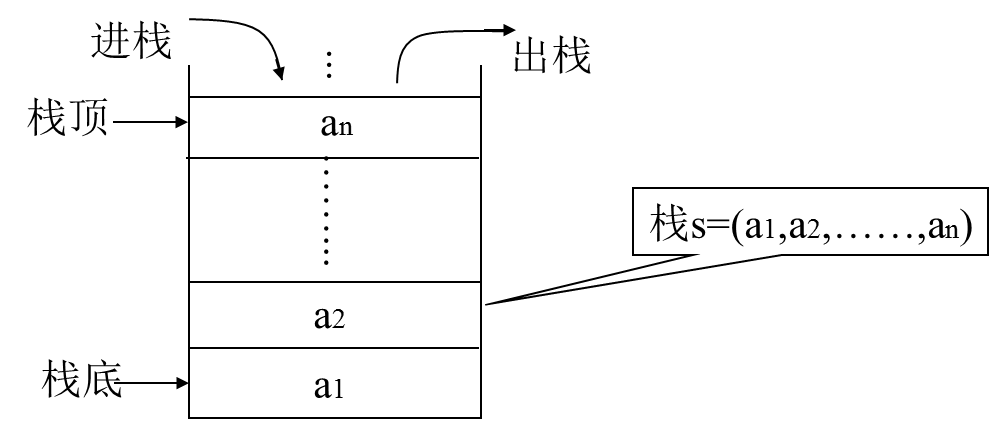
定义：限定仅在表尾进行插入或删除操作的线性表，表尾—栈顶，表头—栈底，不含元素的空表称空栈

特点：先进后出（FILO）或后进先出（LIFO）

栈ADT

栈的基本操作除了插入和删除外，还有建立和撤销栈等操作，栈的抽象数据类型定义见程序。

creat_stack：建立一个空栈。

dispose_stack：撤销一个栈。

is_empty：若栈空，则返回true；否则返回false。

is_full：若栈满，则返回true；否则返回false。

top：在x中返回栈顶元。若操作成功，则返回true；否则返回false。

push：在栈顶插入元素x(入栈)。

pop：从栈中删除栈顶元素(出栈)。

make_empty：清除堆栈中全部元素。

栈的顺序表示

顺序栈

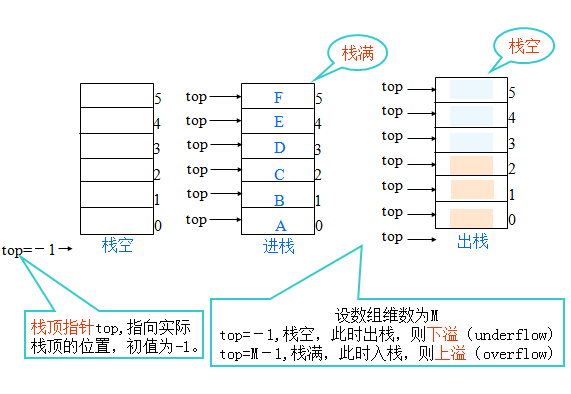
如同线性表一样，栈也有顺序和链接两种表示方式。栈的顺序表示方式也用一维数组加以描述，这样的栈称为顺序栈。

顺序栈用ArrayList实现

顺序栈的类型和变量定义如下：

顺序栈结构中包括最大栈顶指针(下标)、当前栈顶指针和指向数组的指针，可以用第三章中已经写好的抽象数据类型\(ArrayList\)来实现。其中，最大栈顶指针可用\(ArrayList\)结构中的\(\_alloced\)来表示、当前栈顶指针可以用\(length-1\)来表示，指向数组的指针用\(data\)表示。

顺序栈的头文件

顺序栈的头文件

#include "arraylist.h"

/* 建立一个新的栈 */
ArrayList *seqstack_new(unsigned int length);

/* 销毁一个栈 */
void seqstack_free(ArrayList *seqstack);

/* 在栈顶插入元素 */
int seqstack_push(ArrayList *seqstack, ArrayListValue data);

/* 从栈中删除栈顶元素 */
ArrayListValue seqstack_pop(ArrayList *seqstack);

/* 读取栈顶元素 */
ArrayListValue seqstack_peek(ArrayList *seqstack);

/* 判断栈是否为空 */
int seqstack_is_empty(ArrayList *seqstack);

顺序栈的代码

栈的基本操作除了插入和删除外，还有建立和撤销栈等操作。

ArrayList *seqstack_new(unsigned int length) {
    ArrayList *seqstack = arraylist_new(length);    //可调用ArrayList中函数实现
    return seqstack;
}

void seqstack_free(ArrayList *seqstack) {
    arraylist_free(seqstack);
}

int seqstack_is_empty(ArrayList *seqstack) {
    return seqstack == NULL;
}

顺序栈的关键代码

顺序栈的关键代码

int seqstack_push(ArrayList *seqstack, ArrayListValue data) {
    return arraylist_append(seqstack, data);    //在数组的尾部添加一个数据
}

ArrayListValue seqstack_pop(ArrayList *seqstack) {
    ArrayListValue result = seqstack->data[seqstack->length-1];
    arraylist_remove(seqstack, seqstack->length-1); //移除数组尾部的一个数据
    return result;
}

ArrayListValue seqstack_peek(ArrayList *seqstack) {
    if (seqstack_is_empty(seqstack)) 
        return NULL;
    else 
        return seqstack->data[seqstack->length-1];  //返回栈顶元素
}

顺序栈的实际实现

实际上把seqstack_前缀改成arraylist_，把下面方法作为ArrayList的方法，在使用时把ArrayList当做栈用即可。

/* 在栈顶插入元素 */
int arraylist_push(ArrayList *seqstack, ArrayListValue data);

/* 从栈中删除栈顶元素 */
ArrayListValue arraylist_pop(ArrayList *seqstack);

/* 读取栈顶元素 */
ArrayListValue arraylist_peek(ArrayList *seqstack);

/* 判断栈是否为空 */
int arraylist_is_empty(ArrayList *seqstack);    

链栈

用链式存储结构实现的栈称为链栈。通常链栈用单链表表示，因此其结点结构与单链表的结构相同。

定义top为栈顶指针，链栈示意图如下：

链式栈的结点结构定义和操作的实现类似于单链表，因此，可以使用前面已经写好的抽象数据类型单链表\(SList\)来实现。

链栈基本操作实现算法

链栈的实现：

SListEntry *slist_push(SListEntry **linkedStack, SListValue data) {
    return slist_prepend(linkedStack, data);    //在链表头插入数据
}

SListValue slist_pop(SListEntry **linkedStack) {
    SListValue result = slist_nth_data(*linkedStack, 0);
    if(slist_remove_entry(linkedStack, *linkedStack))   //移除链表头的数据
        return result;
    return SLIST_NULL;
}

SListValue slist_peek(SListEntry *linkedStack) {
    return slist_nth_data(linkedStack, 0);  //返回链表头的数据指针
}

栈的应用举例——表达式计算

表达式计算是程序设计语言编译中的一个最基本问题，在表达式求值过程中用到栈。作为栈的应用实例，下面介绍表达式计算。

在高级语言程序中存在着各种表达式，例如\(a/(b-c)+d*e\)。表达式由操作数、操作符和界限符组成。一个表达式中，如果操作符在两个操作数之间，则成为中缀表达式。中缀表达式是表达式的最常见的形式，在程序设计语言中普遍使用。

操作符优先级

为正确计算表达式的值，任何程序设计语言都必须明确规定各操作符的优先级，如C语言中部分操作符的优先级。

C语言规定的表达式计算顺序为：有括号时先计算括号中的表达式；高优先级先计算；同级操作符计算有两种情况，有的从左向右，也有的从右向左计算。

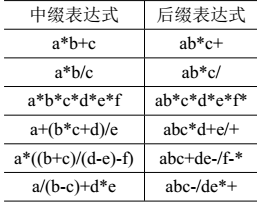
后缀表达式

尽管中缀表达式是普遍使用的书写形式，但在编译程序中常用表达式的后缀形式求值，原因是后缀表达式中无括号，计算时无需考虑操作符的优先级(事实上，后缀表达式中的操作符已经按中缀表达式计算的先后顺序排列好)，因而计算简单。把操作符放在两个操作数之间的表达式称为后缀表达式，又称为逆波兰表达式。

后缀表达式计算过程

后缀表达式的计算过程为：从左往右顺序扫描后缀表达式，遇到操作数就进栈，遇到操作符就从栈中弹出两个操作数，执行该操作符规定的运算，并将结果进栈。如此下去，直达遇到结束符"#"结束。弹出栈顶元素即为结果。注意，这里表达式中只讨论双目操作符，在计算从栈中弹出的两个操作数时，先出栈的放操作符的右边，后出栈的放左边。

后缀表达式 \(abc-/de*+\) (中缀表达式为\(a/(b-c)+d*e\))的计算过程\((a=6,b=4,c=2,d=3,e=2)\)

中缀表达式转换为后缀表达式

由于后缀表达式具有计算简便等优点，因此编译程序中常将中缀表达式转换为后缀表达式。这种转换也是栈应用的一个典型例子。

在中缀和后缀两种形式中，操作数的顺序是相同的。因此很容易得到转换过程：

1. 从左到右逐个扫描中缀表达式中各项，遇到结束符“#”转(6)，否则继续；
2. 遇到操作数直接输出；
3. 若遇到右括号“)”，则连续出栈输出，直到遇到左括号“(”为止(注意：左括号出栈但并不输出)，否则继续；
4. 若是其他操作符，则和栈顶的操作符比较优先级，若小于等于栈顶操作符的优先级，则连续出栈输出，直到大于栈顶操作符的优先级结束，操作符进栈；
5. 转(1)继续；
6. 输出栈中剩余操作符(#除外)。

中缀转后缀的要点

为了方便算法的实现，在后缀表达式的后面，加上1个后缀表达式的结束符“#”。

实现转换的关键是确定操作符的优先级，因为优先级决定了操作符是否进、出栈。操作符在栈内外的优先级应该有所不同，以体现中缀表达式同优先级操作符从左到右的计算要求。

左括号的优先级在栈外最高，但进栈后应该比除“#”外的操作符低，可使括号内的其他操作符进栈。为此，设计了栈内优先级isp(in-stack priority)和栈外优先级icp(incoming priority)。

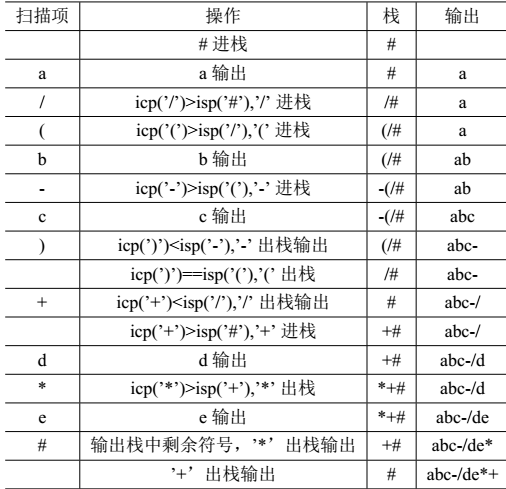
中缀转后缀的例子

\(a/(b-c)+d*e\)转换为后缀表达式\(abc-/de*+\)的过程:

利用两个栈计算表达式

除了将中缀表达式转化为后缀表达式进行计算，另一种计算表达式的方法是使用两个栈，直接对输入的表达式进行计算。

设置的两个栈分别为算子栈和算符栈，算子栈用于存放操作数，算符栈用于存放操作符。计算的过程如下：

1. 将表达式以字符串形式读入，从左到右扫描表达式字符串，遇到字符串结束符“\0”转(6)，否则继续；
2. 若遇到操作数，直接进算子栈；
3. 若遇到左括号“(”，则之后直接计算完对应的一对括号内的子表达式；
4. 若遇到右括号“)”，则计算完对应的这对括号内的子表达式，将结果压入栈中；
5. 若遇到除括号外的操作符，则和算符栈的栈顶操作符比较优先级：若小于等于栈顶操作符的优先级，则从算子栈中出栈两个操作数，算符栈的栈顶操作符出栈，出栈的操作数和操作符用于计算，先出栈的操作数计算时在后，将计算结果压入算子栈中。读到的操作符继续和栈顶操作符比较优先级，直到大于栈顶操作符的优先级，操作符进算符栈。
6. 扫描完成后，算符栈中还有剩余操作符，则依次弹出所有的操作符，每弹出一个操作符，相应的弹出两个算子进行计算，先出栈的操作数计算时在后，将计算的结果压入算子栈中。最终在算子栈栈顶的操作数即为计算结果。

计算表达式实现——主要函数

int is_valid_exp(char *);   /* 判断括弧是否匹配 */
int table(char op); /* 返回运算符的优先级数 */
double operate(char *,int);    /* 计算表达式的值 */
double calculate(double,double,char);    /* 计算两个数的运算和 */

主函数：

int main(void) {
    char exp[1000]; /* 存储输入的表达式字符串 */
    puts("请输入您要计算的表达式:");
    gets(exp);
    if(is_valid_exp(exp)) {
        puts("计算结果如下:");
        printf("%s = ", exp);
        printf("%.3f\n", operate(exp, strlen(exp)));
    }
    else
        puts("表达式输入错误，括号不匹配!");
    return 0;
}

计算表达式实现—辅助函数

int table(char op) {
    switch(op) {
        case '+':
        case '-':
            return 12;
        case '*':
        case '/': 
        case '%':   
            return 13;
        case ';':
        case '\0': 
        case ')':   
            return 1;
    }
    return -1;
}

double calculate(double val1, double val2, char op) {
    switch(op) {
        case '+':
            return(val1+val2);
        case '-':
            return(val1-val2);
        case '*':
            return(val1*val2);
        case '/':
            return(val1/val2);
    }
    return -1;
}

计算表达式实现-主要函数

/* len:表达式字符串串长度 */
/* k:当前读取的位置 */
double operate(char *exp, int len) {
    int nop = 0,a;  /* 算符个数 */
    ArrayList *ns;
    double val1, val2;
    char  *os, op, opin;
    ArrayListValue temp;
    /* 根据需要申请空间 */
    ns = seqstack_new(1000);    /* 算子栈 */
    os = (char *)malloc(len*sizeof(char));  /* 算符栈 */
    os[nop] = ';';
    while((*(exp + k)) != '\0') {
        if((*(exp + k)) == '(') {
            k++;
            temp = (double *)malloc(sizeof(double));
            *(double *)temp = operate(exp, len-k);
            a = seqstack_push(ns, temp);    /* 计算完括号的表达式，压入栈中 */
        } 
        else if((*(exp+k)) == ')') {
            k++;
            break;
        }
        else {
            if((*(exp+k)) == ' ')   /* 跳过空格 */
                k++;
            else if('0' <= (*(exp+k)) && (*(exp+k)) <= '9') {   /* 处理数字 */
                temp = (double *)malloc(sizeof(double));
                *(double *)temp = 0;
                do {
                    *(double *)temp = *(double *)temp*10 + ((double)(*(exp+k)-'0'));
                    k++;
                } while ('0' <= (*(exp+k)) && (*(exp+k)) <= '9');
                seqstack_push(ns, temp);
            }
            else {  /* 处理运算符 */
                opin = *(os+nop);   /* 栈顶的算符 */
                op = (*(exp+k));
                if (table(opin) >= table(op)) { /* 比较两个运算符的优先级 */
                    /* 从算子栈中退出两个算子 */
                    val2 = *(double *)seqstack_pop(ns);
                    val1 = *(double *)seqstack_pop(ns);
                    temp = (double *)malloc(sizeof(double));
                    *(double *)temp = calculate(val1,val2,opin);
                    seqstack_push(ns, temp);    /* 计算结果压入栈中 */
                    nop--;  /* 相当于算符栈中退栈 */
                } 
                else {
                    /* 将算符压入栈中 */
                    k++;
                    nop++;
                    *(os+nop) = op;
                }
            }           
        }
    }   
    /* 弹出算符栈中的所有算符，并计算 */
    while(nop > 0) {    
        opin = *(os+nop);
        val2 = *(double *)seqstack_pop(ns);
        val1 = *(double *)seqstack_pop(ns);
        temp = (double *)malloc(sizeof(double));
        *(double *)temp = calculate(val1, val2, opin);
        seqstack_push(ns, temp); /* 计算结果压入栈中 */
        nop--;  /* 相当于算符栈中退栈 */
    }
    temp = seqstack_pop(ns);
    seqstack_free(ns);  /* 释放空间 */
    free(os);
    return *(double *)temp;
}

递归的例子

递归：函数直接或间接的调用自身叫递归。

实现：建立递归工作栈

例: 递归的执行情况分析

void print(int  w) {
    int i;
    if ( w!=0) {
        print(w-1);
        for(i = 1; i <= w; ++i)
            printf("%3d,",w);
            printf("/n");
        }
    }
}
  

运行结果：

1，

2，2，

3，3，3，

递归调用执行情况

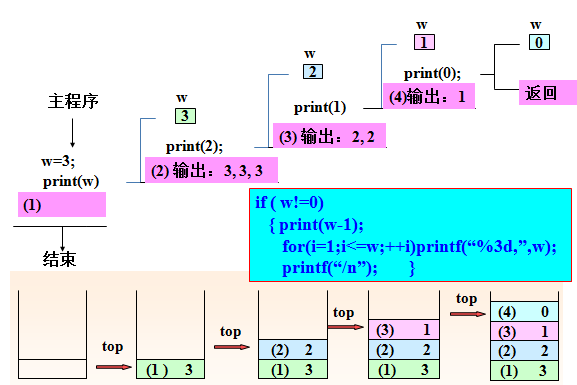
递归的概念

递归是一个数学概念，也是一种有用的程序设计方法。在程序设计中，处理重复性计算最常用的办法是组织迭代循环，此外还可以采用递归计算的办法，特别是非数值计算领域中更是如此。递归本质上也是一种循环的程序结构，它把“较复杂”的计算逐次归结为“较简单”的情形的计算，一直归结到“最简单”的情形的计算，并得到计算结果为止。许多问题采用递归方法来编写程序，使得程序非常简洁和清晰，易于分析。

关于递归，有几个重要并且容易混淆的地方。一个常见的问题是：它是否就是循环逻辑(cicular logic)？答案是：虽然我们用函数本身来定义一个函数，但是我们并没有用函数本身定义函数的一个特定实例。换句话说，通过\(f(5)\)求得\(f(5)\)才是循环的。而通过使用\(f(4)\)来求的\(f(5)\)的值并不是循环的。当然，除非\(f(4)\)的值又需要用到对\(f(5)\)的计算。

递归的优缺点

递归算法的优点是明显的：程序非常简洁和清晰，且易于分析。但它的缺点是费时间、费空间。

首先，系统实现递归需要有一个系统栈，用于在程序运行时间处理函数调用。系统栈是一块特殊的存储区。当一个函数被调用时，系统创建一个工作记录，称为栈帧(stack frame)，并将其置于栈顶。初始时只包含返回地址和指向上一个帧的指针。当该函数调用另一个函数时，调用函数的局部变量、参数将加到它的栈帧中。一旦一个函数运行结束，将从栈中删除它的栈帧，程序控制返回原调用函数继续执行下去。

操作系统是如何处理递归的

假定\(main\)函数调用函数\(a_1\)，图(a)所示为\(main\)函数系统栈，而图(b)所示为包括函数\(a_1\)的系统栈。

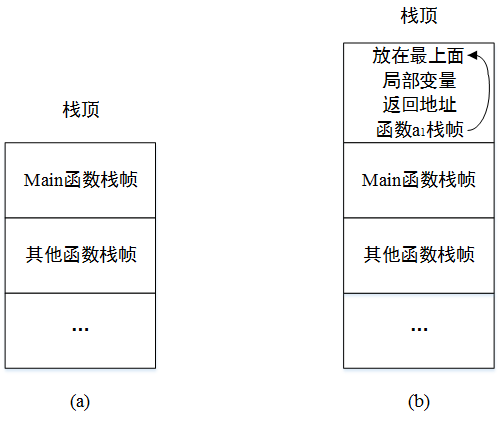
使用递归的注意点

递归的实现是费空间的，进栈出栈也是费时的，如果可能，应将递归改为非递归，即采用循环方法来解决同一问题。如果一个函数中所有递归形式的调用都出现在函数的末尾，则称这样的递归为尾递归。尾递归可以容易地改为迭代过程。因为当递归调用返回时，总是返回上一层递归调用语句的下一句语句处，在尾递归的情况下，正好返回函数的末尾，因此不再需要利用栈来保存返回地址，大多数现代的编译器会利用这种特点自动生成优化的代码。。

//普通递归
public static long fib_1(int n){
    if(n<=1){
        return 1;
    }
    return fib_1(n-1)+fib_1(n-2);
}

//尾递归
public static long fib_2(int n){
    return fib_iter(1,1,n);
}

public static long fib_iter(long a,long b,int n){
    if(n<=0){
        return a;
    }
    return fib_iter(b,a+b,n-1);
}

//for循环
public static long fib_3(int n){
    if(n<=1){
        return 1;
    }else{
        long fib=0;
        long a=1;
        long b=1;
        for(int i=1;i<n;i++){
            fib=a+b;
            a=b;
            b=fib;
        }
        return fib;
    }
}

递归设计法则

当编写递归例程的时候，关键要牢记递归的四条基本法则。

（1）基准情形。必须有一些基准情形，它无须递归就能够解出。

（2）不断推进。对于那些需要递归求解的情形，每一次递归调用都必须要使求解情况朝接近基准情形的方向推进。

（3）设计法则。假设所有的递归调用都能运行。

（4）合成效益法则(compound interest rule)。在求解一个问题的同一实例时，切勿在不同的递归调用中做重复性的工作。

队列

定义：队列是限定只能在表的一端进行插入，在表的另一端进行删除的线性表

队尾(tail)——允许插入的一端

队头(head )——允许删除的一端

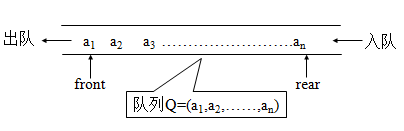
队列ADT

queue_new：建立一个空队列。

queue_free：清除一个队列，并释放内存。

queue_is_empty：若队列空，则返回1；否则返回0。

queue_is_full：若队列满，则返回1；否则返回0。

queue_peek_head：返回队头元素。

queue_in：在队尾插入元素x。

queue_out：从队列中删除队头元素，并返回队头元素。

queue_clear：清除队列中全部元素。

queue_length：返回队列的长度。

顺序队

与线性表、栈类似，队列也有顺序存储和链式存储两种存储方法。

顺序存储的队称为顺序队。因为队的队头和队尾都是活动的，因此，除了队列的数据区外还有队头、队尾两个指针。顺序队的类型定义如下：

＃define MAXSIZE 1024   /*队列的最大容量*/
typedef struct {
    datatype data[MAXSIZE];  /*队员的存储空间*/
    int tail,head ;  /*队头、队尾指针*/
} SeqQueue;

顺序队操作

设队头指针指向队头元素前面一个位置，队尾指针指向队尾元素（这样的设置是为了某些运算的方便，并不是唯一的方法）。

置空队则为：sq->head =sq->tail= -1;

在不考虑溢出的情况下，入队操作队尾指针加1，指向新位置后，元素入队。操作如下：

sq->tail++;
sq->data[sq->tail]=x;  /*原队头元素送x中*/

在不考虑队空的情况下，出队操作队头指针加1，表明队头元素出队。操作如下：

sq->head ++;
x = sq->data[sq->head ];

队中元素的个数：m = (sq->tail)-(q->head );

队满时：m = MAXSIZE;

队空时：m = 0;

顺序队操作图例

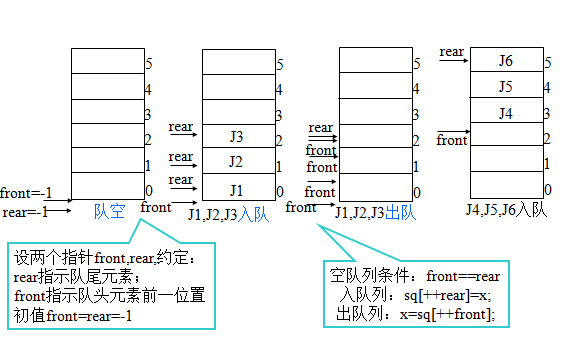
存在问题

设数组维数为M，则：

当 \(head =-1\) , \(tail=M-1\) 时，再有元素入队发生溢出——真溢出

当 \(front≠-1\) , \(tail=M-1\) 时，再有元素入队发生溢出——假溢出

解决方案

队首固定，每次出队剩余元素向下移动，问题：效率低下。

循环队列

基本思想：把队列设想成环形，让sq[0]接在sq[M-1]之后，若rear+1==M,则令rear=0;

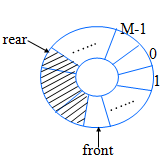
实现：利用“模”运算

入队: \(tail = (tail+1)\%M\) ; \(sq[tail] = x\);

出队: \(head = (head+1)\%M\) ; \(x = sq[head]\) ;

队满队空判定条件

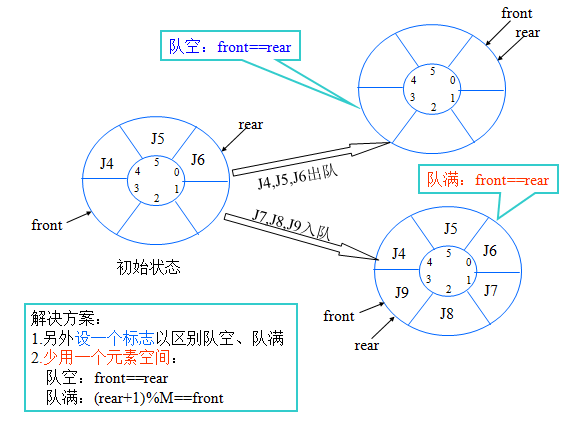
循环队列实现

下面的循环队列及操作按第一种方法实现。

循环队列的类型定义如下：

struct _CirQueue {
    CirQueueValue data[MaxQueueSize];   /* 定义存放队列元素的数组 */
    int head;   /* 指示队首下标 */
    int tail;   /* 指示队尾下标 */
};

循环队列_置空队

置空队

CirQueue *cirqueue_new(void){
    int i;
    CirQueue *cirqueue;
    cirqueue = (CirQueue *)malloc(sizeof(CirQueue));    /* 为队列结构分配内存 */
    for(i = 0; i < MaxQueueSize; i++)
        cirqueue->data[i] = NULL;   //data初始化为空指针 
    cirqueue->head = cirqueue->tail = -1;
    return cirqueue;
}
  

循环队列_入队

入队操作队尾指针加1，指向新位置后，元素入队。操作如下：

int cirqueue_in(CirQueue *cirqueue, CirQueueValue data){
    if(cirqueue_is_full(cirqueue))
        return 0;   //数组已满则返回0
    cirqueue->tail = (cirqueue->tail + 1) % MaxQueueSize;   /* 队尾下标+1并取对MaxQueueSize的余数 */
    cirqueue->data[cirqueue->tail] = data;
    return 1;
}

循环队列_出队

出队操作队头指针加1，表明队头元素出队。操作如下：

CirQueueValue cirqueue_out(CirQueue *cirqueue){
    CirQueueValue result;
    if (cirqueue_is_empty(cirqueue))
        return NULL;    //队列为空则返回空指针
    result = cirqueue->data[(cirqueue->head + 1) % MaxQueueSize];
    cirqueue->head = (cirqueue->head + 1) % MaxQueueSize;   /* 队首下标+1并取对MaxQueueSize的余数 */
    return result;
}

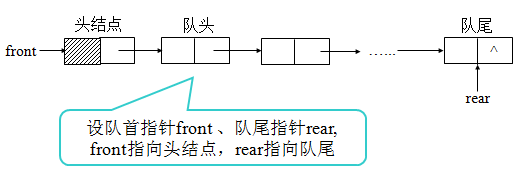
链队

链式存储的队称为链队。和链栈类似，用单链表来实现链队，根据队的FIFO原则，为了操作上的方便，我们分别需要一个头指针和尾指针，如下图所示。

舞伴问题

舞伴问题的描述：假设在周末舞会上，男士们和女士们进入舞厅时，各自排成一队。跳舞开始时，依次从男队和女队的队头上各出一人配成舞伴。若两队初始人数不相同，则较长的那一队中未配对者等待下一轮舞曲。

在算法中，假设男士和女士的记录存放在一个数组中作为输入，然后依次扫描该数组的各元素，并根据性别来决定是进入男队还是女队。当这两个队列构造完成之后，依次将两队当前的队头元素出队来配成舞伴，直至某队列变空为止。此时，若某队仍有等待配对者，算法输出此队列中等待者的人数及排在队头的等待者的名字，他（或她）将是下一轮舞曲开始时第一个可获得舞伴的人。

用队列实现舞伴问题的模拟

代码：

#include <stdio.h>
#include "lqueue.h"

/* 记录人物信息的结构 */
typedef struct {
    char name[20];
    char sex;   /* "M""F"分别表示男士和女士 */
}Person;

/* 对数组进行舞伴配对 */
void dance_partner(Person dancer[], int num) {
    ListEntry *malelist = NULL, *femalelist = NULL;
    Person *person;
    int i;
    /* 将数组中的人物信息加入队列 */
    for (i = 0; i <= num - 1; i++) {
        person = &dancer[i];
        if(dancer[i].sex == 'F')
            lqueue_in(&femalelist, person); /* 女士加到队尾 */
        else
            lqueue_in(&malelist, person);   /* 男士加到队尾 */
    }
    printf("The dancing partner are: \n\n");
    /* 每次男女队头人物配对，输出名字并从队列移除，直到某一队为空 */
    while (!lqueue_is_empty(femalelist) && !lqueue_is_empty(malelist)) {
        person = lqueue_out(&malelist); /* 队首男士离开队列 */
        printf("%s \t", person->name);
        person = lqueue_out(&femalelist);   /* 队首女士离开队列 */
        printf("%s\n", person->name);
    }
    /* 输出剩下的队列中的人数以及队首人物名字 */
    if (!lqueue_is_empty(femalelist)) {
        printf("\nThere are %d women waiting for the next round.\n", lqueue_length(femalelist));
        person = lqueue_peek(femalelist);
        printf("%s will be the first to get a partner. ", person->name);
    }
    else if (!lqueue_is_empty(malelist)) {
        printf("\nThere are %d men waiting for the next round.\n", lqueue_length(malelist));
        person = lqueue_peek(malelist);
        printf("%s will be the first to get a partner.", person->name);
    }
}

int main(void){
    Person dancer[] = {{"Rose", 'F'}, {"Bill", 'M'}, {"James", 'M'}, {"Andy", 'M'}, 
                        {"Mike", 'M'}, {"Jane", 'F'}, {"Jack", 'M'}, {"Amy", 'F'}};
    dance_partner(dancer, 8);
    return 0;
} 

队列的应用

队列应用非常广泛。凡是需保留待处理的数据，并且符合先进先出原则的，都可以使用队列结构，如本书后面将介绍的图的广度优先搜索程序。操作系统中很多地方都用到队列，比如作业调度、I/O管理等。

上机实验

编写一个计算器，使之具有：

• 能够处理小数
• 能够处理求余运算符（%）
• 能够处理单目运算符，例如乘方（^）
• 能够处理负数（选做）
• 能够处理exp,sin,cos,tan,ctan等常见函数（选做）