数据结构与算法
线性表
2017年春
本次课内容
我们要学习最基本、最简单、也是最常用的一种数据结构——线性表。我们说“线性”和“非线性”,只在逻辑层次上讨论,而不考虑存储层次。在数据结构逻辑层次上细分,线性表可分为一般线性表和受限线性表。一般线性表也就是我们通常所说的“线性表”,可以自由的删除或添加结点。受限线性表是指结点操作受限制的线性表,例如栈和队列。
- 抽象数据类型的概念
- 线性表的抽象数据类型
- 顺序表的简单数组实现
- 顺序表的改进方式
- 链表的思想
- 单链表实现
- 双向链表和循环链表
抽象数据类型
数据类型(data type)在数据结构中的定义是一个值的集合以及定义在这个值集上的一组操作。例如,c语言中的int,其值的集合为某个区间上的整数(区间大小和编译器有关,在32位机器上一般占4个字节),定义在这个值集上的操作为加、减、乘、除、取模等算术运算。
引入数据类型的目的,是为了将用户不必了解的细节都封装起来,例如,用户在进行两个int变量求和操作时,既不需要了解int在计算机内部是如何表示的,也不需要知道其操作是如何实现的。
程序设计者注重的仅仅是“数学书求和”的抽象特征,而不是硬件上的“位”操作如何进行。
抽象数据类型(Abstract Data Type,ADT)是指一个数学模型和定义在该模型上的一组操作的集合。抽象数据类型主要是数学方面的抽象,并没有涉及到实现操作的具体步骤,也就是说ADT的定义取决于模型的逻辑特性,与其在计算机内部如何表示和实现无关,只要其数学特性不变,都不影响其外部的使用。
线性表的逻辑结构
线性表是最简单、最基本、也是最常用的一种线性结构。它有两种存储方法:顺序存储和链式存储,它的主要基本操作是插入、删除和检索等。
定义:线性表是具有相同数据类型的\(n\)(\(n\ge0\))个数据元素的有限序列,通常记为: \[ (a_1,a_2,\ldots,a_i,\ldots,a_n) \] 其中:元素个数\(n\)为表长度,\(n=0\)时称为空表。当\(1<i<n\)时:
- \(a_i\)的直接前驱是\(a_{i-1}\),\(a_1\)无直接前驱
- \(a_i\)的直接后继是\(a_{i+1}\),\(a_n\)无直接后继
例1: 英文字母表(A, B, C, … , Z)是一个线性表
例2: 学生信息可以存储成一个线性表
| 学号 | 姓名 | 年龄 |
| 001 | 张三 | 18 |
| 002 | 李四 | 19 |
| ...... | ...... | ...... |
线性表ADT
list_is_empty:判断一个表是否为空表,空表返回非零值,非空返回零。
list_is_last:判断一个结点是否为表的尾结点,尾结点返回非零值,否则返回零。
list_free:释放整个表内存。
list_prepend:在表头插入结点。
list_append:在表尾插入结点。
list_next:获取表中下一个结点。
list_find:找到表中数据。
list_nth_data:获得表中的第n个数据。
list_data:返回结点中存储的数据。
list_length:得到表的长度,返回链表中结点的个数。
list_remove:删除一个结点,成功删除返回非零数,结点不存在返回零。
list_insert:向表中插入结点。顺序表
顺序表定义:线性表的顺序存储是指在内存中用地址连续的一块存储空间顺序存放线性表的各元素,用这种存储形式存储的线性表称为顺序表。
元素地址计算方法:
\[ LOC(a_i)=LOC(a_1)+(i-1)*L \\ LOC(a_{i+1})=LOC(a_i)+L \]
其中:\(L\)为一个元素占用的存储单元个数,\(LOC(a_i)\)为线性表第\(i\)个元素的地址
特点:逻辑上相邻—物理地址相邻,随机存取
顺序表的简单数组实现
可用C语言的一维数组实现

线性表的一维数组实现
typedef int datatype; /* datatype可为任何类型, 这里假设为int */
#define MAXSIZE 1024 /* 线性表可能的最大长度*/
typedef struct {
/* 数据域data是存放结点的向量空间,第一个结点是data[0] */
datatype data[MAXSIZE];
int last;/* 数据域 last 表示线性表的终端结点在向量空间中的位置*/
} SeqList;定义一个线性表:
SeqList L;或
SeqList *L;顺序表上初始化
初始化
顺序表的初始化即构造一个空表,这对表是一个加工型的运算,因此,将L设为指针参数,首先动态分配存储空间,然后,将表中 last 指针置为-1,表示表中没有数据元素。
初始化算法
SeqList * seqlist_init( ) {
SeqList *L;
L = (SeqList *)malloc(sizeof(SeqList));
L->last= -1;
return L;
}顺序表插入运算
线性表的插入是指在表的第i个位置上插入一个值为 x 的新元素,插入后使原表长为 n的表: \[ (a_1, a_2, \ldots, a_{i-1}, a_i, a_{i+1}, \ldots, a_n) \] 成为表长为\(n+1\)的表: \[ (a_1,a_2,...,a_{i-1},x,a_i,a_{i+1},\ldots,a_n) 。 \] 其中,\(i\)的取值范围为\(1\le i \le n+1\)。
顺序表插入运算图示

插入元素算法
int seqlist_insert(SeqList *L,int i,datatype x) {
int j;
if (L->last==MAXSIZE-1) {/*表空间已满,不能插入*/
printf(“表满”);
return(-1);
}
if (i < 1 || i > L->last+2) {/*检查插入位置的正确性*/
printf(“位置错”);
return(0);
}
for(j = L->last; j >= i-1; j--)
L->data[j+1] = L->data[j]; /* 结点移动 */
L->data[i-1] = x; /*新元素插入*/
L->last++; /*last仍指向最后元素*/
return (1); /*插入成功,返回*/
}插入算法时间复杂度
顺序表上的插入运算,时间主要消耗在了数据的移动上,在第\(i\)个位置上插入\(x\),从\(a_i\)到\(a_n\)都要向下移动一个位置,共需要移动\(n-i+1\)个元素,而\(i\)的取值范围为: \(1\le i \le n+1\),即有\(n+1\)个位置可以插入。设在第\(i\)个位置上作插入的概率为\(p_i\),则平均移动数据元素的次数:
\[E_i=\sum_{i=1}^{n+1}P_i(n-i+1)\]
若认为
\[P_i=1/(n+1)\]
即为等概率情况,则 \[E_i=1/(n+1)\sum_{i=1}^{n+1}(n-i+1)=n/2\]
所以\(T(n)=O(n)\)
顺序表删除运算
线性表的删除运算是指将表中第\(i\)(\(1\le i \le n\))个元素从线性表中去掉,删除后使原表长为\(n\)的线性表: \[ (a_1,a_2,\ldots,a_i-1,a_i,a_i+1\ldots,a_n) \] 成为表长为\(n-1\)的线性表: \[ (a_1,a_2,\ldots,a_i-1,a_i+1\ldots,a_n) \]
顺序表删除运算图示
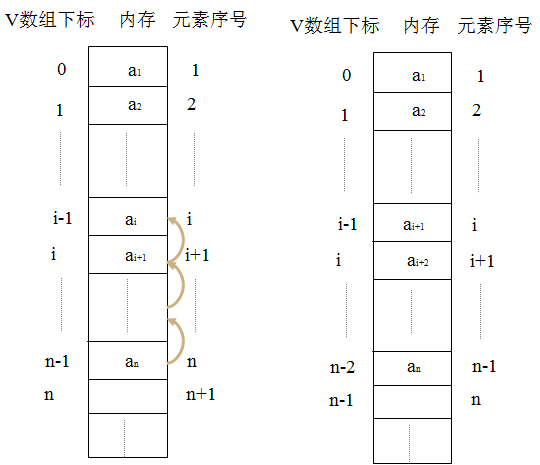
顺序表删除元素算法
int seqlist_remove(SeqList *L,int i) {
int j;
if(i < 1 || i > L->last+1) { /*检查空表及删除位置的合法性*/
printf (“不存在第i个元素”);
return(0);
}
for(j = i; j <= L->last; j++)
L->data[j-1] = L->data[j]; /*向上移动*/
L->last--;
return(1); /*删除成功*/
} 顺序表删除算法时间复杂度
与插入运算相同,其时间主要消耗在了移动表中元素上,删除第\(i\)个元素时,其后面的元素都要向上移动一个位置,共移动了\(n-i\)个元素,所以平均移动数据元素的次数: \[E_d=\sum_{i=1}^{n}P_i(n-i)\] 等概率情况下 \[P_i=1/n\] 则 \[E_d=1/(n)\sum_{i=1}^{n}(n-i)=(n-1)/2\] 所以\(T(n)=O(n)\)
顺序表按值查找
线性表中的按值查找是指在线性表中查找与给定值\(x\)相等的数据元素。在顺序表中完成该运算最简单的方法是:从第一个元素\(a_1\)起依次和\(x\)比较,直到找到一个与\(x\)相等的数据元素,则返回它在顺序表中的存储下标或序号(二者差一);或者查遍整个表都没有找到与\(x\)相等的元素,返回-1。
int seqlist_find(SeqList *L, datatype x) {
int i=0;
while(i<=L->last && L->data[i]!= x)
i++;
if (i>L->last)
return -1;
else
return i; /*返回的是存储位置*/
}改进的顺序表
下面要介绍的ArrayList是一种线性数据结构,它的底层是用数组实现的,与简单数组实现不同,它的容量能动态增长。ArrayList在保留数组可以快速查找的优势的基础上,弥补了数组在创建后,要往数组添加元素的弊端。
ArrayList要点
- ArrayList将保持基础数组,数组的容量,以及存储在ArrayList中的当前项数。
- ArrayList将提供一种机制以改变基础数组的容量。通过获得一个新数组,将老数组拷贝到新数组中来改变数组的容量,允许回收老数组。
- ArrayList将提供基本的例程,如arraylist_free、arraylist_clear和arraylist_sort等。还有不同的删除和插入操作,如果数组的大小和容量相同,那么插入操作将增加容量。
重要的结构体
typedef void * ArrayListValue; /* 指向数组中数据类型的指针. */
/* 动态数组结构,使用arraylist_new函数来创建新的动态数组. */
typedef struct _ArrayList ArrayList;
/* 定义动态数组结构. */
struct _ArrayList {
ArrayListValue *data; /* 数组的访问入口. */
unsigned int length; /* 数组中已存储的数据数. */
unsigned int _alloced; /* 数组的最大长度 */
};内存自动增长机制
ArrayList的内存自动增长是通过\(arraylist\_enlarge\)函数和判断过程实现的。\(arraylist\_enlarge\)函数可以实现将动态数组已分配的内存空间扩展为原来的2倍,整数\(newsize\)表示内存扩展后的数组长度,使用\(realloc\)函数对\(data\)重新进行内存分配,分配的空间大小等于\(newsize\)乘以结构\(ArrayListValue\)的大小,最后再使\(arraylist\)中的\(data\)指针指向新的空间\(data\),\(newsize\)赋值给_\(alloced\)。
static int arraylist_enlarge(ArrayList *arraylist){
ArrayListValue *data;
unsigned int newsize;
newsize = arraylist->_alloced * 2; /* 将已分配的数组内存空间扩展为原来的2倍 */
/* 给数组重新分配新的内存空间 */
data = realloc(arraylist->data, sizeof(ArrayListValue) * newsize);
if (data == NULL)
return 0;
else {
arraylist->data = data;
arraylist->_alloced = newsize;
return 1;
}
}ArrayList插入
/* 添加到指定位置的一般方法 */
int arraylist_insert(ArrayList *arraylist, unsigned int index,
ArrayListValue data){
if (index > arraylist->length) /* 检查下标是否越界 */
return 0;
if (arraylist->length + 1 > arraylist->_alloced) /* 必要时扩展数组长度 */
if (!arraylist_enlarge(arraylist))
return 0;
/* 把待插入位置及之后的数组内容后移一位 */
memmove(&arraylist->data[index + 1],&arraylist->data[index],
(arraylist->length - index) * sizeof(ArrayListValue));
arraylist->data[index] = data; /*在下标为index的位置插入数据 */
++arraylist->length;
return 1;
}
int arraylist_append(ArrayList *arraylist, ArrayListValue data){
return arraylist_insert(arraylist, arraylist->length, data);
}
int arraylist_prepend(ArrayList *arraylist, ArrayListValue data){
return arraylist_insert(arraylist, 0, data);
}ArrayList的删除
void arraylist_remove_range(ArrayList *arraylist, unsigned int index,
unsigned int length){
/* 检查范围是否合法 */
if (index > arraylist->length || index + length > arraylist->length)
return;
/* 把移除范围之后数组的内容前移 */
memmove(&arraylist->data[index],&arraylist->data[index + length],
(arraylist->length - (index + length))
* sizeof(ArrayListValue));
arraylist->length -= length; /* 新数组的长度 */
}
void arraylist_remove(ArrayList *arraylist, unsigned int index){
arraylist_remove_range(arraylist, index, 1);
}使用ArrayList的注意点
程序中的\(arraylist\_append\)和\(arraylist\_prepend\)两种常用的插入操作,通过调用通用的插入函数\(arraylist\_insert\)而得以简单实现,。\(arraylist\_append\)是添加元素到表的尾部,\(arraylist\_prepend\)是添加元素到表的头部。
\(arraylist\_remove\)的部分操作类似于\(arraylist\_insert\),只是那些位于指定位置上或指定位置后的元素向低位移动一个位置。
插入操作可能要求增加容量,扩充容量的代价是非常昂贵的,因为它需要移动在指定位置上或指定位置后面的那些元素到一个更高的位置上。
如果容量被扩充,那么它就要变成原来大小的两倍,以避免不得不再次改变容量,除非大小急剧地增加(这是要避免的,因此初始化的默认大小是很关键的参数)。
2.3 线性表的链式存储及运算实现
顺序表进行数组元素的插入和删除操作时,会引起大量数据的移动,从而使简单的数据处理变得非常复杂,低效,为了能有效地解决这些问题,一种称为“链表”的数据结构应运而生。链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。指针域记录了下一个数据的地址,有了这个地址之后,所有的数据就像一条链子一样串起来了。
数据域:元素本身
指针域:指示直接后继的存储位置

链表的特点
通过“链”建立起数据元素之间的逻辑关系,因此对线性表的插入、删除不需要移动数据元素,只需要修改“链”。因此,链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。
链表允许插入和移除表上任意位置上的节点,但是失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
链表有很多种不同的类型:单向链表,双向链表以及循环链表。
单链表
用一组任意的存储单元存储线性表的数据元素 利用指针实现了用不相邻的存储单元存放逻辑上相邻的元素
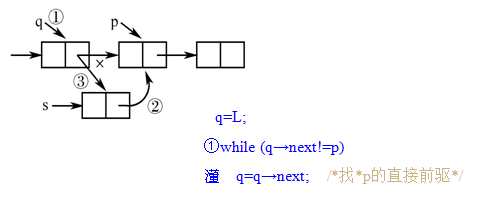
单链表的删除结点操作可以通过修改一个指针来实现。图给出在原表中删除第三个元素的结果。

插入操作需要使用一次\(malloc\)调用系统得到一个新单元(后面将详细论述)并在此后执行两次指针调整。其一般想法在图中给出,其中的虚线表示原来的指针。

单链表实现
typedef struct _SListEntry SListEntry; /* 单链表结构 */
/* 这里利用到了void指针,表示SListValue可以是任意数据类型,例如int、float或自定义结构体。 */
typedef void *SListValue; /* 指向链表中存储的数据的指针。 */
/* 单链表结点结构 */
struct _SListEntry {
SListValue data;
SListEntry *next;
};上面定义的SListEntry是结点的类型,定义一个单链表:
SListEntry* p;当\(p\)有定义时,值要么为NULL(表示一个空表),要么为第一个结点的地址(即链表的头指针)。
单链表图示
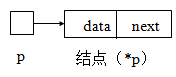
(*p)表示p所指向的结点
(*p).data或者p->data表示p指向结点的数据域
(*p).next或者p->next表示p指向结点的指针域
生成一个 SListEntry 类型新结点:
\(p=(SListEntry*)malloc(sizeof(SListEntry))\)
系统回收p结点:
free(p)
单链表插入操作
/* 在结点listentry之后插入一个新的结点,返回新结点的指针 */
SListEntry* slist_insert(SListEntry* listentry, SListValue data) {
SListEntry *newentry;
newentry = (SListEntry *)malloc(sizeof(SListEntry));
if(newentry == NULL)
return NULL;
newentry->data = data;
newentry->next = listentry->next;
listentry->next = newentry;
return newentry;
}单链表删除操作
/* 删除一个表中的特定结点,删除成功返回1,否则返回0 */
int slist_remove_entry(SListEntry **list, SListEntry *entry){
SListEntry *rover;
/* 如果链表或待删除结点为空,返回0 */
if (*list == NULL || entry == NULL)
return 0;
/* 删除头结点需要不同操作 */
if (*list == entry)
/* 更新链表头指针,并断开头结点 */
*list = entry->next;
else {
/* 搜索链表寻找前驱结点 */
rover = *list;
while (rover != NULL && rover->next != entry)
rover = rover->next;
if (rover == NULL)
return 0; /* 未找到 */
else
/* rover->next现在指向entry, 所以rover是前驱结点,entry从链表中脱离 */
rover->next = entry->next;
}
free(entry); /* 释放结点内存 */
return 1; /* 操作成功 */
}求表长
unsigned int slist_length(SListEntry *list) {
SListEntry *entry;
unsigned int length;
length = 0;
entry = list;
while (entry != NULL) {
/* 计算结点的数量 */
++length;
entry = entry->next;
}
return length;
}
查找
typedef int (*SListEqualFunc)(SListValue value1, SListValue value2);
SListEntry* slist_find_data(SListEntry* list,
SListEqualFunc callback,
SListValue data) {
SListEntry* rover;
/* 遍历链表,直到找到存有指定数据的结点 */
for (rover=list; rover != NULL; rover=rover->next) {
if (callback(rover->data, data) != 0) {
return rover;
}
}
/* 未找到 */
return NULL;
}单链表查找的效率
以上讨论的单链表的结点中只有一个指向其后继结点的指针域 \(next\) ,因此若已知某结点的指针为 \(p\) ,其后继结点的指针则为 \(p->next\) ,而找其前驱则只能从该链表的头指针开始,顺着各结点的 \(next\) 域进行,也就是说找后继的时间性能是 \(O(1)\),找前驱的时间性能是 \(O(n)\) 。
双向链表
从某个结点出发只能顺指针往后寻查其他结点。若要巡查结点的直接前趋,则需从表头指针出发。为了克服单链表这种单向性的缺点如果也希望找前驱的时间性能达到 O(1),则只能付出空间的代价:每个结点再加一个指向前驱的指针域,结点的结构为下图所示,用这种结点组成的链表称为双向链表。
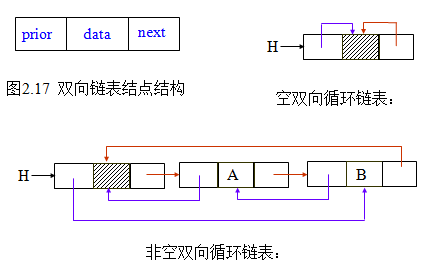
双向链表增加了一个附加的链,增加了对空间的需求,同时也使得插入和删除的运行时间增加了一倍,因为有更多的指针需要定位。另一方面,它却简化了删除操作,因为使用一个指向前驱元的指针来访问关键字就不是必须的,这些信息是都是现成的。
循环链表
对于单链表而言,最后一个结点的指针域是空指针,如果将该链表头指针置入该指针域,则使得链表头尾结点相连,就构成了单循环链表。如下图所示。
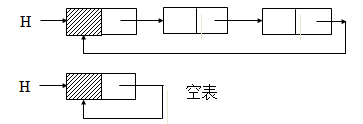
在单循环链表上的操作基本上与非循环链表相同,只是判断链表尾结点的方向不同,将原来判断指针是否为NULL变为是否是头指针,没有其它较大的变化。
循环链表的特点
循环链表的特点是无须增加存储量,仅对表的链接方式稍作改变,即可使得表处理更加方便灵活。
若在循环链表中设立尾指针而不设立头指针(如图(a)所示),可使某些操作简化。例如将两个线性表合并成一个表时,仅需将一个表的表尾和另一个表的表头相接。这个操作仅需改变两个指针值即可,运算时间为\(O(1)\)。
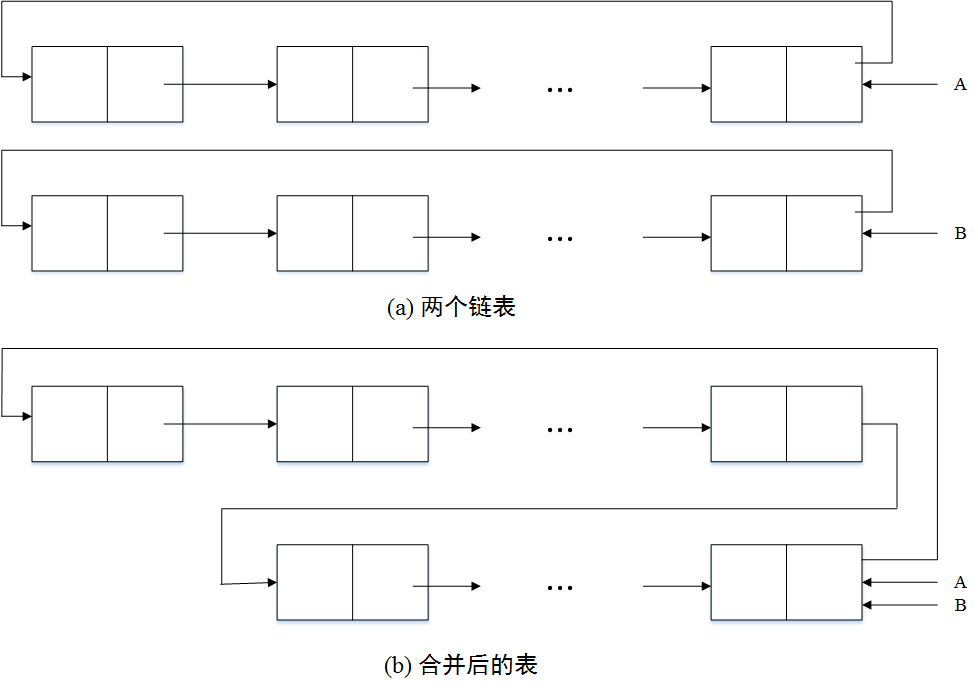
一元多项式
符号多项式的操作,已经成为表处理的典型用例。在数学上,一个一元多项式\(P_{n}(x)\)可按升幂写成:
\[P_{n}(x)=p_{0}+p_{1}x+p_{2}x^{2}+\cdots+p_{n}x^{n}\]
它由\(n+1\)个系数惟一确定。因此,在计算机里,它可用一个线性表\(P\)来表示:
\[P=(p_{0},p_{1},p_{2},\cdots,p_{n})\]
每一项指数\(i\)隐含在其系数\(p_{i}\)的序号里。
顺序表表示一元多项式
假设\(Q_{m}(x)\)是一元\(m\)次多项式,同样可以用线性表\(Q\)来表示:
\[Q=(q_{0},q_{1},q_{2},\cdots,q_{n})\]
不失一般性,设\(m<n\),则两个多项式相加的结果,\(R_{n}(x)=P_{n}(x)+Q_{m}(x)\),可用线性表\(R\)表示:
\[R=(p_{0}+q_{0},p_{1}+q_{1},p_{2}+q_{2},\cdots,p_{n}+q_{n})\]
显然,我们可以对\(P\)、\(Q\)和\(R\)采用顺序存储结构,使得多项式相加的算法定义十分简洁。至此,一次多项式的表示及相加问题似乎已经解决。
ArrayList实现一元多项式
在通常的应用中,多项式的次数可能很高且变化很大,使得顺序存储结构的最大长度很难确定。ArrayList具有自动扩展占用内存的特点,可以用来存储长度任意的多项式。
一元多项式相加:
void polynomial_add(ArrayList *poly1, ArrayList *poly2, ArrayList **polySum) {
int i, l;
//取poly1和poly2最高次数的较大者为相加后的最高次数
l = poly1->length;
if(poly2->length > poly1->length)
l = poly2->length;
*polySum = arraylist_new(l);
//分配内存空间
for(i = 0; i < l; i++){
(*polySum)->data[i] = (double *)malloc(sizeof(double));
*((double *)(polySum->data[i])) = 0; //初始化
}
// 开始做加法
for(i = 0; i < l; i++)
*(double *)((*polySum)->data[i]) = *(double *)(poly1->data[i]) + *(double *)(poly2->data[i]);
}一元多项式乘法
void polynomial_mult(ArrayList *poly1, ArrayList *poly2, ArrayList **polyMult) {
int i, j, l;
l = (poly1->length-1) + (poly2->length-1) + 1; //poly1和poly2的最高次数之和为相乘后的最高次数
(*polyMult) = arraylist_new(l);
for(i = 0; i < (*polyMult)->_alloced; i++) {
(*polyMult)->data[i] = (double *)malloc(sizeof(double));
*((double *)(polyMult->data[i])) = 0; //初始化
}
for(i = 0; i < poly1->length; i++)
for(j = 0; j < poly2->length; j++)
*(double *)((*polyMult)->data[i+j]) += *(double *)(poly1->data[i]) * *(double *)(poly2->data[j]);
}忽略将输入多项式初始化为零的时间,则乘法例程的运行时间与两个输入多项式的次数的乘积成正比。它适用于大部分项都有的稠密多项式。但如果\(P_{1}(X)=10X^{1000}+5X^{14}+1\)且\(P_{2}(X)=3X^{1990}-2X^{1492}+5\),那么运行效率就不高了。可以看出,大部分的时间都花在了乘以0和单步调试这两个输入多项式大量不存在的部分上,这是我们不愿意看到的。
链表表示一元多项式
针对上述问题,可使用单链表(slist)实现多项式。多项式的每一项含在一个单元中,并且这些单元以次数递减的顺序排序。
typedef struct _PolyNode PolyNode;
struct _PolyNode {
int coefficient; //系数
int exponent; //指数
};
typedef SListEntry *PolyList;链表实现的一元多项式相加
void polynomial_add(PolyList poly1, PolyList poly2, PolyList *polySum) {
PolyList p, q, head = NULL;
PolyNode *newnode;
p = poly1;
q = poly2;
while(p != NULL && q != NULL){ //两个多项式链表均还有数据
newnode = (PolyNode *)malloc(sizeof(PolyNode));
//指数相等则系数相加,存入新多项式中
if(((PolyNode *)p->data)->exponent == ((PolyNode *)q->data)->exponent) {
newnode->coefficient = ((PolyNode *)p->data)->coefficient + ((PolyNode *)q->data)->coefficient;
newnode->exponent = ((PolyNode *)p->data)->exponent;
p = p->next;
q = q->next;
}
//指数不相等则先存入指数较大的项
else if(((PolyNode *)p->data)->exponent > ((PolyNode *)q->data)->exponent) {
newnode->coefficient = ((PolyNode *)p->data)->coefficient;
newnode->exponent = ((PolyNode *)p->data)->exponent;
p = p->next;
}
else {
newnode->coefficient = ((PolyNode *)q->data)->coefficient;
newnode->exponent = ((PolyNode *)q->data)->exponent;
q = q->next;
}
if(newnode->coefficient == 0) { //系数为0的项不存储
free(newnode);
continue;
}
slist_prepend(&head, newnode);
}
//仅多项式A还有剩余数据
while(p != NULL) {
newnode = (PolyNode *)malloc(sizeof(PolyNode));
newnode->coefficient = ((PolyNode *)p->data)->coefficient;
newnode->exponent = ((PolyNode *)p->data)->exponent;
p = p->next;
slist_prepend(&head, newnode);
}
//仅多项式B还有剩余数据
while(q != NULL) {
newnode = (PolyNode *)malloc(sizeof(PolyNode));
newnode->coefficient = ((PolyNode *)q->data)->coefficient;
newnode->exponent = ((PolyNode *)q->data)->exponent;
q = q->next;
slist_prepend(&head, newnode);
}
*polySum = head;
}线性表作业
本章作业及实验内容:
- 实现完整的ArrayList程序
- 实现完整的单链表的程序
- 实验内容:使用链表实现一元多项式的表示、加法和乘法
要求:每个函数必须有测试