智能配电网络建模与分析
配电网重构与供电能力分析
2020年
本次课内容
在本次课中,我们将要学到:
- 配电网重构的概念和凸优化模型
- 配电网N-1校验的概念和计算方法
- 配电网供电能力分析的概念和计算方法
配电网重构的概念
自从20世纪80年代后期,配电网重构因在降低网络损耗、提高系统运行经济性和安全性方面具有显著效益而逐渐受到国内外学者广泛的关注。
配电网中的开关一般可分为两类:常闭的分段开关和常开的联络开关。分段开关安装在两段线路之间,将一条长线路分成许多线路段;联络开关负责联络两个主变电站、两条主馈线或环路形式的分支线路。这两种开关主要起两方面作用:
(1)在配电网正常运行时,通过改变开关的开闭状态重新设计网络拓扑结构,从而达到降低网络损耗、改善电压分布等目标;
(2)当线路发生故障时,迅速断开故障线路两端的分段开关将故障隔离,通过闭合联络开关将非故障线路上的失电负荷转移到其他线路,从而缩小停电范围、提高供电可靠性。
与此相对应,配电网重构也分为两种类型:优化重构和故障恢复重构。
- 优化重构是指在满足配电网运行约束的前提下,通过改变分段开关和联络开关的开闭状态来改变配电网的拓扑结构,从而达到特定的目标,如降低网络损耗、改善电压分布、均衡线路负载等。
- 故障恢复重构是指当配电网某处发生故障导致部分区域停电后,将受影响的非故障线路上的负荷通过联络开关转移到其他线路,从而对停电负荷恢复供电,其主要目的是恢复尽可能多的受故障影响而停电的负荷。
配电网N-1安全校验的概念
配电网\(N-1\)准则要求配电网中任意设备故障时,可以通过分段/联络开关实现故障隔离,并通过馈线有效联络实现负荷转供,实现对负荷持续良好供电。
配电网\(N-1\)安全分析可提高配电网在正常或检修时的抗干扰能力,提高用户用电质量,可有效反映配电网的坚强程度。同时,配电网\(N-1\)安全分析对配电网的合理规划具有重要指导意义,可优化配电网网架建设,带来可观的经济效益。
现有的负荷转供算法大致可分为启发式搜索算法、随机优化算法、专家系统法、混合算法和混合整数线性规划算法等五类。
启发式搜索算法。启发式算法可有效缩小解空间,适应各种结构不同的网络,但解的质量依赖于网络初始状态,随着配电网络复杂度的提高,设计合理的启发式规则较为困难。
随机优化算法。随机优化算法采用较完善的配电网供电恢复模型,利用寻优算法得到负荷转供的最优或次优方案,但迭代收敛较慢,计算时间较长,实时性差。
专家系统法。专家系统法模拟人类专家的决策过程,能够自动生成故障后负荷转供方案,实时性好,适用性广,但知识库的建立和集成耗时较长,且难以涵盖所有故障情况。
混合算法。结合以上算法的优缺点和适用范围,一些学者提出了混合算法。
混合整数线性规划算法。混合整数线性规划算法具有较好的收敛性和较快的计算速度。
配电网供电能力分析的概念
配电网的供电能力与输电网的输电能力指标对应。自2000年以来,随着我国城乡电网的大规模建设改造,供电能力逐渐成为评价配电网规划建设水平的重要指标。目前,文献中所研究的供电能力一般是指配电网最大供电能力(Total Supply Capability, TSC)。TSC是指在一定供电区域内,配电网满足\(N-1\)安全准则的条件下,考虑变电站与馈线转供能力和实际运行约束下的最大负荷供应能力,其定义如下:
设所研究供电区域的配电网络中有\(N_c\)个元件,当第\(i\)个元件因检修或故障退出运行后,考虑变电站与馈线转供能力和实际运行约束后,可以提供的最大负荷为\(A_i^{\max}\),则该配电网络的最大供电能力\(TSC\)为
\[\begin{equation} TSC = \min \left\{ {A_1^{\max },A_2^{\max }, \cdots ,A_{{N_c}}^{\max }} \right\} \end{equation}\]配电网供电能力的研究分析经历了如下3个阶段:
(1)以变电容量评估配电网供电能力阶段。
该阶段的评估方法以变电容载比法为典型。变电容载比主要反映变压器的备用容量,宏观上评估了配电网供电能力。但是,该方法未考虑配电网的网架结构与变电站联络对供电能力的影响,所得评估结果过于保守,不能全面评估配电网供电能力。
(2)考虑网络供电能力的评估阶段。
该阶段的典型评估方法有最大负荷倍数法、重复潮流法、线性规划法和模糊评价法等。该类评估方法不仅考虑主站变压器的容量,同时计及配电馈线的容量,所得结果更加贴合实际,但仍未考虑实际网络联络结构对配电网供电能力的影响。
(3)计及配电网\(N-1\)准则,考虑主变、馈线容量和网络拓扑互联的评估阶段。
该阶段的评估方法考虑了配电网\(N-1\)安全约束和网络联络情况,得到的供电能力评估结果更为合理、可靠。
最优化问题简介
最优化问题是指在一定约束条件下,求解一个目标函数最大值(或最小值)的问题。最优化问题可按如下几种方式进行分类。
(1)按约束类型分类。在最优化问题中,根据是否有变量的约束条件,可以将优化问题分为无约束优化问题和约束优化问题。其中约束优化问题又可以分为等式约束问题、不等式约束问题和混合约束问题三类。
(2)按目标和约束函数类型分类。如果目标函数和所有的约束函数都为线性函数,则该问题为线性规划问题。相反,如果目标函数或任何一个约束函数为非线性函数,则该问题为非线性规划问题。
(3)按变量类型分类。对于最优化问题,如果所有变量的值域均为实数域,则为连续优化问题;如果所有变量只能取整数,则相应的最优化问题为整数规划;如果仅一部分变量限制为整数,则为混合整数规划问题。整数规划的一种特殊情形是0-1规划,其整数变量只能取0或1。
凸优化问题
在非线性优化问题中,一类比较特殊的问题是凸优化问题。在凸优化问题中,变量的可行域为凸集,即对于可行域中的任意两点,它们连线上的每个点都位于可行域内。此外,凸优化的目标函数也必须为凸函数,即满足:
\[\begin{equation} f(tx+(1-t)y) \leq tf(x)+(1-t)f(y) \end{equation}\]式中:\(f\)为凸函数;\(x\)和\(y\)为定义域上的任意两点;\(t\)为(0,1)上的任意常数。
凸优化问题具有如下性质:
(1)凸优化问题的任一局部极小点是全局极小点,且全体局部极小点的集合为凸集。
(2)当凸优化的目标函数为严格凸函数时,若存在最优解,则这个最优解一定是唯一的最优解。
因为凸优化具有上述较好的性质,因此在某种意义上凸优化相比一般的最优化问题更容易求解。
二阶锥规划
二阶锥规划是一类可行域为二阶锥的凸优化问题,能够使用内点法快速地求解。满足如下不等式的点集为二阶锥:
\[\begin{equation} ||{Ax} + {b} ||_2 \leq {c}^{{T}}{x} + {d} \end{equation}\]式中:\({A}\)为常矩阵;\({x}\)为变量构成的数组;\({b}\)、\({c}\)、\({d}\)为维数与变量数量相同的常向量。
接下来将通过数学规划的形式对配电网网络重构与故障恢复进行描述,由于严格的数学模型属于非线性非凸规划,较难求解,因此可以选择引入二阶锥凸松弛技术和线性化方法,将模型转为具有凸可行域的形式以便求解,下面将对此建立其混合整数二阶锥规划模型与混合整数线性规划模型。
网络重构的目标函数
主动配电网进行网络重构的目标有多种,如:降低网络有功损耗,降低系统一定时间段内能量损耗,使线路负载均衡,提高系统供电可靠性,及提高电压稳定性等。对应的优化目标函数如下:
(1)降低网络有功损耗
\[\begin{eqnarray} \label{cg1} \text{min}\sum_{(ij)\in \Phi _\text{l}}^{ }r_{ij}\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}} \end{eqnarray}\](2)降低系统在一段时间内的能量损耗
所考虑的时间尺度\(T\)可以是一日、一周、一年等,通常结合开关操作费用以最小化总的损耗成本,可表示如下:
\[\begin{eqnarray} \label{cg4} \text{min}(\sum_{t=1}^{T}\lambda _{t}P_{\text{loss},t}+\sum_{l=1}^{N_\text{k}}C_{l}(k_{l}) ) \end{eqnarray}\]式中:\(\lambda _{t}\)为第\(t\)时间段内单位能量消耗的费用系数,可用实时电价表示;\(P_{\text{loss},t}\)为第\(t\)时间段内的有功功率损耗;\(C_{l}(k_{l})\)表示第\(l\)个开关在所考虑的时间段内切换开关状态\(k_{l}\)次所需的费用;\(N_\text{k}\)为总的开关数目。
(3)均衡线路负载
为留出足够的安全裕度、保证供电质量,一般需要将负荷合理的分配到各个支路上,使线路负载均衡。可表示如下:
\[\begin{eqnarray} \label{cg5} \text{min}\sum_{(ij)\in \Phi _\text{l}}^{ }\frac{P_{ij}^{2}+Q_{ij}^{2}}{\overline{s}_{ij}^{2}} \end{eqnarray}\]式中:\(\overline{s}_{ij}\)为支路\(ij\)的视在功率限值。
(4)提高系统供电可靠性
配电系统的供电可靠性评价指标有很多,包括用户平均停电时间(AIHC)、用户平均停电次数(AITC)、平均停电缺供量(AENS)、故障停电平均持续时间(AID)和供电可靠率(SA)等。对于实际的主动配电网网络重构问题,要综合考虑网络损耗、开关操作次数、安全裕度和系统可靠度等多个指标。一般可根据重要等级和需求,对上述目标函数进行加权组合,也可以使用模糊理论对重构方案进行综合评价。
网络重构的约束条件
(1)辐射状拓扑约束
为保护整定和减小短路电流,一般要求配电网呈辐射状运行,即网络中不存在环状拓扑结构。上节课对配电网辐射状拓扑约束的数学描述方法进行了详细讨论,给出了基于网络潮流平衡约束、基于虚拟潮流、基于图的生成树、基于供电路径和基于供电环路的配电网辐射状约束描述方法。在配电网络重构中可选用其中的一种方法描述网络辐射状拓扑约束,本小节中选用基于网络潮流平衡约束的配电网辐射状约束描述方法。
(2)电压安全约束
\[\begin{eqnarray} \label{cg8} \underline{V_{i}}\leq V_{i}\leq \overline{V}_{i} \end{eqnarray}\]式中:\(\underline{V_{i}}\)和\(\overline{V}_{i}\)分别为节点\(n_i\)的电压幅值下限和上限。
支路容量约束
(3)支路容量约束
配电网络中每条线路都有一定传输容量,若实际传输电量过大,将使得电线严重发热,导致线路损耗增加且容易损伤输电线。线路容量可用视在功率平方\(\overline{s_{ij}}^{2}\)为限进行描述:
\[\begin{eqnarray} \label{cg9} P_{ij}^{2}+Q_{ij}^{2}\leq \overline{s_{ij}}^{2} \end{eqnarray}\]然而上式并不完善,如果支路\(ij\)断开,支路潮流\(P_{ij}\)和\(Q_{ij}\)应该为0,因此改进为
\[\begin{eqnarray} \label{cg10} P_{ij}^{2}+Q_{ij}^{2}\leq z_{ij} \overline{s_{ij}}^{2} \end{eqnarray}\]式中:\(z_{ij}\)为描述支路\(ij\)投切状态的二进制变量,为0时表示支路断开,为1时表示支路闭合。
支路潮流约束
有文献提出了辐射状配电网的DistFlow支路潮流方程,DistFlow支路潮流方程在线路模型中忽略了并联导纳,有利于提高计算效率。
\[\begin{gather} \sum_{k:(jk)\in\Phi_\text{l}}^{ }P_{jk}=\sum_{i:(ij)\in\Phi_\text{l}}^{ }(P_{ij}-r_{ij}\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}})-P_{j}^\text{L} \label{cg11}\\ \sum_{k:(jk)\in\Phi_\text{l}}^{ }Q_{jk}=\sum_{i:(ij)\in\Phi_\text{l}}^{ }(Q_{ij}-x_{ij}\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}})-Q_{j}^\text{L} \label{cg12}\\ V_{i}^{2}-V_{j}^{2}=2(r_{ij}P_{ij}+x_{ij}Q_{ij})-(r_{ij}^{2}+x_{ij}^{2})\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}} \label{cg13} \end{gather}\]式中:\(P_{j}^\text{L}\)和\(Q_{j}^\text{L}\)分别表示节点\(n_j\)处计及分布式电源出力的净流出有功和无功负荷。
对于网络重构而言,DistFlow潮流约束并不完善,仍存在三个问题需要解决。
零注入孤立节点的问题
零注入节点是指本身没有净注入功率的节点,即\(P_{j}^\text{L}\)和\(Q_{j}^\text{L}\)均为0,如下图所示。
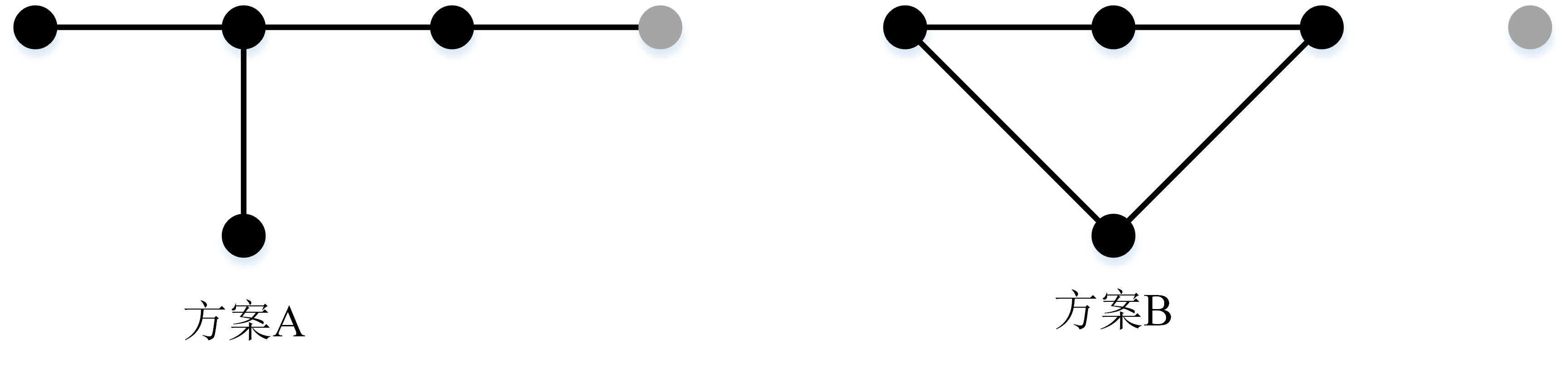
图中浅灰色节点表示零注入节点。重构方案A和B均满足辐射状约束式和潮流约束,但方案B中却出现了孤立节点和环状结构并存的情况,显然不符合要求。为防止这种情况存在,将式上述两式分别改进为
\[\begin{gather} \sum_{k:(jk)\in\Phi_\text{l}}^{ }P_{jk}=\sum_{i:(ij)\in\Phi_\text{l}}^{ }(P_{ij}-r_{ij}\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}})-P_{j}^\text{L},\ \ \left | P_{j}^\text{L} \right |\geq \delta \label{cg14}\\ \sum_{k:(jk)\in\Phi_\text{l}}^{ }Q_{jk}=\sum_{i:(ij)\in\Phi_\text{l}}^{ }(Q_{ij}-x_{ij}\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}})-Q_{j}^\text{L},\ \ \left | Q_{j}^\text{L} \right |\geq \delta \label{cg15} \end{gather}\]式中:\(\delta\)表示一个很小的正数。
支路断开的影响
倘若支路\(ij\)处于断开状态,约束条件式会将\(P_{ij}\)和\(Q_{ij}\)限制为0,而此时原式将会转变为\(V_{i}^{2}-V_{j}^{2}=0\),即强制不相连支路两端电压幅值相等,这是不合理的。对此引入大\(M\)方法,将原式转为如下形式:
\[\begin{eqnarray} \label{cg16} \left\{\begin{aligned} &m_{ij}=(1-z_{ij})\cdot M\\ &V_{i}^{2}-V_{j}^{2}\leq m_{ij}+2(r_{ij}P_{ij}+x_{ij}Q_{ij})-(r_{ij}^{2}+x_{ij}^{2})\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}}\\ &V_{i}^{2}-V_{j}^{2}\geq -m_{ij}+2(r_{ij}P_{ij}+x_{ij}Q_{ij})-(r_{ij}^{2}+x_{ij}^{2})\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}} \end{aligned}\right. \end{eqnarray}\]式中:\(M\)是一个很大的正数。
非凸形式的凸化处理
改进的三式均为强非凸形式,较难求解。为此引入二阶锥松弛技术,将原模型转化为一个MISOCP问题。
首先定义新优化变量——节点电压幅值的平方\(U_{i}\)和支路电流幅值的平方\(L_{ij}\)
\[\begin{gather} U_{i}=V_{i}^{2} \label{cg17}\\ L_{ij}=i_{ij}^{2}=\frac{P_{ij}^{2}+Q_{ij}^{2}}{V_{i}^{2}} \label{cg18} \end{gather}\]在模型中添加式两个新约束,用新变量代替原目标函数和约束条件中的对应项,并将支路容量约束式用电流幅值约束式替代。同时将式二松弛后等价变形为标准的二阶锥形式:
\[\begin{eqnarray} \label{cg21} \begin{Vmatrix} 2P_{ij}\\ 2Q_{ij}\\ L_{ij}-U_{i} \end{Vmatrix}_2 \leq L_{ij}+U_{i} \end{eqnarray}\]网络重构的MISOCP问题
(1)目标函数
\[\begin{eqnarray} \label{cg22} \underset{z_{ij}}{\text{min}}(\sum_{(ij)\in\Phi_\text{l}}^{ }r_{ij}L_{ij}) \end{eqnarray}\](2)约束条件
\[\begin{gather} \left\{\begin{matrix} \sum_{(ij)\in\Phi _{l}}^{ }z_{ij}=N-N_{\text{s}}\\ z_{ij}\in\left \{ 0,1 \right \},\forall (ij)\in\Phi_\text{l} \end{matrix}\right. \label{cg23}\\ \left\{\begin{matrix} \underline{V_{i}}\leq V_{i}\leq \overline{V}_{i}\\ L_{ij}\leq z_{ij}\overline{i_{ij}}^{2} \end{matrix}\right.\\ \begin{Vmatrix} 2P_{ij}\\ 2Q_{ij}\\ L_{ij}-U_{i} \end{Vmatrix}_2 \leq L_{ij}+U_{i} \end{gather}\]恢复控制的混合整数线性规划模型
由于配电网的辐射状运行,当系统发生故障并进行定位隔离后,故障点下游将出现非故障失电区,而故障恢复就是将这部分失电负荷通过网络重构转供到带电区域,以实现供电恢复。因此,恢复控制本质上是一个满足配电网运行约束下的最优开关组合选择问题,可以用数学规划的形式进行描述。
根据现有文献的研究成果,可以将恢复控制问题建模为一个混合整数二次约束规划(MIQCP)问题,其目标函数为最大化恢复失电负荷量,具体形式如下:
\[\begin{eqnarray} \label{Eps1} \text{max}\sum_{n_i \in \Psi _\text{out}}^{}\widetilde{P}_{i} \end{eqnarray}\]式中:\(\Psi _\text{out}\)为失电节点集合,\(\widetilde{P}_{i}\)为故障恢复期间节点\(n_i\)的实际有功负荷。模型以尽可能多地恢复失电负荷为目标,在实际中还可以考虑不同负荷的优先等级,将上式中的节点负荷变为\(\omega _{i}\widetilde{P}_{i}\),其中\(\omega _{i}\)为表征失电负荷重要性的权重因子。
模型约束
配电网辐射状约束如下:
\[\begin{eqnarray} \label{Eps2} \left\{\begin{matrix} \sum_{\left ( ij \right )\in \Phi _{l}}^{}z_{ij}=N-N_{\text{s}}\\ z_{ij}\in \left \{ 0,1 \right \},\forall\left ( ij \right )\in \Phi _\text{l} \end{matrix}\right. \end{eqnarray}\]式中:\(z_{ij}\)为描述支路\(ij\)投切状态的二进制变量;\(\Phi _\text{l}\)表示配电系统故障隔离后所有的支路集合;\(N\)和\(N_\text{s}\)分别表示故障隔离后的节点总数和电源节点数。
电压安全约束:
\[\begin{eqnarray} \label{Eps3} \left\{\begin{aligned} &U_{i}=V_{i}^{2}\\ &\underline{U_{i}} \leq U_{i} \leq \overline{U_{i}},\forall i\in \Psi _\text{b} \end{aligned}\right. \end{eqnarray}\]式中:\(\Psi _\text{b}\)为故障隔离后的所有节点集合;\(\underline{U_{i}}\)和\(\overline{U_{i}}\)分别为节点\(n_i\)的电压幅值平方的下限值和上限值。
线路容量约束:
\[\begin{eqnarray} \label{Eps4} P_{ij}^{2}+Q_{ij}^{2}\leq z_{ij}\overline{s}_{ij}^{2} \end{eqnarray}\]式中:\(P_{ij}\)和\(Q_{ij}\)分别表示支路\(ij\)流过的有功和无功功率,方向为从节点\(n_i\)流向节点\(n_j\);\(\overline{s}\)为支路\(ij\)的视在功率限值。
功率平衡约束:
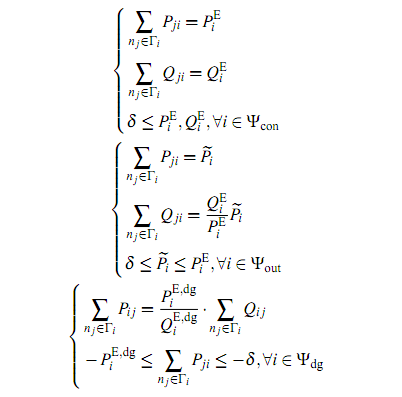
上述三式依次表示带电节点、失电节点和与分布式电源(DG)相连节点的功率平衡约束。式中:\(\Psi _\text{con}\),\(\Psi _\text{out}\),\(\Psi _\text{dg}\)分别表示故障隔离后带电节点集合、失电节点集合和DG节点集合;\(P_{i}^\text{E}\)和\(Q_{i}^\text{E}\)分别为节点\(n_i\)上预期的有功和无功负荷值;\(P_{i}^{\text{E},\text{dg}}\)和\(Q_{i}^{\text{E},\text{dg}}\)分别为DG节点\(n_i\)上预期的分布式电源有功和无功最大出力;\(\delta\)为一个很小的正数,用以防止零注入孤立节点的存在;\(\Gamma_i\)表示与节点\(n_i\)相连的节点集合。
潮流方程约束:
\[\begin{eqnarray} \label{Eps8} \left\{\begin{aligned} &m_{ij}=\left ( 1-z_{ij} \right )\cdot M\\ &U_i-U_j \leq m_{ij}+2\left ( P_{ij}r_{ij}+Q_{ij}x_{ij} \right )\\ &U_i-U_j \geq -m_{ij}+2\left ( P_{ij}r_{ij}+Q_{ij}x_{ij} \right )\\ &\forall \left ( ij \right )\in \Phi _\text{l} \end{aligned}\right. \end{eqnarray}\]式中:\(M\)为一个很大的正数,当\(z_{ij}=0\),即支路\(ij\)断开时,用以取消对应的潮流约束。同样,该式也忽略了网络功率损耗二次项。
以上就是配电网故障恢复的整个数学模型,从形式上看,它是一个混合整数二次约束规划。
二次约束的线性化处理
为了便于对偶化处理,需要对恢复控制模型进行线性化。而原模型的表达式中,除了二次约束条件式(),均为线性形式。对此,可以采用图所示的二次圆约束线性化方法,用多个旋转正方形约束对二次圆约束进行逼近。
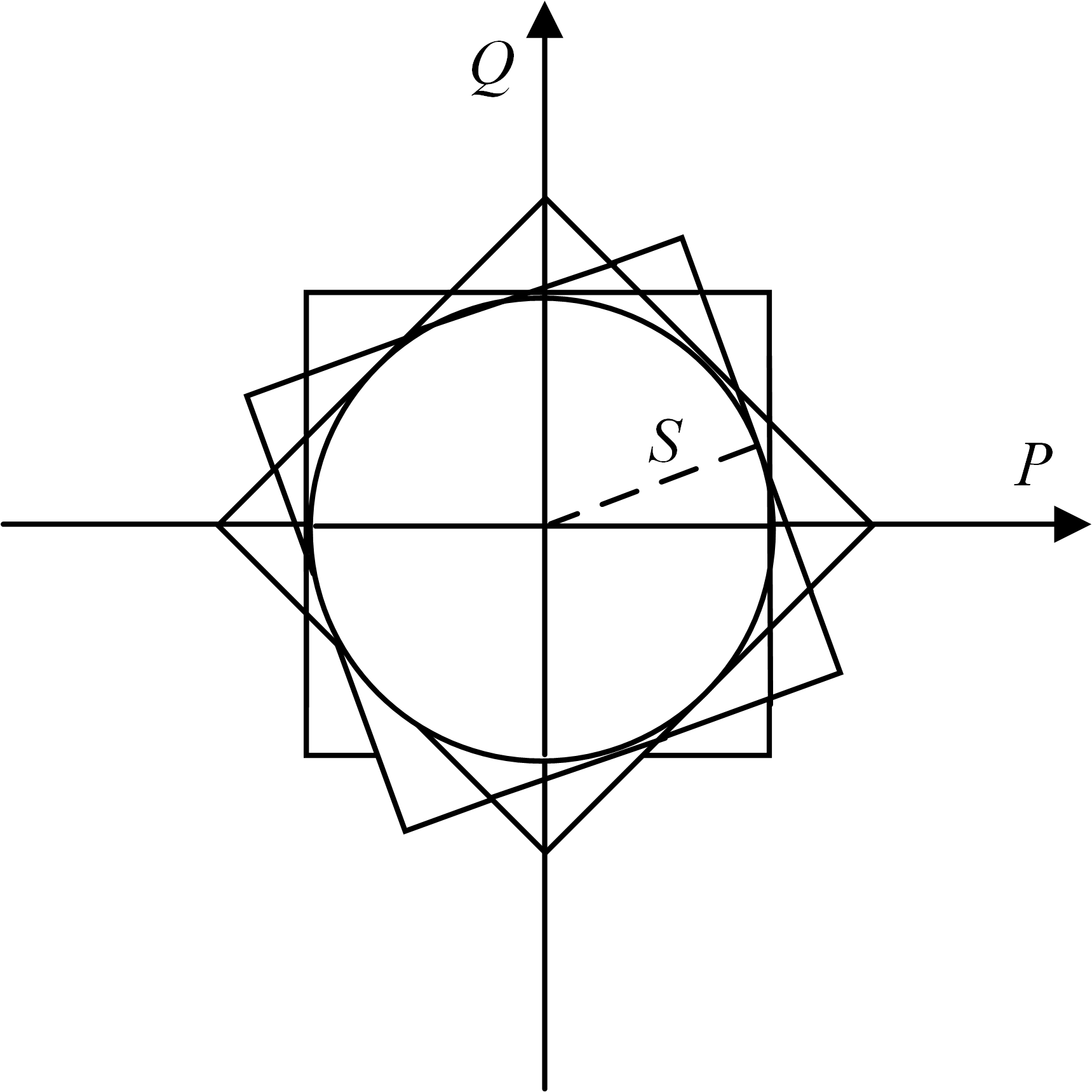
二次约束的线性化处理结果
可以看出,使用正方形约束越多,对二次约束逼近的精确度越高。在一般的工程应用中,使用两个呈45\(^{\circ}\)夹角的正方形约束就足够了精确了。因此,用线性形式代替,线路容量的约束变为如下所示:
\[\begin{eqnarray} \label{Eps9} \left\{\begin{aligned} &-z_{ij}\cdot \overline{s}_{ij}\leq P_{ij}\leq z_{ij}\cdot \overline{s}_{ij}\\ &-z_{ij}\cdot \overline{s}_{ij}\leq Q_{ij}\leq z_{ij}\cdot \overline{s}_{ij}\\ &-\sqrt{2}z_{ij}\cdot \overline{s}_{ij}\leq P_{ij}+Q_{ij}\leq \sqrt{2}z_{ij}\cdot \overline{s}_{ij}\\ &-\sqrt{2}z_{ij}\cdot \overline{s}_{ij}\leq P_{ij}-Q_{ij}\leq \sqrt{2}z_{ij}\cdot \overline{s}_{ij}\\ &\forall \left ( ij \right )\in \Phi _\text{l} \end{aligned}\right. \end{eqnarray}\]最终,配电网恢复控制优化模型转变为了一个混合整数线性规划(MILP)的形式。
配电网N-1安全校验
配电网\(N-1\)安全校验是衡量配电网运行可靠性的重要手段,\(N-1\)准则要求配电网任意位置发生故障时,可以实现故障隔离,并结合馈线联络方式通过改变开关运行状态,转供负荷至其他馈线,满足其用电需求。
在配电网\(N-1\)校验过程中,需要使用配电网重构技术判断失电负荷是否能成功转供,同时给出故障恢复的策略。本节在配电网\(N-1\)校验中重点考虑元件的过载,将无功功率、电压和网损等因素做简化处理。
在配电网规划中,一般以全年最大负荷作为\(N-1\)校验条件。配电网规模庞大,每个供电分区的供电范围通常较为明确,正常运行时一般不交叉、不重叠。因此,接下来以馈线组为单位,针对馈线组故障中最严重的情况馈线出口故障,进行配电网\(N-1\)安全校验分析。
配电网N-1安全校验数学模型
配电网\(N-1\)安全校验常用于配电网规划阶段,重点考虑元件是否过载,可对无功功率、电压和网损等因素做简化处理。
利用供电路径对该问题进行描述较为直观,因此本节以网络中所有供电路径的状态为变量,并采用上节课中基于供电路径的配电网辐射状约束描述方法描述配电网拓扑,建立配电网\(N-1\)安全校验的0-1线性规划模型。
优化目标
满足馈线\(N-1\)的负荷转供方案可能不止一个,在配电网实际运行中,开关装置动作需要一定的时间,为尽快恢复供电,本节采用基于动作开关数最少的原则确定负荷转供方案。
开关装置的动作与否可以用其所在支路的通断状态描述。为得到用路径状态表示支路通断状态的表达式,首先证明下述命题成立。
命题:设配电网络中支路\({b}\)两端的节点为\(n_i\)和\(n_j\),支路\({b}\)为通路的充要条件为经过该支路为负荷节点\(n_i\)、\(n_j\)供电的所有路径状态之和为1,即
\[\begin{equation} \sum_{\pi_{i,k}\in \Pi_{i,{b}}}W_{i,k}+\sum_{\pi_{j,k}\in \Pi_{j,{b}}}W_{j,k}=1 \label{Eps10} \end{equation}\]式中:\(\pi_{i,k}\)为负荷节点\(n_i\)的第\(k\)条可能供电路径;\(\Pi_{i,{b}}\)表示经过支路\({b}\)为负荷节点\(n_i\)供电的所有供电路径集合; \(W_{i,k}\) 为路径\(\pi_{i,k}\)的状态,若路径\(\pi_{i,k}\)连通为1,否则为0。
命题证明
充分性:命题成立可分为两种情况,即下述两式任一成立。
\[\begin{eqnarray} \label{Eps11} \left\{\begin{matrix} \sum_{\pi_{i,k}\in \Pi_{i,{b}}}W_{i,k}=0\\ \sum_{\pi_{j,k}\in \Pi_{j,{b}}}W_{j,k}=1 \end{matrix}\right. \end{eqnarray}\] \[\begin{eqnarray} \label{Eps12} \left\{\begin{matrix} \sum_{\pi_{i,k}\in \Pi_{i,{b}}}W_{i,k}=1\\ \sum_{\pi_{j,k}\in \Pi_{j,{b}}}W_{j,k}=0 \end{matrix}\right. \end{eqnarray}\]若式1成立,则说明负荷节点\(n_j\)的供电路径经过支路\({b}\),故支路\({b}\)为通路。同理可证,若式2成立,则支路\({b}\)为通路。因此,命题充分性得证。
必要性:若支路\({b}\)为通路,由配电网辐射状结构可知,支路\({b}\)中有电流且方向唯一。若电流从节点\(n_i\)流向节点\(n_j\),则式一成立;反之,式二成立。因此,命题必要性得证。
目标函数
设集合\(I_\text{s}\)表示原运行方式下联络开关所在支路的集合,集合\(D_\text{s}\)表示分段开关所在支路的集合。结合上述命题得基于开关数最优的目标函数如下式所示:
\[\begin{equation} \text{min}\{\sum_{b\in I_\text{s}}(\sum_{\pi_{i,k}\in \Pi_{i,b}}W_{i,k}+\sum_{\pi_{j,k}\in \Pi_{j,b}}W_{j,k})+\sum_{b\in D_\text{s}}(1-\sum_{\pi_{i,k}\in \Pi_{i,b}}W_{i,k}-\sum_{\pi_{j,k}\in \Pi_{j,b}}W_{j,k})\} \label{Eps13} \end{equation}\]式中:前一个求和式表示联络开关动作数,后一个求和式表示分段开关动作数。
约束条件
设某一馈线组网络中包含\(N\)个节点、\(N_\text{s}\)电源节点、\(B\)条支路,第\(i\)个负荷节点的负载量为\(L_i\),第\(j\)个电源节点的容量为\(S_j\),第\(m\)条支路的最大载流量为\(F_m\)。对任一条待\(N-1\)安全校验的馈线,经负荷转供后,重构网络需满足下述两式,即网络为辐射状。
\[\begin{equation} \sum_{\pi_{i,k}\in \Pi_{i}}W_{i,k}=1, \quad \forall i \label{8-12} \end{equation}\] \[\begin{equation} W_{i,k}\leq W_{l,m}, \quad \forall \pi_{l,m}\subset \pi_{i,k} \label{8-13} \end{equation}\]同时应满足以下约束条件:
\[\begin{gather} \sum_{\pi_{i,k}\in \Pi_{S,j},\pi_{i,k}\in \Pi_{i}}W_{i,k}L_i \leq S_j \label{Eps14}\\ \sum_{\pi_{i,k}\in \Pi_{B,m},\pi_{i,k}\in \Pi_{i}}W_{i,k}L_i \leq F_m \label{Eps15} \end{gather}\]式中:\(i=1,2,\cdots,N-N_\text{s}\);\(j=1,2,\cdots,N_\text{s}\);\(m=1,2,\cdots,B\)。
式1为电源容量约束,表示由第\(j\)个电源供电的所有负荷的负载量之和不超过该电源容量。式2为馈线载流量约束,表示第\(m\)条支路的实际载流量不超过其最大值。
配电网N-1安全校验流程
对于任意一个待校验配电网网络,其\(N-1\)安全校验算法流程如下图所示,校验流程如下:
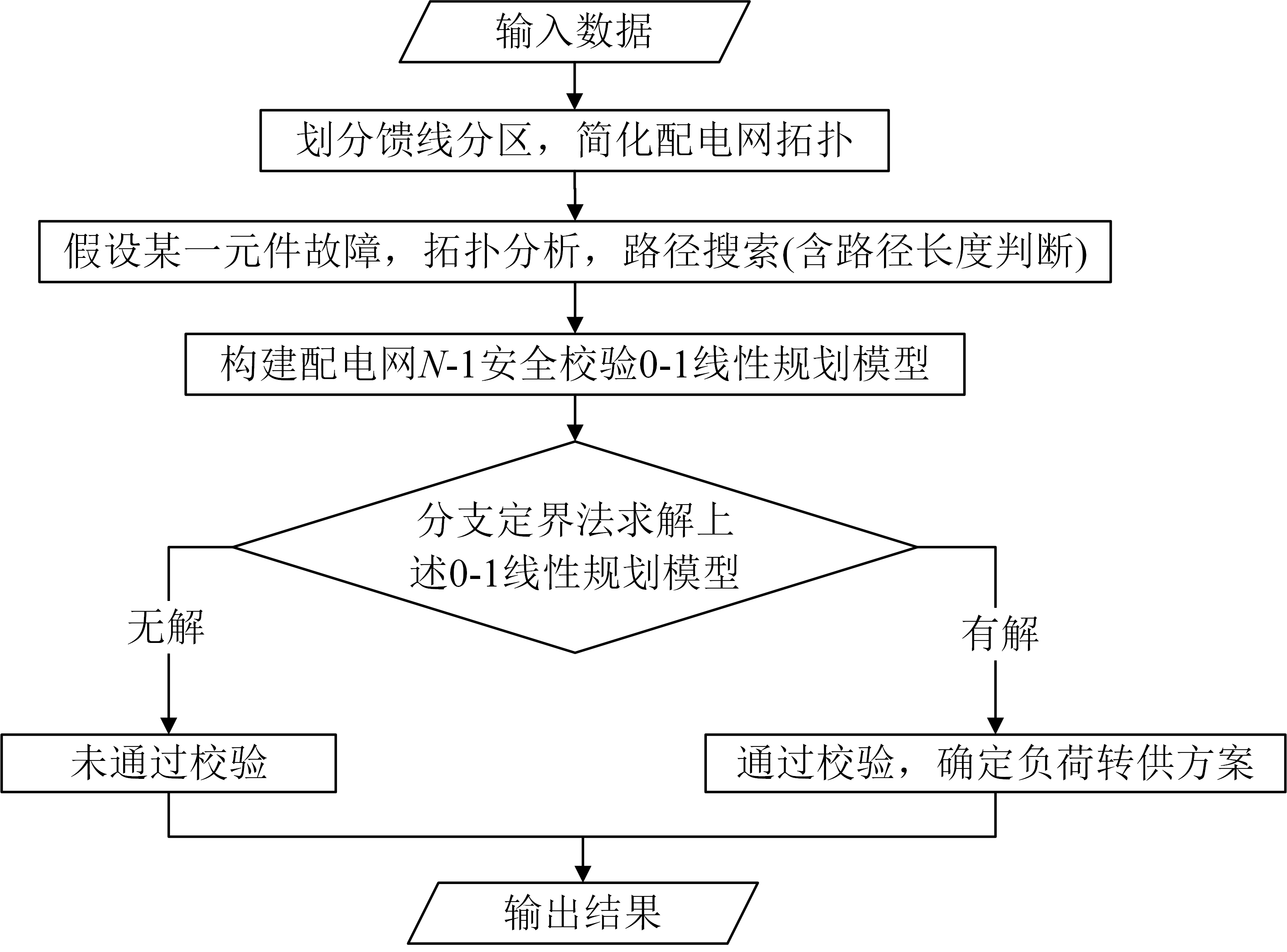
配电网N-1安全校验算例
算例网络选用某实际10 kV配电网络,如图所示。其中有5条馈线,23个馈线分区,28个动作开关装置,其中包括5个联络开关,23个分段开关。该网络馈线的容量均为19.334 MW。
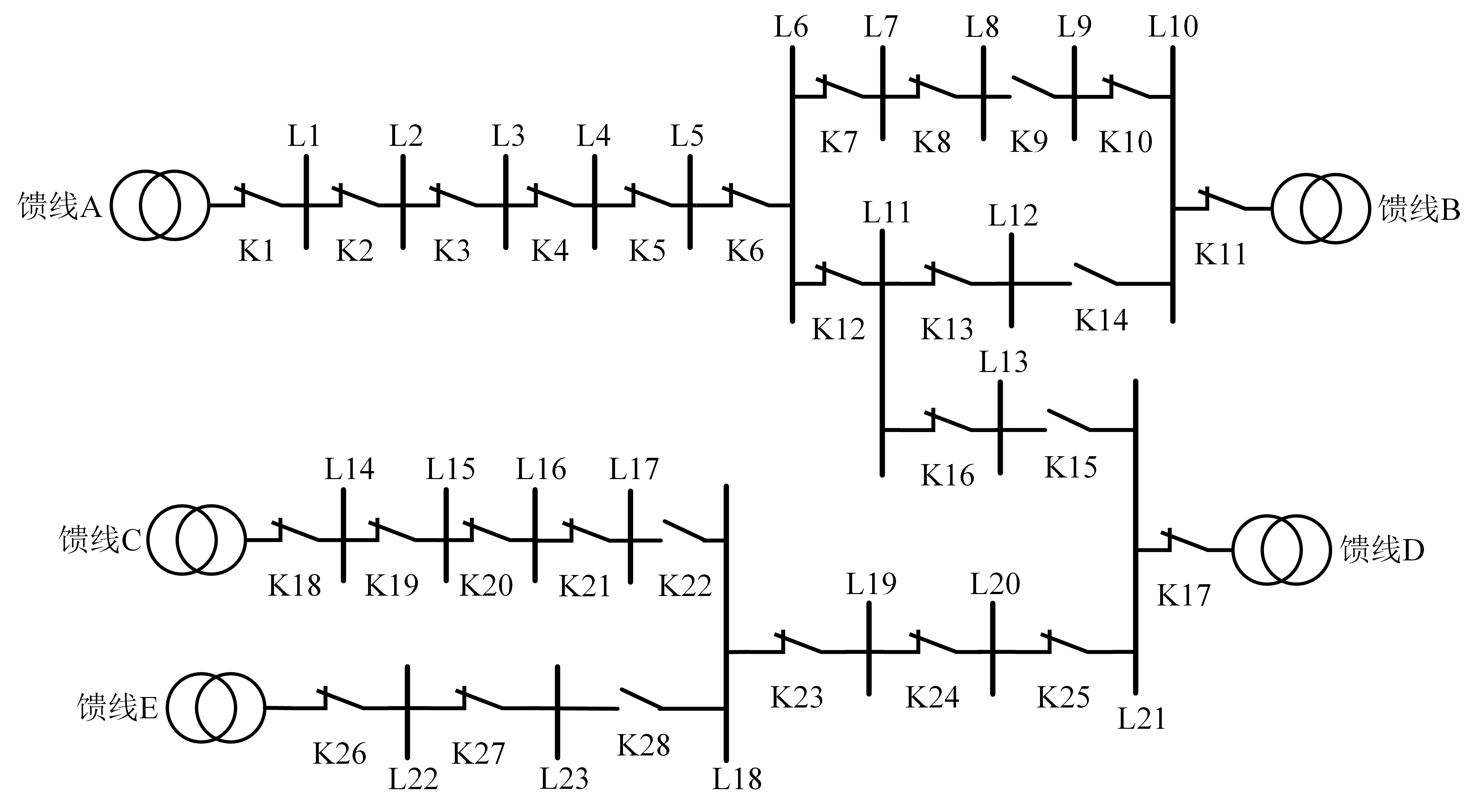
供电路径搜索
若供电路径过长,电压降较大,将导致配电网部分负荷节点电压较低,不满足供电质量要求。因此,为了保证供电质量,在路径搜索时,需计及负荷节点供电路径长度约束,根据馈线分区的供电区域类型自动剔除较长的供电路径。经搜索,算例网络共有187条供电路径。由电源节点S1~S5供电的路径分别有40、45、34、34和34条,各馈线分区供电路径数量如下表所示。
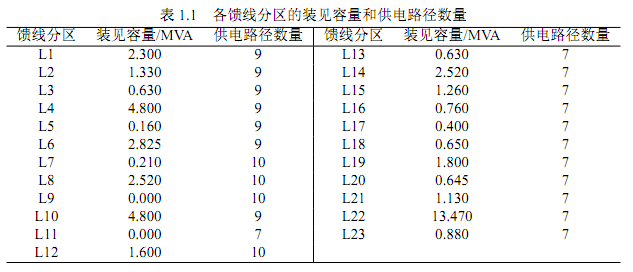
N-1安全校验
经供电路径搜索后,对算例网络进行\(N-1\)安全校验。依次架设馈线A-E出口故障,建立馈线\(N-1\)安全校验模型,利用混合整数规划软件如Cbc(Coin-or branch and cut)或Cplex等求解得到路径状态。根据模型解是否存在判断待校验馈线是否满足\(N-1\)准则,并获得负荷转供方案。算例网络的馈线\(N-1\)安全校验结果见下表。
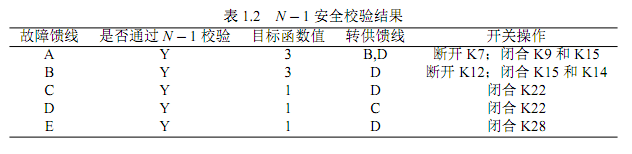
校验结果分析
校验结果显示,算例馈线组所有馈线均能通过\(N-1\)安全校验。
当馈线A故障时,待恢复供电区负载量较大,通过断开分段开关K7,可将失电区分割为两部分,分别通过馈线B和馈线D恢复供电。当馈线B故障时,馈线A负载较重,通过断开分段开关K12、闭合联络开关K15可将接入馈线A的馈线分区L11-12的负荷转移至馈线D供电,通过闭合联络开关K14即可通过馈线A转供失电区负荷。当馈线C、D和E故障时,结合图和表可知,有多种方案可实现负荷转供,基于动作开关数最少的原则,本节算法求解得到的方案仅需一个开关装置动作,操作方案较简单,大大缩短了运行人员执行操作票耗时,同时减小了误操作的可能性。
配电网供电能力分析
配电网作为电力系统中的关键一环,承担着向用户分配电能的重任。急速增长的电力需求对配电网电能质量、供电可靠性和供电能力提出了更高的要求;同时,经济的飞速发展导致建设用地紧张,获取配电网规划用地困难且投资建设成本增加。因此,充分挖掘现有配电网的供电能力具有非常重要的意义。
前面分别介绍了基于供电路径的配电网拓扑描述方法和配电网\(N-1\)安全校验方法,本节将以此为基础,构建优化模型,探讨配电网供电能力分析方法。由于在实际情况中,对于电网营销部门业扩报装工作而言,配电网供电能力以馈线可装容量对外展示。针对此情况,本节建立了面向馈线分区的\(N-1\)可装容量模型,为实际业扩报装工作提供合理有效的数据支撑。
配电网供电能力计算数学模型
本节供电能力计算分析是基于已有配电网网架和负荷分布展开的。在计算配电网供电能力、分析可消纳负荷增量时,需满足至少存在一种运行方式使配电网呈辐射状正常运行,同时该网络可通过\(N-1\)安全校验。
设负荷节点\(n_i\)可新增负荷容量为\(C_i\),则对于有\(N_\text{l}\)个负荷节点的网络,其供电能力\(TSC\)为
\[\begin{equation} TSC=\sum_{i=1}^{N_\text{l}}(L_i+C_i) \label{Eps16} \end{equation}\]将\(TSC\)最大作为目标函数,以满足馈线故障前后配电网均能长时间正常运行为约束条件建立配电网供电能力计算模型。
模型约束条件
本节计算模型的约束条件包括配电网辐射状运行约束,相应公式见上一章。此外,还有电源容量约束:
\[\begin{equation} \sum_{\pi_{i,k}\in \Pi_{S,j},\pi_{i,k}\in \Pi_{i}}W_{i,k}(L_i+C_i) \leq S_j \label{Eps17} \end{equation}\]以及馈线载流量约束:
\[\begin{equation} \sum_{\pi_{i,k}\in \Pi_{B,m},\pi_{i,k}\in \Pi_{i}}W_{i,k}(L_i+C_i) \leq F_m \label{Eps18} \end{equation}\]显然,负荷具体供电方式在不同的路径状态下可能不同,针对每个元件\(N-1\)故障的情况,通过路径搜索,得到负荷节点供电路径,分别列写约束条件,这些约束条件的集合即为待研究配电网供电能力计算模型的约束条件。
求解方法
为简化求解,引入变量:
\[\begin{equation} Z_{i,k}=W_{i,k} \cdot C_i \label{Eps19} \end{equation}\]可以证明,上述等式与下面两个不等式等价。
\[\begin{gather} |Z_{i,k}| \leq M \cdot W_{i,k} \label{Eps20}\\ |Z_{i,k}-C_i| \leq M(1-W_{i,k}) \label{Eps21} \end{gather}\]式中:\(M\)为一个足够大的常数。
设待研究配电网中共有\(\beta\)种\(N-1\)元件故障场景需要分析,则共有包括元件无故障情况在内的\(\beta+1\)种场景。综合考虑这些\(\beta+1\)种场景,可得到配电网供电能力计算的混合整数线性规划模型为
\[ \text{max}\,TSC \] \[\begin{eqnarray} \label{Eps22} \left\{\begin{aligned} &\sum_{\pi_{\alpha,i,k}\in \Pi_{\alpha,i}}W_{\alpha,i,k}=1, \quad \forall i\\ &W_{\alpha,i,k}\leq W_{\alpha,l,m}, \quad \forall \pi_{\alpha,l,m}\subset \pi_{\alpha,i,k}\\ &\sum_{\pi_{\alpha,i,k}\in \Pi_{\alpha,S,j},\pi_{\alpha,i,k}\in \Pi_{\alpha,i}}(W_{\alpha,i,k} \cdot L_i+Z_{\alpha,i,k}) \leq S_j\\ &\sum_{\pi_{\alpha,i,k}\in \Pi_{\alpha,B,m},\pi_{\alpha,i,k}\in \Pi_{\alpha,i}}(W_{\alpha,i,k} \cdot L_i+Z_{\alpha,i,k}) \leq F_m\\ &|Z_{\alpha,i,k}| \leq M \cdot W_{\alpha,i,k}\\ &|Z_{\alpha,i,k}-C_i| \leq M(1-W_{\alpha,i,k}) \end{aligned}\right. \end{eqnarray}\]式中:\(\alpha=1,2,\cdots,\beta+1\)。
面向馈线分区的N-1可装容量计算
在工程实际中,更关心的是在一个时间点上,该区域内某条馈线或者某个具体馈线分区可接入的最大容量。针对此实际需求,本节以路径状态和馈线分区可装容量为变量,构建混合整数规划模型,计算馈线分区\(N-1\)可装容量。
首先对待研究配电网络进行\(N-1\)安全校验。若不满足\(N-1\)准则,则\(N-1\)可装容量为0;若待分析配电网络可通过\(N-1\)安全校验,进而可计算满足\(N-1\)准则的馈线分区可装容量,为业扩接入方案提供数据支撑。
可装容量计算模型
设负荷节点\(l\)可接入容量为\(C_l\),将\(C_l\)最大作为目标函数,约束条件包括配电网辐射状运行约束、电源容量约束和馈线载流量约束。通过增补约束条件,将非线性模型转换为线性模型,得到各种情况下负荷节点\(l\)可装容量的混合整数线性规划模型为
\[ \text{max}\,C_l \] \[\begin{eqnarray} \label{Eps23} \left\{\begin{aligned} &\sum_{\pi_{i,k}\in \Pi_{i}}W_{i,k}=1, \quad \forall i\\ &W_{i,k}\leq W_{l,m}, \quad \forall \pi_{l,m}\subset \pi_{i,k}\\ &\sum_{\pi_{i,k}\in \Pi_{S,j},\pi_{i,k}\in \Pi_{i}}(W_{i,k} \cdot L_i+Z_{l,k}) \leq S_j\\ &\sum_{\pi_{i,k}\in \Pi_{B,m},\pi_{i,k}\in \Pi_{i}}(W_{i,k} \cdot L_i+Z_{l,k}) \leq F_m\\ &|Z_{l,k}| \leq M \cdot W_{l,k}\\ &|Z_{l,k}-C_i| \leq M(1-W_{l,k}) \end{aligned}\right. \end{eqnarray}\]通过求解上述模型,可得到负荷节点\(l\)在馈线无故障和任一条馈线出口故障时可通过\(N-1\)安全校验的可接入最大容量\(C_l\)。
可装容量计算流程
显然,负荷节点\(l\)所在馈线分区的\(N-1\)可装容量为上述各种情况下求解得到的\(C_l\)最小值。需要说明的是,由于配电网中元件众多,若针对每一元件建立模型求解供电能力和\(N-1\)可装容量,计算量很大。为简化计算,且不影响计算结果可靠性,仅考虑最严重的馈线出口故障作为元件故障情况。
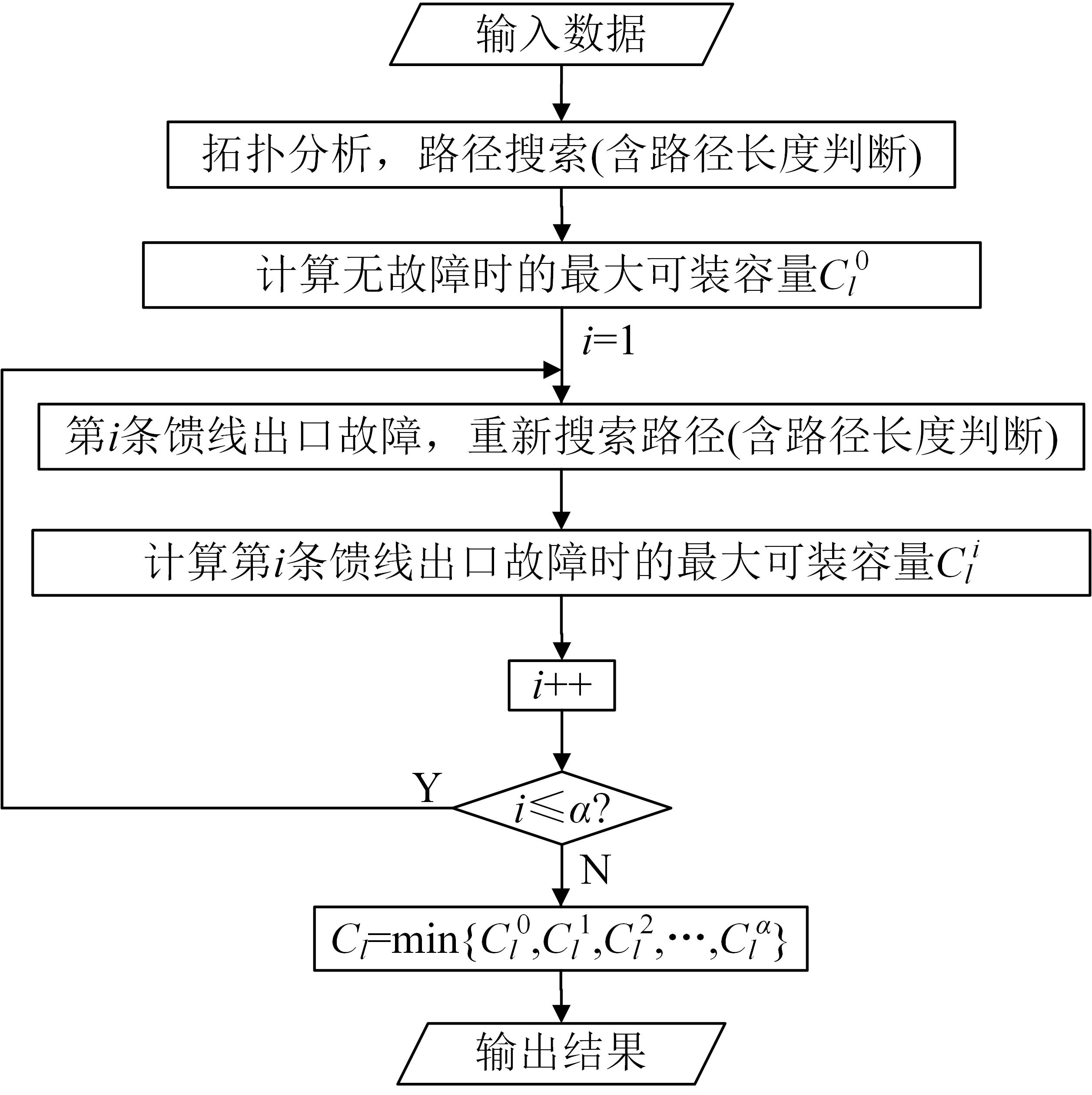
配电网供电能力分析算例
采用与上一算例相同的网络进行供电能力分析计算。根据前面所述的算法构建供电能力分析混合整数规划模型,利用开源混合整数规划软件Cbc进行求解,得到该配电网的供电能力值\(TSC=71.981\) MVA,可最大新增负荷容量为26.661 MVA,供电能力占网络电源容量的74.46%,有效地挖掘了算例网络的供电能力。在供电能力最大时各馈线分区的负荷容量分配情况如下表所示。
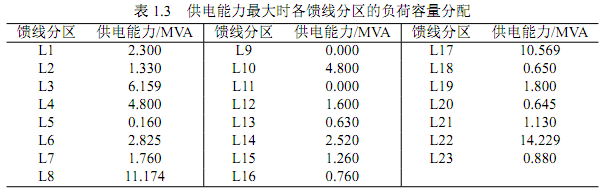
算例结果分析
在算例网络无故障,即各元件正常运行时,根据上表所示分析结果,算例网络在可接入负荷容量最大时的一种运行方式如下图所示。
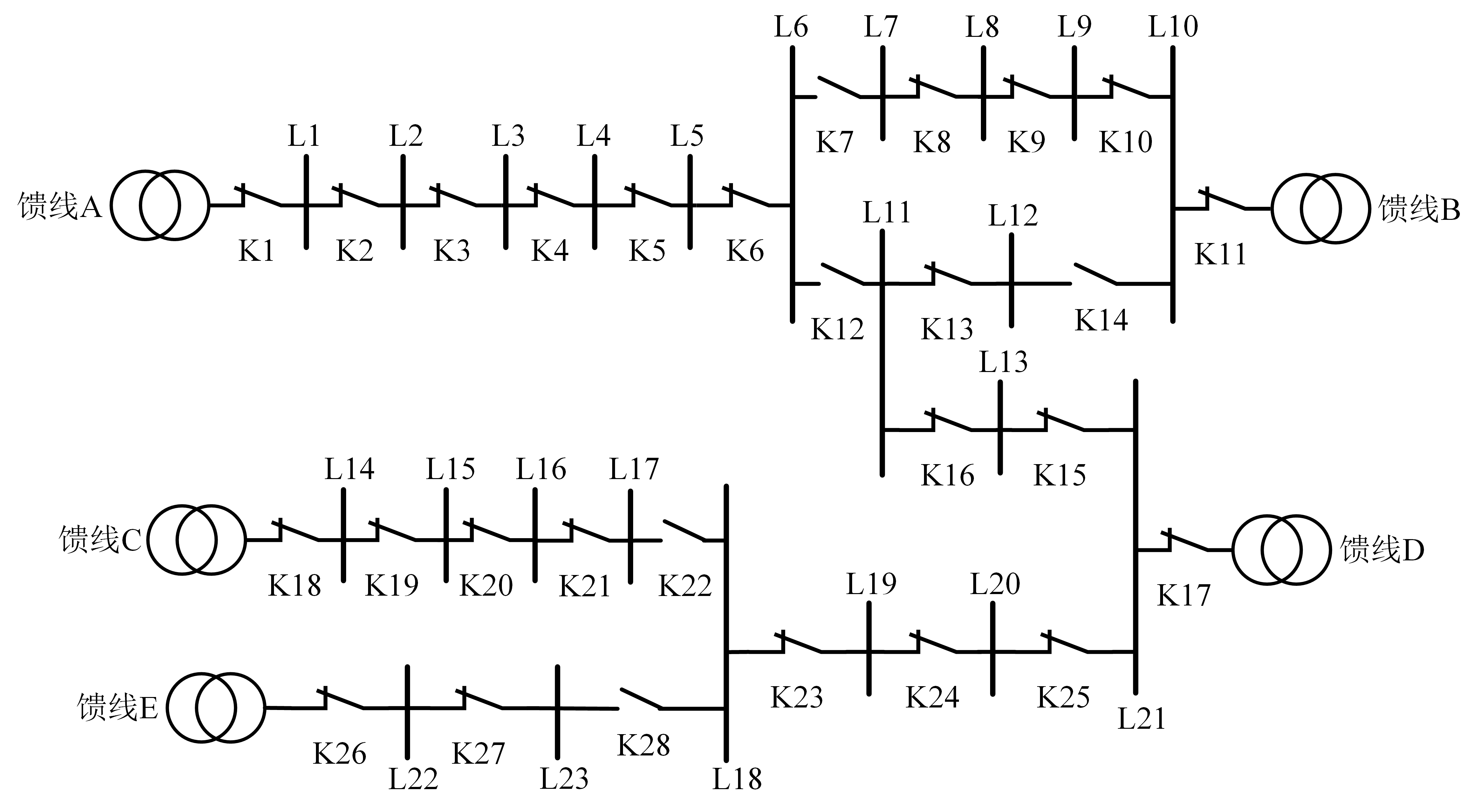
在该运行方式下,馈线A和B的负载率高达90.90%和97.72%,但馈线D的负载率仅为33.39%,选低于整体水平。经分析,这与原来的负荷分布有关,原负荷分布情况限制了供电能力的进一步提升,因此,在配电网规划阶段,合理设计负荷分布对于充分利用配电网供电能力是十分必要的。
对所介绍算法得到的配电网负荷容量分配结果进行\(N-1\)安全校验,分析计算结果的可靠性。经分析可知,在上图所示的运行方式下,网络满足\(N-1\)准则,具体校验结果见下表。

综合以上分析可知,所介绍算法可以充分挖掘网络的供电能力,计算结果可通过配电网\(N-1\)安全校验,满足配电网安全运行要求。
可装容量计算
本节利用同一网络说明可装容量计算的具体实现过程。根据馈线分区\(N-1\)可装容量计算流程,求得各馈线分区\(N-1\)可装容量计算结果如下表所示。
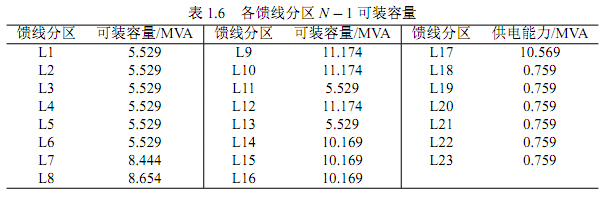
结合计算结果可知,馈线分区及与之相邻分区的装见容量和馈线联络情况均会影响\(N-1\)可装容量计算结果。例如:馈线分区L22的装见容量较大,为13.47 MVA,若其所在馈线E发生故障,则需转供的负荷量较大,考虑馈线联络和各馈线的已有负荷情况,失电区负荷仅能通过馈线D转供,故可接入馈线D和E的\(N-1\)可装容量较小。
人工评估可装容量
目前,电力局一般采用人工依据经验评估配电网馈线的可装容量。对于10kV馈线组网络,记馈线限流值为\(I_\text{per}\),馈线实际运行的最大电流值为\(I_\text{max}\),则该馈线可装容量\(C\)的计算公式为
\[\begin{equation} C=10\sqrt{3}(K \cdot I_\text{per}-I_\text{max}) \label{avlCapFormula} \end{equation}\]式中:\(K\)为经验系数,一般取0.7。
按照当前运行方式划分馈线供电的馈线分区范围,采用上式,可计算得到算例网络中各馈线的可装容量经验分析结果,例如馈线A和D的可装容量分别为4.100 MVA和6.405 MVA。对于馈线A上的各馈线分区,本节算法得到的\(N-1\)可装容量大于人工经验分析结果,馈线D的可装容量却较小。
导致该现象的原因主要是人工经验分析未充分考虑馈线联络和馈线\(N-1\)安全准则,灵活性较差。
对于馈线A,可通过馈线有效联络和分段改变该馈线组的运行方式,增大无故障时馈线A的可装容量;当馈线\(N-1\)故障时,亦可通过馈线联络与分段划分失电区负荷,恢复供电。故而,人工经验分析得到的馈线A可装容量偏小。
人工经验分析方法仅通过系数\(K\)粗略考虑馈线\(N-1\)情况,不能广泛适用于各种负荷布局和馈线联络的情况,导致馈线D可装容量计算结果过于乐观。另外,人工经验分析方法根据运行方式划分馈线供电范围,未考虑实际运行方式的变化,计算结果较为粗略。
因此,本节所介绍算法以馈线分区为单位计算\(N-1\)可装容量,较人工经验分析更为准确,计算结果更加可靠。
基于粒子群算法的配电网最大供电能力计算
配电网络重构、配电网\(N-1\)校验和供电能力分析是复杂的整数或混合整数优化问题。
近年来,随着计算机和人工智能等技术的飞速进展,一些新颖的优化算法如模拟退火算法、遗传算法和禁忌搜索算法等被用于解决配电网络重构等问题。人工智能方法的优点是能够处理问题中离散变量,但存在的缺陷是这类方法通常属于随机搜索方法,计算速度较慢。
本节介绍一种较新的智能优化算法——粒子群优化(Particle Swarm Optimization,PSO)算法,并将其用于配电网的最大供电能力的计算。
粒子群算法由来
粒子群算法是1995年由Kennedy博士和Eberhart博士提出的一种智能优化算法。该算法源于对鸟群捕食的行为研究,最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解。
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个"极值"来更新自己。第一个极值就是粒子本身所找到的最优解,这个解叫作个体极值。另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
粒子群算法计算过程
粒子群算法迭代过程中的速度更新公式如下:
\[\begin{equation} v_{id}^{t+1}=\omega v_{id}^{t}+c_1r_1(p_{id}^{t}-x_{id}^{t})+c_2r_2(p_{gd}^{t}-x_{id}^{t}) \label{Eps25} \end{equation}\]式中:\(\omega\)是惯性因子,表示粒子对当前速度有多少惯性保留,一般取0.8~1.2;\(c_1\)和\(c_2\)是学习因子,分别表示粒子对自身最优位置和对全局最优位置的学习程度,为非负实数,一般取1.5~2.0;\(r_1\)和\(r_2\)是每次迭代中的随机生成数,满足[0,1]上的均匀分布;\(D\)为粒子速度和位置的总维数;\(d\)为粒子速度和位置的维度,\(d=1,2,\cdots,D\);\(t\)为迭代次数;\(x_{id}^{t}\)为第\(t\)次迭代后,粒子\(i\)的第\(d\)维坐标;\(p_{id}^{t}\)为第\(t\)次迭代后,粒子\(i\)的历史最优位置的第\(d\)维坐标;\(p_{gd}^{t}\)为第\(t\)次迭代后,全局最优位置的第\(d\)维坐标;\(v_{id}^{t}\)为第\(t\)次迭代后,粒子\(i\)的第\(d\)维速度;粒子群规模一般取20~40。
\(v_\text{max}\)、\(v_\text{min}\)是粒子速度限值,一般由用户设定。迭代中,如果\(v_{id}^{t+1}\)>\(v_\text{max}\) ,则\(v_{id}^{t+1}\)=\(v_\text{max}\);如果 \(v_{id}^{t+1}\)<\(v_\text{min}\),则\(v_{id}^{t+1}\)=\(v_\text{max}\)。
粒子速度更新后,对各粒子坐标进行更新,坐标更新公式如下:
\[\begin{equation} x_{id}^{t+1}=x_{id}^{t}+v_{id}^{t+1} \label{Eps26} \end{equation}\]二进制粒子群算法
PSO算法最初提出是用于解决连续空间的优化问题。为解决离散空间的优化问题,Kennedy博士和Eberhart博士提出了二进制PSO算法。在二进制PSO算法中,位置的每一维分量被限制为0或1;速度的每一维分量被理解为概率,即位置的每一维分量选择0或l的概率。选择sigmiod函数将粒子的速度转换到区间[0,1]上。每次迭代粒子的速度和位置更新规则如下:
\[\begin{equation} v_{id}^{t+1}=\omega v_{id}^{t}+c_1r_1(p_{id}^{t}-x_{id}^{t})+c_2r_2(p_{gd}^{t}-x_{id}^{t}) \end{equation}\] \[\begin{equation} x_{id} =\left\{\begin{matrix} 1 & rand()<S(v_{id})\\ 0 & \text{其 他} \end{matrix}\right. \end{equation}\]式中:\(rand()\)是区间[0,l]上的随机数; \(S(v_{id})\) 是sigmoid函数,\(S(v_{id})=1/(1+exp(-v_{id}))\)。为了防止饱和,速度被限制在[-4.0,4.0]区间内。
配电网供电能力评估模型
本节的供电能力评估以负荷节点的负荷量为变量,以最大化网络的供电能力为目标,目标函数下式所示。
\[\begin{equation} \text{max}\,TSC=\sum_{i=1}^{N_l}L_i \label{Eps28} \end{equation}\]在供电能力最大化的情形下,所求得的配电网负荷分布应能使网络满足\(N-1\)准则。在\(N-1\)校验中,针对每条馈线的出口故障,均须满足下式的约束条件。
\[\begin{eqnarray} \label{Eps29} \left\{\begin{aligned} &\sum_{\pi_{i,k}\in \Pi_{i}}W_{i,k}=1, \quad \forall i\\ &W_{i,k}\leq W_{l,m}, \quad \forall \pi_{l,m}\subset \pi_{i,k}\\ &\sum_{\pi_{i,k}\in \Pi_{S,j},\pi_{i,k}\in \Pi_{i}}W_{i,k} \cdot L_i \leq S_j\\ &\sum_{\pi_{i,k}\in \Pi_{B,m},\pi_{i,k}\in \Pi_{i}}W_{i,k} \cdot L_i \leq F_m \end{aligned}\right. \end{eqnarray}\]配电网最大供电能力求解流程
设定粒子群算法中各粒子的维度为配电网负荷节点数,即每一维坐标代表一个负荷节点的负荷大小,而粒子的坐标向量代表了负荷的整体分布情况。然后用约束条件对粒子对应的负荷分布进行各类主变故障的\(N-1\)校验。若某粒子\(i\)能通过全部\(N-1\)校验,则设定该粒子的适应度值为系统所有负荷之和,即该粒子的所有坐标之和;反之,若粒子\(i\)不能通过全部的\(N-1\)校验,则应用罚函数,设定该粒子的适应度值为0。
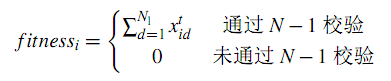
基于粒子群算法的配电网最大供电能力求解流程如下图所示。首先,读取配网信息,构建拓扑模型,然后基于深度优先原则,完成供电路径搜索。最后使用粒子群算法求解满足\(N-1\)校验的配网最大供电能力。算法输出最优粒子的坐标向量即为配电网最优负荷分布下各负荷点的负荷值,该最优粒子经过馈线出口\(N-1\)故障校验所得路径集的通断状态向量,即为对应主变故障情形下的转供方案。

粒子群算法算例
采用与之前相同的网络说明基于粒子群算法计算配电网最大供电能力的流程。在\(N-1\)约束下,当最大容量主变退出运行时,系统所有负荷均不能失电,因此该网络的最大供电能力不超过\(19.334 \times 4=77.336\) MVA。
首先通过搜索建立负荷的供电路径集,得到全系统共包含187条供电路径。然后使用粒子群算法迭代计算,设定粒子个数为20,最大迭代次数为200,算法迭代收敛过程如图所示。
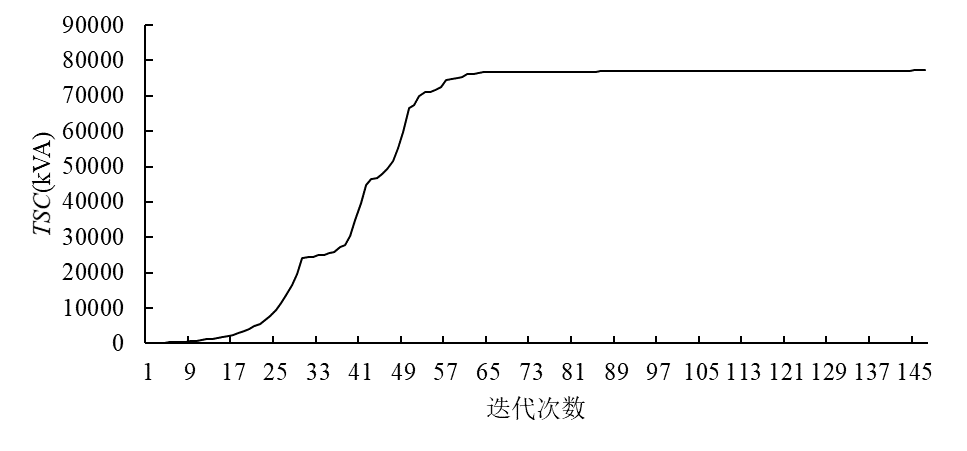
最终计算得到满足所有\(N-1\)故障情形的系统最大供电能力为77.309MVA。此时各主变负载率构成的向量为\(T_{TSC}=[99.968\%, 99.979\%, 99.919\%, 99.989\%, 0.006\%]\),各负荷的计算值大小如下表所示。
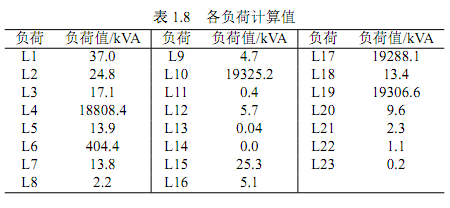
总结
上一章的配电网拓扑模型约束了配电网可行的拓扑结构,在此基础上,本章给出了更多配电网在运行中的电气量约束,用于配电网重构等实际问题的分析。
本章首先介绍了配电网重构的概念、研究现状和意义,建立了配电网网络重构的混合整数二阶锥规划模型与故障恢复控制的混合整数线性规划模型。
在此基础上,介绍了配电网\(N-1\)安全校验和配电网供电能力分析的相关概念、基于路径描述的数学模型与求解方法。配电网\(N-1\)安全校验是衡量配电网运行可靠性的重要手段,\(N-1\)准则要求配电网任意位置发生故障时,可以实现故障隔离,并结合馈线联络方式通过改变开关运行状态,转供负荷至其他馈线,满足其用电需求。
配电网的供电能力的研究、挖掘,对于提升配电网供电质量、明确配电网规划方向、推进智能电网建设具有重要的意义。
随着配电网的快速发展,用户对于用电质量的要求不断提高,考虑到电网营销数据发布需求,本章所介绍的模型和算法具有较高的实用价值和较好的应用前景。
参考文献
- 洪海峰. 含分布式电源配电网优化重构与故障恢复重构问题研究[D]. 浙江大学, 2017.
- 周湶, 解慧力, 郑柏林, 等. 基于混合算法的配电网故障重构与孤岛运行配合[J]. 电网技术, 2015, 1(1): 136-142.
- Garver L L, Van Horne P R, Wirgau K. A load supplying capability of generation transmission networks[J]. IEEE Transactions on Power Apparatus & Systems, 1979, 98(3): 957-962.
- 肖峻, 张婷, 张跃, 等. 基于最大供电能力的配电网规划理念与方法[J]. 中国电机工程学报, 2013, 33(10): 106-113.
- Xiao J, Li F, Gu W Z, et al. Total supply capability and its extended indices for distribution systems: definition, model calculation and applications[J]. IET Generation, Transmission & Distribution, 2011, 5(8): 869-876.
- Deng Y, Cai L, Ni Y. Algorithm for improving the restorability of power supply in distribution systems[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1497-1502.
- 吴文传, 张伯明, 巨云涛. 主动配电网网络分析与运行调控[M]. 北京: 科学出版社, 2016.
- Baran M E, Wu F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
- Taylor J A, Hover F S. Convex models of distribution system reconfiguration[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1407-1413.
- Farivar M, Low S H. Branch flow model: Relaxations and convexification (part I)[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
- Li N, Chen L, Low S H. Exact convex relaxation of OPF for radial networks using branch flow model[C]// IEEE Smart Grid Comm 2012 Symposium, 2012.
- Ramos E R, Exposito A G, Santos J R, et al. Path-based distribution network modeling: application to reconfiguration for loss reduction[J]. IEEE Transactions on Power Systems, 2005, 20(2): 556-564.
- 孙明, 董树锋, 夏圣峰, 等. 基于路径描述的馈线分区N-1可装容量计算方法[J]. 电力系统自动化, 2017, 41(16): 123-129.
- 孙明. 基于路径描述的配电网供电能力分析与应用[D]. 浙江大学, 2018.
- Kennedy J, Eberhart R C. Particle Swarm Optimization[C]// Proceedings of IEEE International Conference on Neural Networks, 1995.
- 朱嘉麒, 董树锋, 徐成司, 等. 考虑多次转供的配网最大供电能力评估方法[J]. 电网技术, 2019, 43(7): 2275-2281.