智能配电网络建模与分析
负荷特性与负荷模型
2020年
本次课程内容
为了达到对电力系统进行优化的目的,我们首先要研究电力系统的负荷特性,并根据负荷所消耗的功率特征进行建模。所以本节课我们将学习以下内容:
- 单个用户负荷的特性
- 配电变压器负荷的特性
- 馈线负荷的特性
- 各种负荷模型
负荷特性
什么是负荷?这个问题的答案取决于分析类型。在不同类型的分析里,对负荷的定义不尽相同。比如,在对输电系统的稳态分析(潮流研究)中和在对配电馈线二次侧设备的分析中,负荷的电气模型就不相同。电力系统中的负荷每时每刻都在变化,现实中并不存在所谓的稳态负荷。
本节课我们要研究单个用户的负荷,配电变压器负荷以及馈线负荷。
单个用户的负荷
下图描绘了单个用户的用电需求情况,展示了负荷消耗的有功功率在两个15分钟时段的变化趋势。为了更好地描述这种时刻变化的负荷,我们要先明确几个定义。
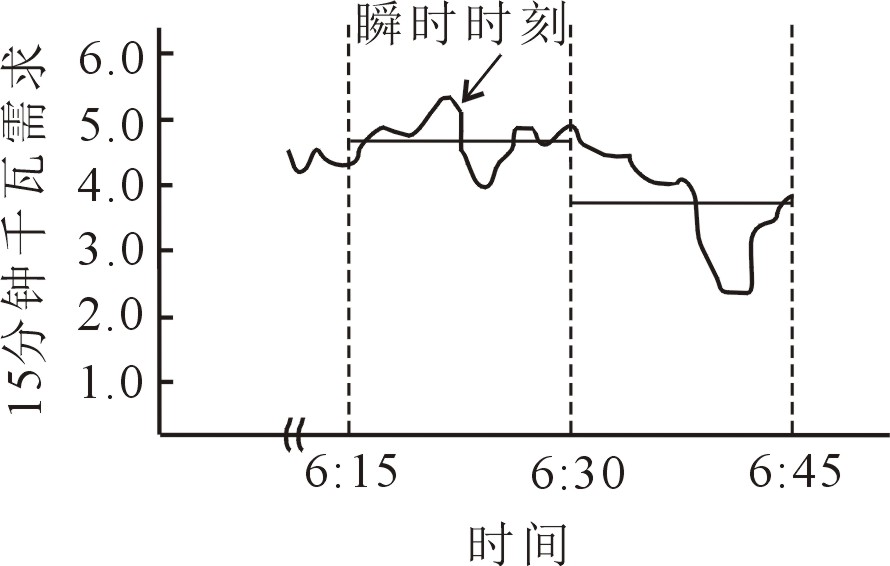
需求
一段时间内负荷消耗能量的平均值为需求。这个能量可以是有功功率、无功功率、视在功率甚至电流。在图中取15分钟为一个时间段,在每一个时间段内求出负荷消耗有功功率的平均值,然后用图中直线表示其大小,这就是15分钟有功功率需求。

最大需求
特定时间段内负荷需求的最大值为最大需求。下图是城市居民用户的典型负荷有功需求曲线,其中每个长条描述的是15分钟有功需求。若定义24小时内15分钟有功需求的最大值为15分钟最大有功需求,那么该用户24小时内15分钟最大有功需求为6.18kW,发生在13点15分。
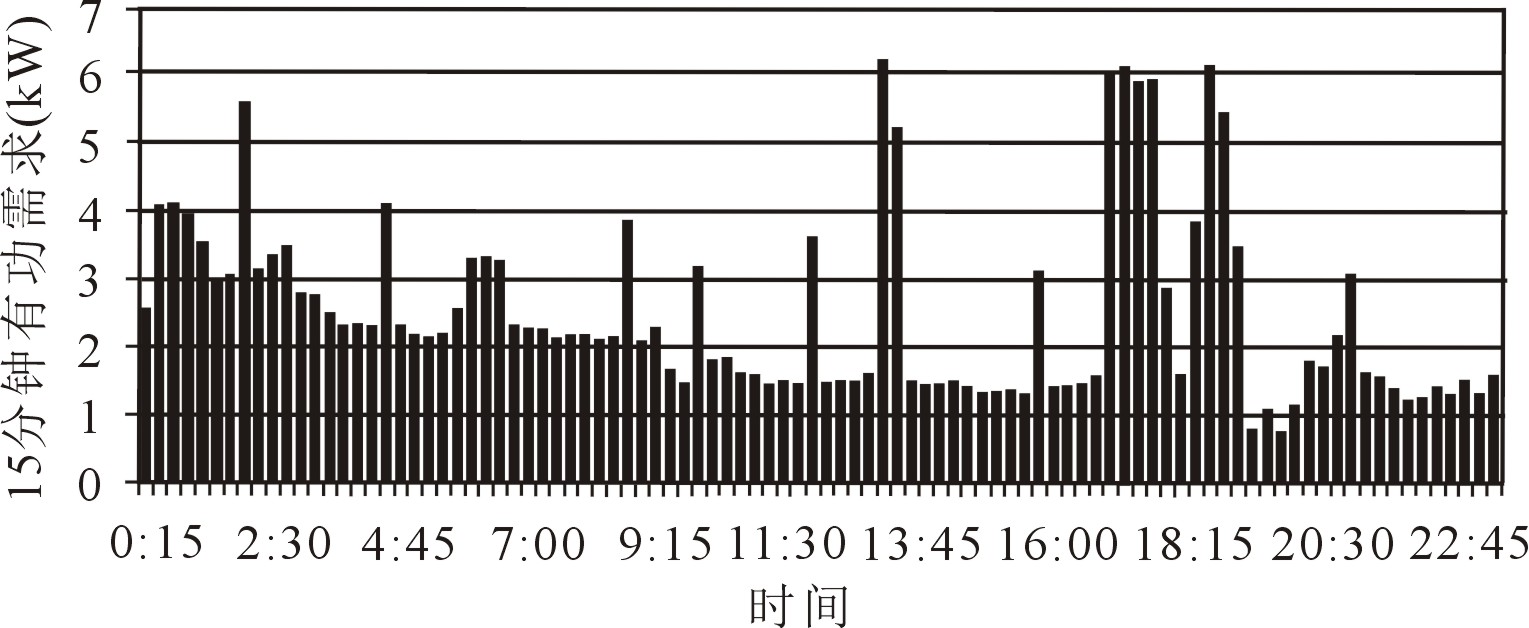
平均需求
特定时间段内负荷需求的平均值为平均需求。在每个15分钟的时间间隔内,消耗的电能计算方法如下:
\[\text{15分钟内消耗的电能}=\text{15分钟有功需求}\times \text{0.25} \text{h}\]
而一天消耗的总能量,就是每个15分钟内消耗能量的总和。从原始数据中知,用户#1在24小时内消耗的总电能为58.96kWh,因此15分钟平均有功需求计算方法如下:
\[\text{15分钟平均有功需求}=\frac{\text{总消耗电能}}{\text{小时数}}=\frac{\text{58.96}}{\text{24}}=\rm 2.46 \ (kW)\]
负荷率
特定时间段内的平均需求与最大需求之比定义为负荷率,它反映了电气设备的利用率。
对于图中的用户#1,其负荷率为
\[\text{负荷率}= \frac{\text{15分钟平均有功需求}}{\text{15分钟最大有功需求}}=\rm \frac{2.46}{6.18}=0.40\]
配电变压器负荷
一个配电变压器会给一个或多个用户供电。每个用户都会有自己的需求曲线。教材中给出了另外三个由同一配电变压器供电的用户负荷的需求曲线,它们都有自己独特的负荷特性。对于配电变压器负荷我们要明确以下几个定义:总需求、最大总需求、负荷持续时间曲线、最大非重合需求、差异系数、利用率、负荷差异程度以及需要系数。
总需求
对应单个用户负荷的需求来定义,将总需求定义为一段时间内一组负荷的需求之和。在之前描述的背景下,这四个用户的有功需求之和就是这一组负荷的总需求,也就是为它们供电的变压器的总需求。下图显示了24小时内变压器的总需求曲线。
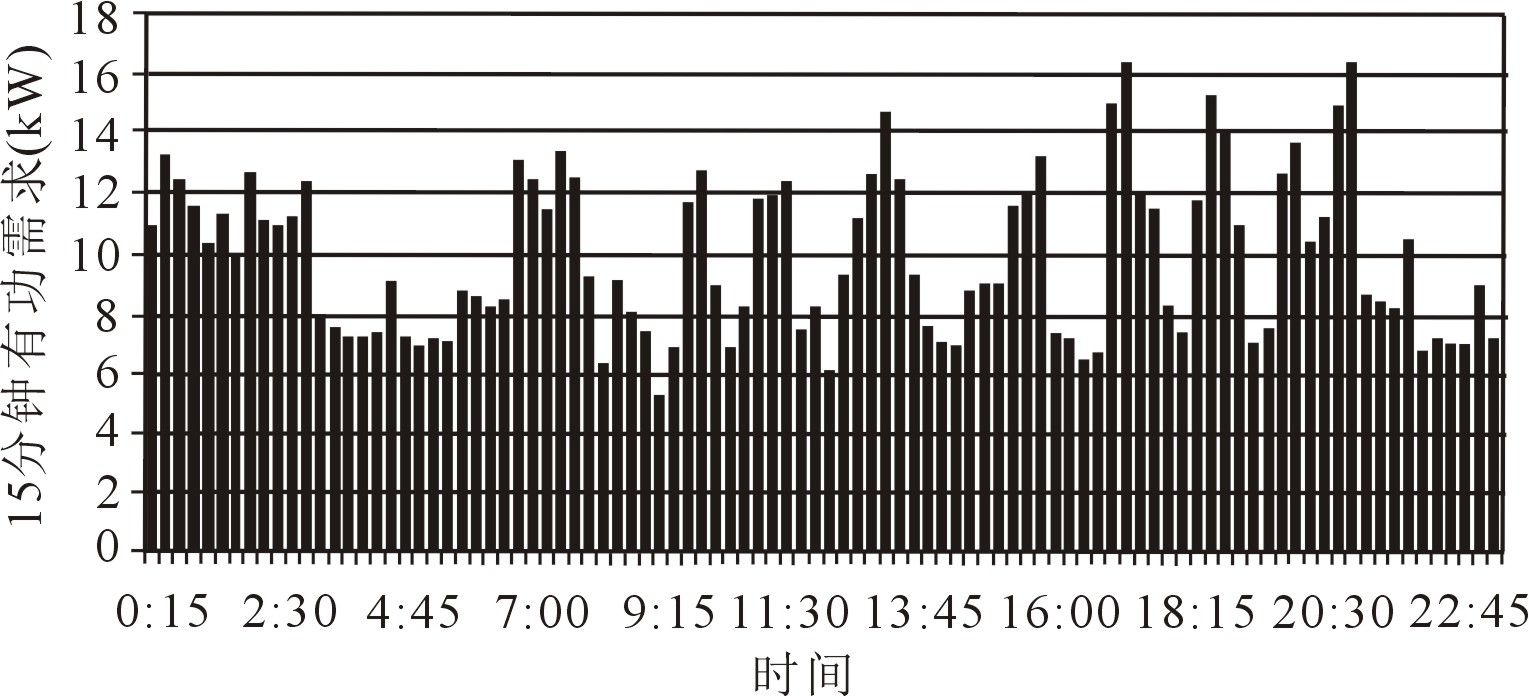
最大总需求
类似地,我们可以定义特定时间段内总需求的最大值为最大总需求。对比变压器总需求曲线和单个用户的需求曲线,可以发现多个用户负荷互相联系并组成一个整体系统时,系统外部体现出的负荷功率需求曲线会变平缓。变压器的15分钟最大总有功需求,发生在17点30分,这个时间和系统中任何单个用户最大需求出现的时间都不相同。

负荷持续时间曲线
负荷持续时间曲线是一个人为引入的定义。将变压器需求曲线按降序排序,其有功功率需求量就形成了如图所示的变压器负荷持续时间曲线。曲线横坐标是变压器在不低于某特定有功功率需求的条件下的工作时间占比,纵坐标是变压器15分钟有功需求。
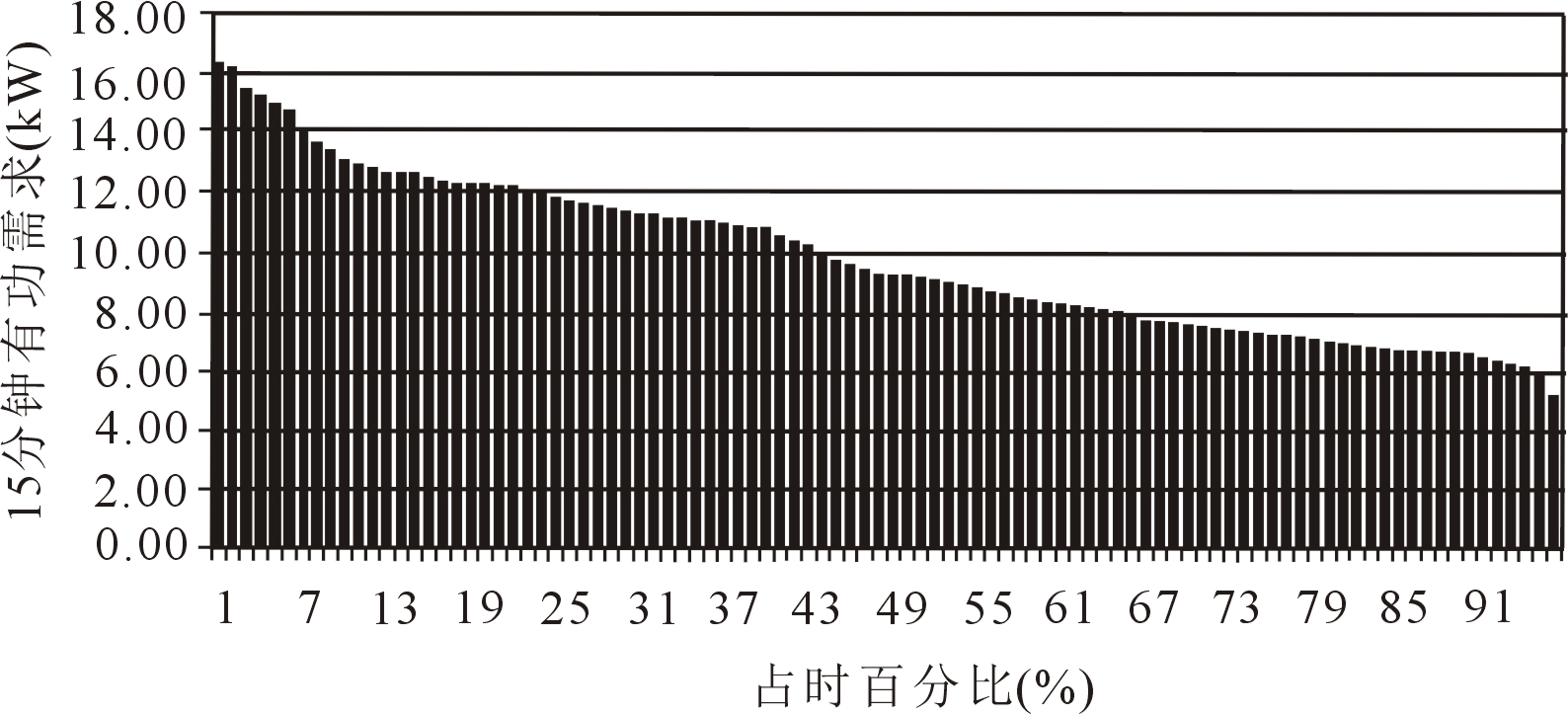
最大非重合需求
特定时间段内所有负荷的最大需求之和就是这段时间内的最大非重合需求。在上述背景下,这台配电变压器的最大非重合需求为4个用户的最大有功需求之和。
\[\text{最大非重合有功需求}=\rm 6.18+6.82+4.93+7.05=24.98\ (kW)\]
区分最大非重合需求和最大总需求的关键————是否强调同时性。最大总需求的统计要求同时性;而最大非重合需求不要求同时性,只考虑统计时间段内组内所有用户负荷需求的最大值之和。
差异系数
差异系数的定义是一组用户的最大非重合需求与最大总需求的比值,该比值一般大于1。上述背景下的配电变压器的差异系数为
\[\text{差异系数}=\frac{\text{最大非重合需求}}{\text{最大总需求}}=\rm \frac{24.98}{16.16}=1.5458\]
显然这样计算出来的差异系数只适用于这四位用户组成的群体。群体数不同,差异系数也不同。
教材中给出了一个用户数从1到70的各个群体的差异系数表。从表中看出,从70位用户起差异系数基本稳定在3.20。也就是说,用户数目较多时,可以通过计算所有用户的最大非重合需求,再除以差异系数3.20来预测最大总需求。
利用率
利用率是最大视在功率需求和变压器额定容量之比,反映了电气设备效能发挥的程度。
假设,给四个负荷供电的变压器的额定视在功率为15kVA,功率因数为0.9,15分钟最大总有功需求为16.16kW,那么该变压器的15分钟最大总视在功率需求为
\[\text{最大视在功率需求}=\frac{\text{最大有功功率需求}}{\text{功率因数}}=\rm \frac{16.16}{0.9}=17.96\ (kVA)\]
利用率为
\[\text{利用率}=\frac{\text{最大视在功率需求}}{\text{变压器额定容量}}=\rm \frac{17.96}{15}=1.197\]
负荷差异程度
负荷差异程度的定义为最大非重合需求与最大总需求的差值,显然这个值不会小于零。
对于上述我们研究的变压器,它的负荷差异程度为
\[\text{负荷差异程度}=\rm 24.97-16.16=8.81\ (kW)\]
需要系数
对于单一用户,可以定义需要系数这一概念,需要系数是用户的最大有功需求与该用户拥有的所有电气设备额定功率之和的比。
举个例子,用户#1的15分钟最大有功需求为6.18kW,假设用户#1拥有的所有电气设备的额定功率之和为35kW,那么需要系数计算如下:
\[\text{需要系数}=\frac{\text{最大有功需求}}{\text{所有电气设备额定功率之和}}=\rm \frac{6.18}{35}=0.1766\]
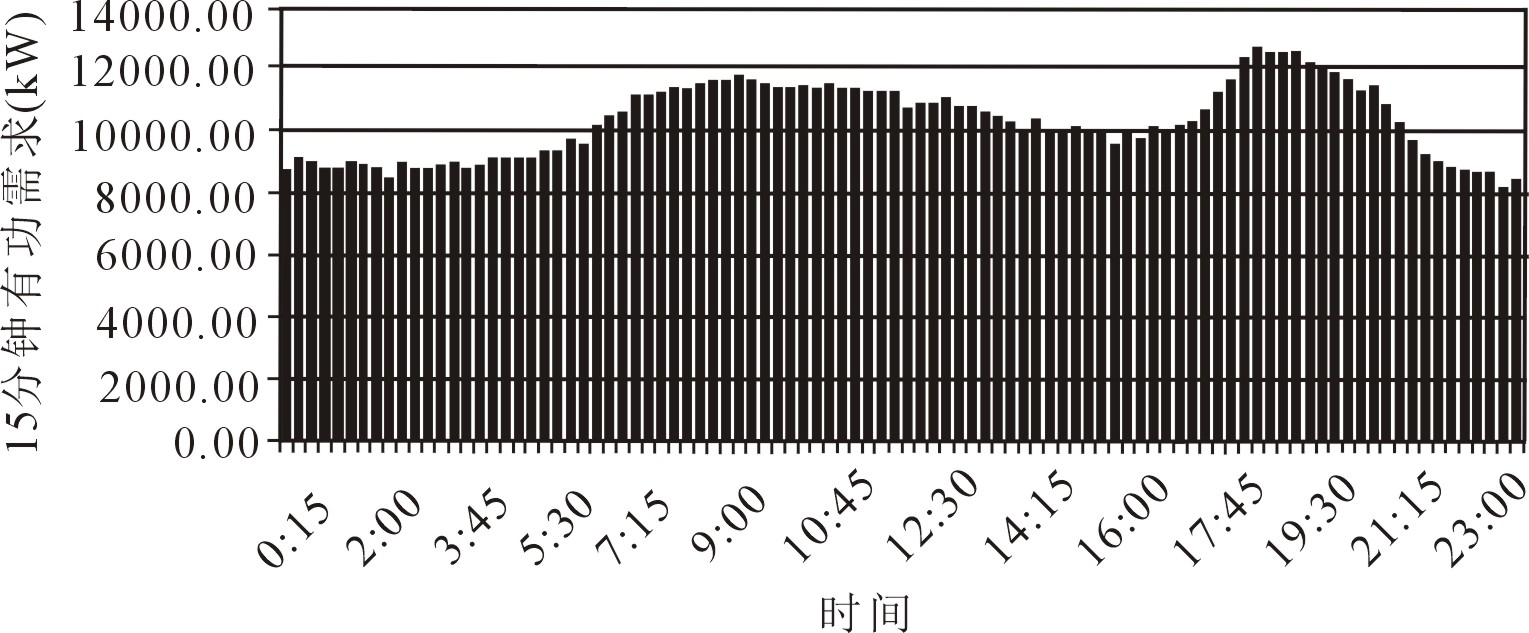
馈线负荷
如下图所示,馈线的功率需求是一条平滑的曲线,曲线上没有单个用户和变压器需求曲线上可能出现的突变现象。
最理想的馈线模型可以代表每个配电变压器,但在这之前需要确定变压器之间的负荷分配。负荷分配有以下几种方法:使用差异系数、进行负荷调查、负荷管理以及根据变压器额定容量进行分配等。
使用差异系数进行分配
按照之前的定义和说明,我们可以得到不同用户数的差异系数,然后可以确定整组用户的最大总需求,这也体现了分配到变压器上负荷的多少。
\[\text{最大总需求}=\frac{\text{最大非重合需求}}{\text{差异系数}}\]
通过负荷调查进行负荷分配
一些电力公司会对用户进行负荷调查,通过在用户处安装一个需求测量仪表,以确定消耗的电能与最大有功功率需求之间的关系。然后可以用线性回归的方法确定用户最大有功功率需求(\(P_{\text{max}}\),单位kW)与消耗电能(\(W\),单位kWh)之间的函数关系。
举个例子,下图为15位居民用户的有功功率需求与能耗函数关系示意图,经回归分析后得到的直线方程为
\[P_{\text{max}}=\text{0.1058}+\text{0.005014}\ \text{W}\]

教材给出了一个利用负荷调查的结果来分析线路负荷特性的例题5.1。
通过负荷管理进行负荷分配
变压器负荷管理程序会根据在高峰负荷月通过变压器传输的电能统计数据,确定变压器所带负荷大小。负荷管理程序主要用来确定变压器在何时因过载需要更换,也可以在进行馈线分析时用于变压器的负荷分配。
这种方法具有较高的可行性,因为电力公司在费用数据库中存有每个用户每月消耗的电能数据,如果通过已建立的数学模型明确每一个变压器供电的用户,那么在每个计费周期内,就可以确定一条馈线上各台变压器的最大总需求,完成负荷分配。
根据变压器额定容量进行负荷分配
根据变压器额定容量进行负荷分配,所需要的数据量是最少的。对于馈线来说,所有配电变压器的额定容量是已知的,因此通过仪表测量得到的视在功率需求数据,可以根据变压器的额定容量分配给每个变压器。
定义分配因数(allocation factor, AF)为测量到的三相有功功率(\(P\))或视在功率(\(S\))需求与接入电网的配电变压器额定容量之和(\(S_{\text{N}\sum}\))的比,即
\[AF=\frac{P}{S_{\text{N}\sum}} \text{或} AF=\frac{S}{S_{\text{N}\sum}}\]
每个变压器上分配的负荷大小(\(P_{\text{T}}\)或\(S_{\text{T}}\))可以按照下式计算:
\[P_{\text{T}}=AF\cdot S_{\text{N}} \text{或} S_{\text{T}}=AF\cdot S_{\text{N}} \]
举个简单的例子。如果测量得到系统的最大总有功需求是92.8kW,三个变压器的额定容量分别为25 kVA、37.5 kVA、50 kVA,要求根据变压器额定容量进行负荷分配。
变压器总额定容量:
\[\begin{gather*} S_{\text{N}\sum}=\rm 25+37.5+50=112.5\ (kV\!A)\\ AF=\rm \frac{92.8}{112.5}=0.8253\ (kW\!/kV\!A) \end{gather*}\]每台变压器分配到的有功功率为
\[\begin{gather*} \text{T1:}\ P_{\text{T1}}=\rm 0.8253\times 25=20.63\ (kW)\\ \text{T2:}\ P_{\text{T2}}=\rm 0.8253\times 37.5=30.95\ (kW)\\ \text{T3:}\ P_{\text{T3}}=\rm 0.8253\times 50=41.27\ (kW) \end{gather*}\]采用负荷分配方法计算电压降的实例
前面给出了四种负荷分配方法:使用差异系数、进行负荷调查、负荷管理和根据变压器额定容量进行分配。教材里例题5.3和5.4分别基于差异系数和变压器额定容量的负荷分配方法进行示例分析,并计算系统的电压降百分比,计算显示这两种方法得到的结果没有显著差异。
负荷模型
配电馈线上的负荷可以是星形接法或三角形接法,根据负荷特性的不同可以建模为以下几类:恒定有功功率和无功功率;恒定电流;恒定阻抗以及以上几种的组合。
下面介绍几种负荷模型,包括:星形接法负荷、三角形接法负荷、两相及单相负荷、分流电容器和三相感应电动机。这些负荷模型将用于后面的潮流计算。
星形接法负荷
下图是星形接法负荷的模型。给定\(a\)、\(b\)、\(c\)三相复功率和电压的符号如下:
\[\begin{gather} \left | S_{a} \right |\angle \theta _{a}=P_{a}+\text{j}Q_{a} \ \ \ \left | V_{an} \right |\angle \delta _{a} \label{ff1}\\ \left | S_{b} \right |\angle \theta _{b}=P_{b}+\text{j}Q_{b} \ \ \ \left | V_{bn} \right |\angle \delta _{b} \label{ff2}\\ \left | S_{c} \right |\angle \theta _{c}=P_{c}+\text{j}Q_{c} \ \ \ \left | V_{cn} \right |\angle \delta _{c} \label{ff3} \end{gather}\]
恒定有功功率和无功功率负荷(星形)
恒定有功和无功功率负荷(PQ负荷)的线电流由下式给出:
\[\begin{gather} IL_{a}=\left ( \frac{S_{a}}{V_{an}} \right )^{*}=\frac{\left | S_{a} \right |}{\left | V_{an} \right |}\angle \left ( \delta _{a}-\theta _{a} \right )=\left | IL_{a} \right |\angle \alpha _{a} \label{ff4.1}\\ IL_{b}=\left ( \frac{S_{b}}{V_{bn}} \right )^{*}=\frac{\left | S_{b} \right |}{\left | V_{bn} \right |}\angle \left ( \delta _{b}-\theta _{b} \right )=\left | IL_{b} \right |\angle \alpha _{b} \label{ff4.2}\\ IL_{c}=\left ( \frac{S_{c}}{V_{cn}} \right )^{*}=\frac{\left | S_{c} \right |}{\left | V_{cn} \right |}\angle \left ( \delta _{c}-\theta _{c} \right )=\left | IL_{c} \right |\angle \alpha _{c} \label{ff4.3} \end{gather}\]在该模型中,线到中性点电压将在每次迭代期间改变,直到其收敛。
恒定阻抗负荷(星形)
恒定阻抗负荷的阻抗值由指定的复功率和假设的线到中性点电压确定:
\[\begin{gather} Z_{a}=\frac{\left | V_{an} \right |^{2}}{S_{a}^{*}}=\frac{\left | V_{an} \right |^{2}}{S_{a}}\angle \theta _{a}=\left | Z_{a} \right |\angle \theta _{a} \label{ff5.1}\\ Z_{b}=\frac{\left | V_{bn} \right |^{2}}{S_{b}^{*}}= \frac{\left | V_{bn} \right |^{2}}{S_{b}}\angle \theta _{b} =\left | Z_{b} \right |\angle \theta _{b} \label{ff5.2}\\ Z_{c}=\frac{\left | V_{cn} \right |^{2}}{S_{c}^{*}}= \frac{\left | V_{cn} \right |^{2}}{S_{c}}\angle \theta _{c} =\left | Z_{c} \right |\angle \theta _{c} \label{ff5.3} \end{gather}\]作为恒定负荷阻抗的函数,负荷电流由下式给出:
\[\begin{gather} IL_{a}= \frac{V_{an}}{Z_{a}} =\frac{\left | V_{an} \right |} {\left | Z_{a} \right |}\angle \left ( \delta _{a}-\theta _{a} \right ) =\left | IL_{a} \right |\angle \alpha _{a} \\ IL_{b}= \frac{V_{bn}}{Z_{b}} =\frac{\left | V_{bn} \right |} {\left | Z_{b} \right |}\angle \left ( \delta _{b}-\theta _{b} \right ) =\left | IL_{b} \right |\angle \alpha _{b} \label{ff6}\\ IL_{c}= \frac{V_{cn}}{Z_{c}} =\frac{\left | V_{cn} \right |} {\left | Z_{c} \right |}\angle \left ( \delta _{c}-\theta _{c} \right ) =\left | IL_{c} \right |\angle \alpha _{c} \end{gather}\]在迭代中线到中性点电压会发生变化,但上式中计算的阻抗将保持不变。
恒定电流负荷(星形)
在该模型中,电流的大小根据恒定功率负荷下的电流计算式进行计算,然后保持恒定,同时电压的角度(\(\delta\))发生变化,导致电流角度发生变化,从而使负荷的功率因数保持恒定:
\[\begin{gather} IL_{a}=\left | IL_{a} \right |\angle \left ( \delta _{a}-\theta _{a} \right ) \\ IL_{b}=\left | IL_{b} \right |\angle \left ( \delta _{b}-\theta _{b} \right ) \label{ff7}\\ IL_{c}=\left | IL_{c} \right |\angle \left ( \delta _{c}-\theta _{c} \right ) \end{gather}\]\(\delta _{abc}\)和\(\theta _{abc}\)分别是线到中性点电压的相角和功率因数角。
组合负荷(星形)
除了上述三种单一负荷,还有组合负荷。组合负荷是由上述三种负荷模型中的每一种占总负荷的百分比来建模。
流入负荷的总线电流是三个负荷模型的总和。
教材中例题5.5给出了一个星形组合负荷的简单的潮流计算。
三角形接法负荷
三角形接法负荷的模型如下所示。 图中指定的\(ab\)相、\(bc\)相和\(ca\)相复功率和电压的符号分别如下:
\[\begin{gather} \left | S_{ab} \right |\angle \theta _{ab}=P_{ab}+\text{j}Q_{ab} \ \ \ \left | V_{ab} \right |\angle \delta _{ab} \label{ff8}\\ \left | S_{bc} \right |\angle \theta _{bc}=P_{bc}+\text{j}Q_{bc} \ \ \ \left | V_{bc} \right |\angle \delta _{bc} \label{ff9}\\ \left | S_{ca} \right |\angle \theta _{ca}=P_{ca}+\text{j}Q_{ca} \ \ \ \left | V_{ca} \right |\angle \delta _{ca} \label{ff10} \end{gather}\]
恒定有功功率和无功功率负荷(三角形)
三角形接法负荷中的电流为
\[\begin{gather} IL_{ab}=\left ( \frac{S_{ab}}{V_{ab}} \right )^{*}=\frac{\left | S_{ab} \right |}{\left | V_{ab} \right |}\angle \left ( \delta _{ab}-\theta _{ab} \right )=\left | IL_{ab} \right |\angle \alpha _{ab} \label{ff11-1}\\ IL_{bc}=\left ( \frac{S_{bc}}{V_{bc}} \right )^{*}=\frac{\left | S_{bc} \right |}{\left | V_{bc} \right |}\angle \left ( \delta _{bc}-\theta _{bc} \right )=\left | IL_{bc} \right |\angle \alpha _{bc} \label{ff11}\\ IL_{ca}=\left ( \frac{S_{ca}}{V_{ca}} \right )^{*}=\frac{\left | S_{ca} \right |}{\left | V_{ca} \right |}\angle \left ( \delta _{ca}-\theta _{ca} \right )=\left | IL_{ca} \right |\angle \alpha _{ca} \label{ff11+1}\end{gather}\]在该模型中,线电压将在每次迭代中改变,从而在每次迭代开始时产生新的电流。
恒定阻抗负荷(三角形)
恒定负荷的阻抗由指定的复功率和线电压决定:
\[\begin{gather} Z_{ab}=\frac{\left | V_{ab} \right |^{2}}{S_{ab}^{*}}= \frac{\left | V_{ab} \right |^{2}}{S_{ab}}\angle \theta _{ab}= \left | Z_{ab} \right |\angle \theta _{ab} \\ Z_{bc}=\frac{\left | V_{bc} \right |^{2}}{S_{bc}^{*}}= \frac{\left | V_{bc} \right |^{2}}{S_{bc}}\angle \theta _{bc} =\left | Z_{bc} \right |\angle \theta _{bc} \label{ff12} \end{gather}\] \[\begin{gather} Z_{ca}=\frac{\left | V_{ca} \right |^{2}}{S_{ca}^{*}}= \frac{\left | V_{ca} \right |^{2}}{S_{ca}}\angle \theta _{ca} =\left | Z_{ca} \right |\angle \theta _{ca} \end{gather}\]作为恒定负荷阻抗的函数,三角形负荷电流为:
\[\begin{gather} IL_{ab}= \frac{V_{ab}}{Z_{ab}} =\frac{\left | V_{ab} \right |} {\left | Z_{ab} \right |}\angle \left ( \delta _{ab}-\theta _{ab} \right ) =\left | IL_{ab} \right |\angle \alpha _{ab} \\ IL_{bc}= \frac{V_{bc}}{Z_{bc}} =\frac{\left | V_{bc} \right |} {\left | Z_{bc} \right |}\angle \left ( \delta _{bc}-\theta _{bc} \right ) =\left | IL_{bc} \right |\angle \alpha _{bc} \label{ff13}\\ IL_{ca}= \frac{V_{ca}}{Z_{ca}} =\frac{\left | V_{ca} \right |} {\left | Z_{ca} \right |}\angle \left ( \delta _{ca}-\theta _{ca} \right ) =\left | IL_{ca} \right |\angle \alpha _{ca} \end{gather}\]恒定电流负荷(三角形)
在该模型中,同样根据恒定功率负荷给出的公式计算电流的大小,然后保持恒定,同时在每次迭代期间电压的角度改变。这使负荷的功率因数保持不变:
\[\begin{gather} IL_{ab}=\left | IL_{ab} \right |\angle \left ( \delta _{ab}- \theta _{ab} \right ) \\ IL_{bc}=\left | IL_{bc} \right |\angle \left ( \delta _{bc}-\theta _{bc} \right ) \label{ff14}\\ IL_{ca}=\left | IL_{ca} \right |\angle \left ( \delta _{ca}-\theta _{ca} \right ) \end{gather}\]组合负荷(三角形)
和星形接法下组合负荷类似,三角形接法下的组合负荷可以由上述三种负荷模型中的每一种占总负荷的百分比来建模。
负荷的总电流是三个负荷模型的电流总和。
线电流为三角形接法负荷供电(三角形)
通过在三角形的每个节点处应用基尔霍夫电流定律来确定流入三角形接法负荷的线电流。 以矩阵形式表示,方程式为
\[\begin{eqnarray} \label{ff15} \begin{bmatrix} IL_{a}\\ IL_{b}\\ IL_{c} \end{bmatrix}=\begin{bmatrix} \text{1} & \text{0} & -\text{1}\\ -\text{1} & \text{1} & \text{0} \\ \text{0} & -\text{1} & \text{1} \end{bmatrix}\cdot \begin{bmatrix} IL_{ab}\\ IL_{bc}\\ IL_{ca} \end{bmatrix} \end{eqnarray}\]两相及单相负荷
在上述的星形和三角形接法的负荷中,可通过将缺失相的电流设置为零来为单相和两相负荷建模。对于恒定复功率、恒定阻抗和恒定电流模型,可以使用和上述类似的对应公式计算相电流。
分流电容器
分流电容器组通常用于配电系统的电压调节并提供无功功率支持。电容器组被建模为星形或三角形接法的恒定电纳。与负荷模型类似,所有电容器组都被建模为三相,对于单相和两相的情形,可将缺失相的电流设置为零。
星形接法电容器组
三相星形接法电容器组的模型如下所示。设各个相电容器单元的额定功率和额定电压单位分别为kvar和kV。每个单位的恒定电纳可以以Siemans(西门子)为单位计算。电容器单元的电纳计算如下:
\[\begin{eqnarray} \label{ff16} B_{c}=\frac{kvar}{kV_{\text{IN}}^{2}\cdot \text{1000}}\ \rm S \end{eqnarray}\]
在计算出电纳的情况下,流入电容器组提供的线电流可由下式给出:
\[\begin{gather} IC_{a}=\text{j}B_{a}\cdot V_{an}\\ IC_{b}=\text{j}B_{b}\cdot V_{bn} \label{ff17}\\ IC_{c}=\text{j}B_{c}\cdot V_{cn} \end{gather}\]三角形接法电容器组
三角形接法电容器组的模型如下所示。对于三角形接法的电容器,额定电压必须是线电压。电容器单元的电纳计算如下:
\[\begin{eqnarray} \label{ff18} B_{c}=\frac{kvar}{kV_{\text{LL}}^{2}\cdot \text{1000}}\ \rm S \end{eqnarray}\]
三角形接法电容器组(续)
在已知电纳的情况下,流入电容器组的电流由下式给出:
\[\begin{gather} IC_{ab}=\text{j}B_{a}\cdot V_{ab} \\ IC_{bc}=\text{j}B_{b}\cdot V_{bc} \label{ff19}\\ IC_{ca}=\text{j}B_{c}\cdot V_{ca} \end{gather}\]通过在每个节点处应用基尔霍夫电流定律来计算流入三角形接法电容器的线电流。 以矩阵形式表示,方程式为:
\[\begin{eqnarray} \label{ff20} \begin{bmatrix} IC_{a}\\ IC_{b}\\ IC_{c} \end{bmatrix}=\begin{bmatrix} \text{1} & \text{0} & -\text{1}\\ -\text{1} & \text{1} & \text{0} \\ \text{0} & -\text{1} & \text{1} \end{bmatrix}\cdot \begin{bmatrix} IC_{ab}\\ IC_{bc}\\ IC_{ca} \end{bmatrix} \end{eqnarray}\]三相感应电动机
在不对称电压条件下,对感应电动机的分析一般使用对称分量法,这种方法导出了电机的正序和负序等效电路。由于电机通常连接成三角形或不接地星形,所以没有零序电压和电流。
星形接法三相感应电机
星形接法三相感应电机的序等效电路如下所示,该电路在正序和负序网络都适用,区别只在负荷电阻。

其中负荷电阻\(RL\)的值按照如下定义:
\[\begin{eqnarray} \label{ff21} RL_{i}=\frac{1-s_{i}}{s_{i}}\cdot Rr_{i} \end{eqnarray}\]在正序网络中\(i\)=1,负序中\(i\)=2。
\[\begin{gather} s_{\text{1}}=\frac{n_{\text{s}}-n_{\text{r}}}{n_{\text{s}}}\left ( \text{正序} \right ) \label{ff22}\\ s_{\text{2}}=\text{2}-s_{\text{1}}\left ( \text{负序} \right ) \label{ff23}\\ n_{\text{s}}=\text{同步转速}\ \ \ n_{\text{r}}=\text{转子转速} \notag \end{gather}\]那么正序和负序网络的输入序阻抗可以确定为
\[\begin{eqnarray} \label{ff24} ZM_{i}=Rs_{i}+\text{j}Xs_{i}+\frac{\left ( \text{j}Xm_{i} \right )\left ( Rr_{i}+RL_{i}+\text{j}Xr_{i} \right )}{Rr_{i}+RL_{i}+\text{j}\left ( Xm_{i}+Xr_{i} \right )} \end{eqnarray}\]输入序导纳:
\[\begin{eqnarray} \label{ff25} YM_{i}=\frac{\text{1}}{ZM_{i}} \end{eqnarray}\]正序电机电流是
\[\begin{eqnarray} \label{ff26} IM_{i}=YM_{i}\cdot VLN_{i} \end{eqnarray}\]这类感应电动机中性点不接地,零序电流和线到中性点零序电压为零。
\[\begin{eqnarray} \label{ff27} IM_{\text{0}}=VLN_{\text{0}}=\rm 0 \end{eqnarray}\]转化为矩阵形式:
\[\begin{gather} \begin{bmatrix} IM_{\text{0}}\\ IM_{\text{1}}\\ IM_{\text{2}} \end{bmatrix}=\begin{bmatrix} \text{1} & \text{0} & \text{0} \\ \text{0} & YM_{\text{1}} & \text{0}\\ \text{0} & \text{0} & YM_{\text{2}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{\text{0}}\\ VLN_{\text{1}}\\ VLN_{\text{2}} \end{bmatrix} \label{ff28}\\ \left [ IM_{\text{012}} \right ]=\left [ YM_{\text{012}} \right ]\cdot \left [ VLN_{\text{012}} \right ] \label{ff29} \end{gather}\]在中性点不接地的情况下,唯一可以测量的电压是电机端子的线电压。在对称分量理论中,序线到中性线电压和序线电压之间的关系为:
\[\begin{eqnarray} \label{ff30} \begin{bmatrix} VLN_{\text{0}}\\ VLN_{\text{1}}\\ VLN_{\text{2}} \end{bmatrix}=\begin{bmatrix} \text{1} & \text{0} & \text{0} \\ \text{0} & t_{\text{s}}^{*} & \text{0}\\ \text{0} & \text{0} & t_{\text{s}} \end{bmatrix}\cdot \begin{bmatrix} VLL_{\text{0}}\\ VLL_{\text{1}}\\ VLL_{\text{2}} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{ff31} t_{\text{s}}=\frac{\text{1}}{\sqrt{\text{3}}}\cdot \angle{\text{30}} \end{eqnarray}\]上式可以简写为:
\[\begin{eqnarray} \label{ff32} \left [ VLN_{\text{012}} \right ]=\left [ T \right ]\cdot \left [ VLL_{\text{012}} \right ] \end{eqnarray}\]将上式代回得:
\[\begin{eqnarray} \label{ff33} \left [ IM_{\text{012}} \right ]=\left [ YM_{\text{012}} \right ]\cdot \left [ T \right ]\cdot \left [ VLL_{\text{012}} \right ] \end{eqnarray}\]上式可用于计算序线电压已知时的正序电机电流。但实际需要的是电机相电流和线电压之间的关系。对称分量理论中有:
\[\begin{gather} \left [ IM_{abc} \right ]=\left [ A_{\text{s}} \right ]\cdot \left [ IM_{\text{012}} \right ] \label{ff34}\\ \left [ VLL_{\text{012}} \right ]=\left [ A_{\text{s}} \right ]^{-1}\cdot \left [ VLL_{abc} \right ] \label{ff35} \end{gather}\]将这两式应用于上一式可以得出最终的结果:
\[\begin{eqnarray} \label{ff36} \left [ IM_{abc} \right ]=\left [ A_{\text{s}} \right ]\cdot \left [ YM_{\text{012}} \right ]\cdot \left [ T \right ]\cdot \left [ A_{\text{s}} \right ]^{-\text{1}}\cdot \left [ VLL_{abc} \right ]=\left [ YM_{abc} \right ]\cdot \left [ VLL_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{gather} \left [ YM_{abc} \right ]=\left [ A_{\text{s}} \right ]\cdot \left [ YM_{\text{012}} \right ]\cdot \left [ T \right ]\cdot \left [ A_{\text{s}} \right ]^{-\text{1}} \label{ff37}\\ \left [ YM_{abc} \right ]=\begin{bmatrix} YM_{aa} & YM_{ab} & YM_{ac}\\ YM_{ba} & YM_{bb} & YM_{bc}\\ YM_{ca}& YM_{cb} & YM_{cc} \end{bmatrix} \label{ff38} \end{gather}\]这个模型允许电动机在从启动(\(s_1=1\))到满载(\(s_1\approx 0.03\))的所有负荷情况下建模。