智能配电网络建模与分析
三相变压器模型
2020年
本次课内容
上一节我们学习了配电网电压调节和电压调节器的模型,本节我们将学习适用于辐射状配电馈线的三相变压器组的数学模型,以及戴维南等效的内容。本节要介绍的变压器连接方式主要有以下几种
三角形-接地星形
不接地星形-三角形
接地星形-接地星形
三角形-三角形
开放星形-开放三角形
预备知识
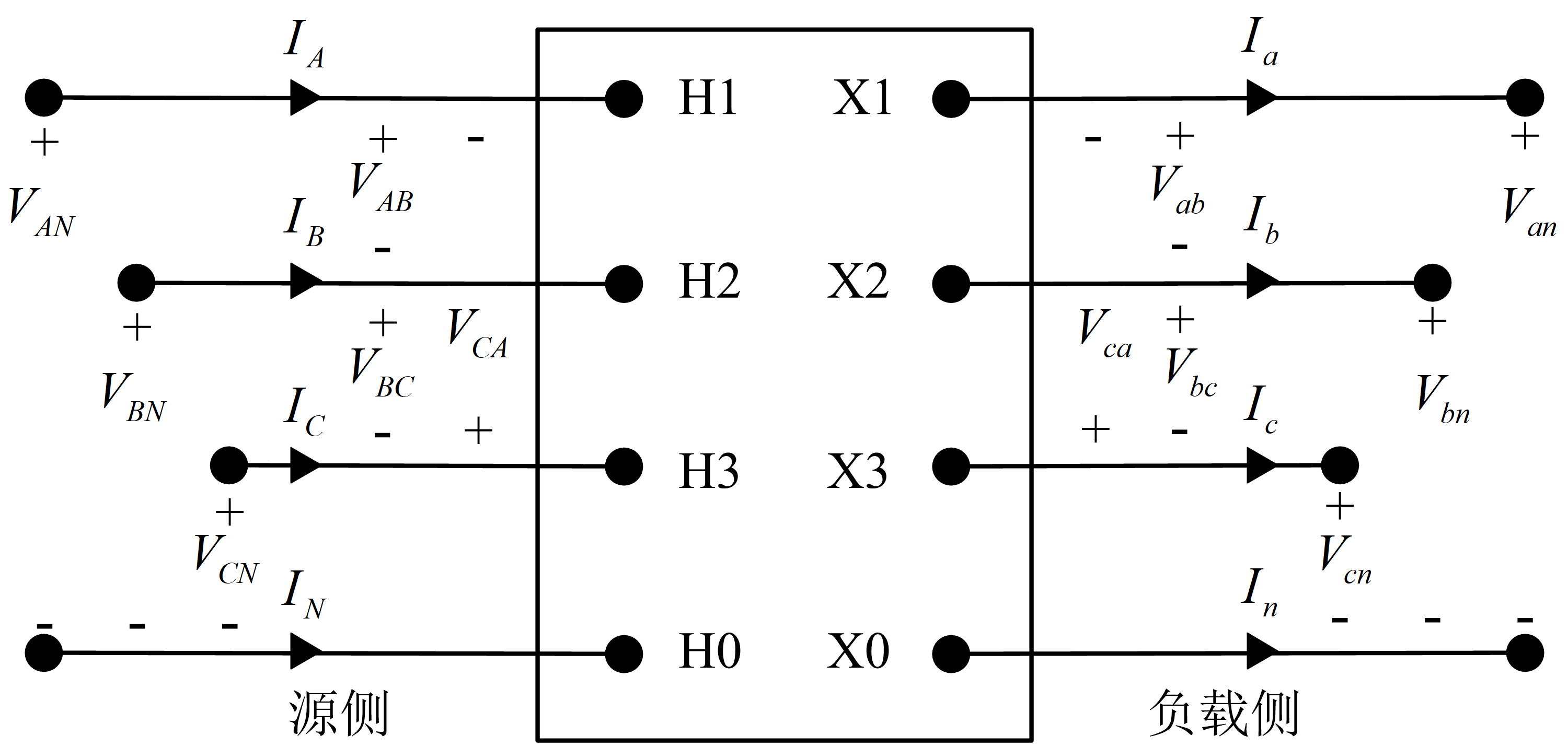
(1)三相变压器组介绍
这是一般三相变压器组示意图,它定义了连接在源端节点\(n\)和负载端节点\(m\)之间的所有变压器组的各类电压和电流。标记符号中大写字母\(A、B、C、N\)始终表示变压器组源端(节点\(n\)),小写字母\(a、b、c、n\)始终表示变压器组负载端(节点\(m\))。我们假定所有星形-三角形接法均依据国标的规定,用其所描述的相位符号可以表示正序电压和电流的标准相移为:降压接法,\(V_{AB}\)超前\(V_{ab}\) 30\(^{\circ}\),\(I_{A}\)超前\(I_{a}\) 30\(^{\circ}\);升压接法,\(V_{AB}\)滞后\(V_{ab}\) 30\(^{\circ}\),\(I_{A}\)滞后\(I_{a}\) 30\(^{\circ}\)。
预备知识(续)
(2)广义矩阵
我们按照与电压调节器模型相同的矩阵形式,推导三相变压器在不同连接方式下的模型。
节点\(n\)处的电压和电流与节点\(m\)处的电压和电流满足下式
\[\begin{gather} \left [\ VLN_{ABC} \right ] = \left [ a_{\text{t}} \right ] \cdot \left [ VLN_{abc} \right ]+\left [ b_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \label{bb1}\\ \left [ I_{ABC} \right ]= \left [ c_{\text{t}} \right ]\cdot \left [ VLN_{abc} \right ]+\left [ d_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \label{bb2} \end{gather}\]第六章将要介绍到的梯形迭代法要求节点\(m\)处的电压是节点\(n\)处的电压和节点\(m\)处的电流的函数,即
\[\begin{eqnarray} \label{bb3} \left [ VLN_{abc} \right ]= \left [ A_{\text{t}} \right ]\cdot \left [ VLN_{ABC} \right ]-\left [ B_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \end{eqnarray}\]其中,矩阵\(\left [ VLN_{ABC} \right ]\)和\(\left [ VLN_{abc} \right ]\)表示不接地星形接法变压器的线对中性点电压或者接地星形接法的线对地电压。对于三角形接法,电压矩阵表示的是等效的线对中性点电压。电流矩阵始终表示线电流。
三角形-接地星形降压接法
三角形-接地星形降压接法是一种常用的连接方式,通常用于为四线星形馈电系统供电的配电变电站。
三个单相变压器可采用标准30\(^{\circ}\)降压接法连接到三角形-接地星形连接器上。
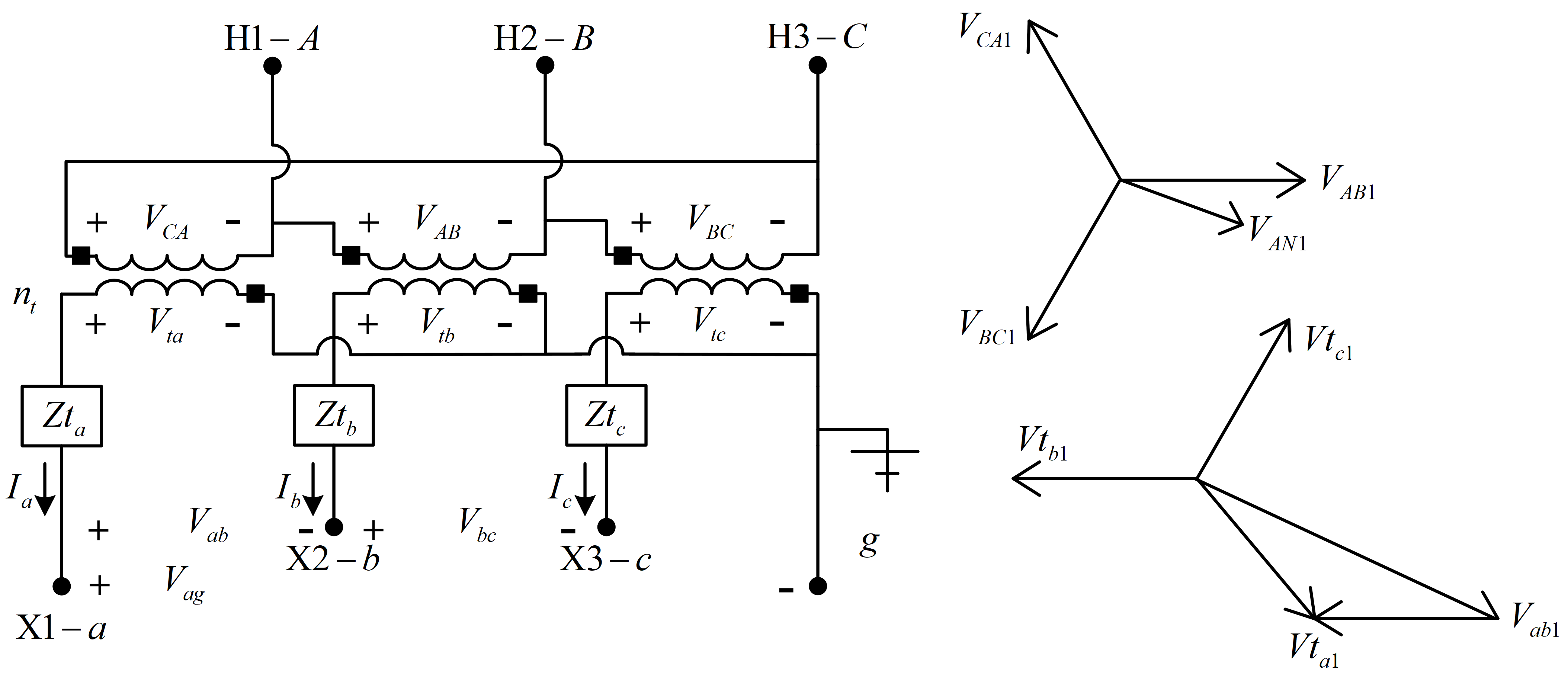
电压
上图中电压的正序相量图显示了各种正序电压之间的关系。由基尔霍夫电压定律给出的\(a\)相和\(b\)相的线电压如下
\[\begin{eqnarray} \label{bb4} V_{ab}=Vt_{a}-Vt_{b} \end{eqnarray}\]实际绕组匝数比(\(n_{\text{t}}\))定义如下
\[\begin{eqnarray} \label{bb5} n_{\text{t}}=\frac{VLL_{\text{高压侧}}}{VLN_{\text{低压侧}}} \end{eqnarray}\]则线电压相对于理想变压器电压的幅值大小为
\[\begin{eqnarray} \label{bb6} \left | VLL \right |=n_{\text{t}}\cdot \left | V_{\text{t}} \right | \end{eqnarray}\]高压侧的正序等效线对中性点电压的大小由下式给出
\[\begin{gather} \left | VLN \right |=\frac{\left | VLL \right |}{\sqrt{3}}=\frac{n_{\text{t}}}{\sqrt{3}}\cdot \left | V_{\text{t}} \right |=a_{\text{t}}\cdot \left | V_{\text{t}} \right | \label{bb7}\\ a_{\text{t}}=\frac{n_{\text{t}}}{\sqrt{3}}= \frac{VLL_{\text{高压侧}}}{\sqrt{3}\cdot VLN_{\text{低压侧}}}= \frac{VLL_{\text{高压侧}}}{VLL_{\text{低压侧}}} \label{bb8} \end{gather}\]参考变压器接法可得
\[\begin{eqnarray} \label{bb9} \begin{bmatrix} V_{AB}\\ V_{BC}\\ V_{CA} \end{bmatrix}=\begin{bmatrix} 0 & -n_{\text{t}} &0 \\ 0 & 0 &-n_{\text{t}} \\ -n_{\text{t}} & 0 &0 \end{bmatrix}\cdot \begin{bmatrix} Vt_{a}\\ Vt_{b}\\ Vt_{c} \end{bmatrix} \end{eqnarray}\]可简写为
\[\begin{eqnarray} \label{bb10} \left [ VLL_{ABC} \right ]=\left [ AV \right ]\cdot \left [ Vt_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} \left [ AV \right ]=\begin{bmatrix} 0 & -n_{\text{t}} & 0 \\ 0 & 0 & -n_{\text{t}} \\ -n_{\text{t}} & 0 & 0 \end{bmatrix} \end{eqnarray}\]这个式子表明节点\(n\)的一次侧线电压是理想二次侧电压的函数,我们需要的是节点\(n\)的等效线对中性点电压与理想二次侧电压之间的关系。
问题:如果已知线电压,怎么求等效线对中性点电压?
对称分量法
将已知线电压转化为序电压
\[\begin{eqnarray} \label{bb11} \left [ VLL_{012} \right ]=\left [ A_{\text{s}} \right ]^{-1}\cdot \left [ VLL_{ABC} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{bb12} \left [ A_{\text{s}} \right ]=\begin{bmatrix} 1 & 1 &1 \\ 1 & a_{\text{s}}^{2} &a_{\text{s}} \\ 1 & a_{\text{s}} & a_{\text{s}}^{2} \end{bmatrix} \end{eqnarray}\]\[a_{\text{s}}=1.0\angle{120}\]
正序和负序线对中性点电压和线电压之间的关系为
\[\begin{gather} \begin{bmatrix} VLN_{0}\\ VLN_{1}\\ VLN_{2} \end{bmatrix}=\begin{bmatrix} 1 & 0 &0 \\ 0 & t_{\text{s}}^{\ast } &0 \\ 0 & 0 &t_{\text{s}} \end{bmatrix}\cdot \begin{bmatrix} VLL_{0}\\ VLL_{1}\\ VLL_{2} \end{bmatrix} \label{bb13}\\ \left [ VLN_{012} \right ]=\left [ T \right ]\cdot \left [ VLL_{012} \right ] \label{bb14} \end{gather}\]其中:
\[\begin{eqnarray} \label{bb15} t_{\text{s}}= \frac{1}{\sqrt{3}}\angle{30} \end{eqnarray}\]对称分量法(续)
已知零序线电压为零,因此上式中的矩阵\([T]\)的(1,1)项可以是任意值。但为了求出等效线对中性点电压,该项值应为1.0。
等效线对中性点电压作为序电压的函数可表示为
\[\begin{eqnarray} \label{bb16} \left [ VLN_{ABC} \right ]=\left [ A_{\text{s}} \right ]\cdot \left [ VLN_{012} \right ] \end{eqnarray}\] \[\begin{eqnarray} \label{bb17} \left [ VLN_{ABC} \right ]=\left [ A_{\text{s}} \right ]\cdot \left [ T \right ]\cdot \left [ VLL_{012} \right ] \end{eqnarray}\] \[\begin{eqnarray} \label{bb18} \left [ VLN_{ABC} \right ]=\left [ W \right ]\cdot \left [ VLL_{ABC} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} [ W ]= [ A_{\text{s}} ]\cdot [ T ]\cdot [ A_{\text{s}} ]^{-1} = \frac{1}{3}\cdot \begin{bmatrix} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 1 & 0 & 2 \end{bmatrix} \end{eqnarray}\]这里提供了一种根据线电压计算等效线对中性点电压的方法。
将变压器电压关系代入上式
\[\begin{eqnarray} \label{bb19} \left [ VLN_{ABC} \right ]=\left [ W \right ]\cdot \left [ AV \right ]\cdot \left [ Vt_{abc} \right ]=\left [ a_{\text{t}} \right ]\cdot \left [ Vt_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} [ a_{\text{t}} ] = [ W ]\cdot [ AV ] = \frac{-n_{\text{t}}}{3}\cdot \begin{bmatrix} 0 & 2 & 1 \\ 1 & 0 & 2 \\ 2 & 1 & 0 \end{bmatrix} \end{eqnarray}\]理想二次侧电压是二次侧线对地电压和二次侧线电流的函数:
\[\begin{eqnarray} \label{bb20} \left [ Vt_{abc} \right ]= \left [ VLG_{abc} \right ]+\left [ Zt_{abc} \right ]\cdot \left [ I_{abc} \right ] \end{eqnarray}\]注意这里并没有限制三个变压器对应的阻抗相等。
然后结合上面两式可以得到
\[\begin{eqnarray} \label{bb22} \left [ VLN_{ABC} \right ]=\left [ a_{\text{t}} \right ]\cdot \left [ VLG_{ABC} \right ]+\left [ b_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} [ b_{\text{t}} ] = [ a_{\text{t}} ]\cdot [ Zt_{abc}]= \frac{-n_{\text{t}}}{3}\cdot \begin{bmatrix} 0 & 2\cdot Zt_{b} & Zt_{c} \\ Zt_{a} & 0 & 2\cdot Zt_{c} \\ 2\cdot Zt_{a} & Zt_{b} & 0 \end{bmatrix} \end{eqnarray}\]至此我们定义了广义矩阵\([a]\)和\([b]\)。
广义矩阵\([A]\)和\([B]\)的推导从变压器电压关系出发,理想的二次侧电压为
\[\begin{eqnarray} \label{bb24} \left [ Vt_{abc} \right ]=\left [ AV \right ]^{-1}\cdot \left [ VLL_{ABC} \right ] \end{eqnarray}\]作为等效线对中性点电压的函数,线电压表示为
\[\begin{eqnarray} \label{bb25} \left [ VLL_{ABC} \right ]= \left [ D \right ]\cdot \left [ VLN_{ABC} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{bb26} \left [ D \right ]= \begin{bmatrix} 1 & -1 & 0\\ 0& 1 & -1\\ -1& 0 & 1 \end{bmatrix} \end{eqnarray}\]结合两式有
\[\begin{eqnarray} \label{bb27} \left [ Vt_{abc} \right ]=\left [ AV \right ]^{-1}\cdot \left [ D \right ]\cdot \left [ VLN_{ABC} \right ]=\left [ A_{\text{t}} \right ]\cdot \left [ VLN_{ABC} \right ] \end{eqnarray}\]将变压器二次侧电压电流关系代入上式有
\[\begin{eqnarray} \label{bb28} \left [ VLG_{abc} \right ]+\left [ Zt_{abc} \right ]\cdot \left [ I_{abc} \right ]=\left [ A_{\text{t}} \right ]\cdot \left [ VLN_{ABC} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} [ A_{\text{t}} ] = [ AV ]^{-1}\cdot [ D ]=\frac{1}{n_{\text{t}}}\cdot \begin{bmatrix} 1 & 0 & -1 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \end{eqnarray}\]整理上式
\[\begin{eqnarray} \label{bb29} \left [ VLG_{abc} \right ]= \left [ A_{\text{t}} \right ]\cdot \left [ VLN_{ABC} \right ]-\left [ B_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{eqnarray} [ B_{\text{t}} ] = [ Zt_{abc} ] = \begin{bmatrix} Zt_{a} & 0 & 0 \\ 0 & Zt_{b} & 0 \\ 0 & 0 & Zt_{c} \end{bmatrix} \end{eqnarray}\]至此得到三角形-接地星形降压变压器接法的广义电压方程。
电流
“30\(^{\circ}\)接法”规定进入H1端子的正序电流在离开X1端子时相位滞后30\(^{\circ}\)。下图的接法和以电压表示时的接法一致,差别仅在于显示的是电流。
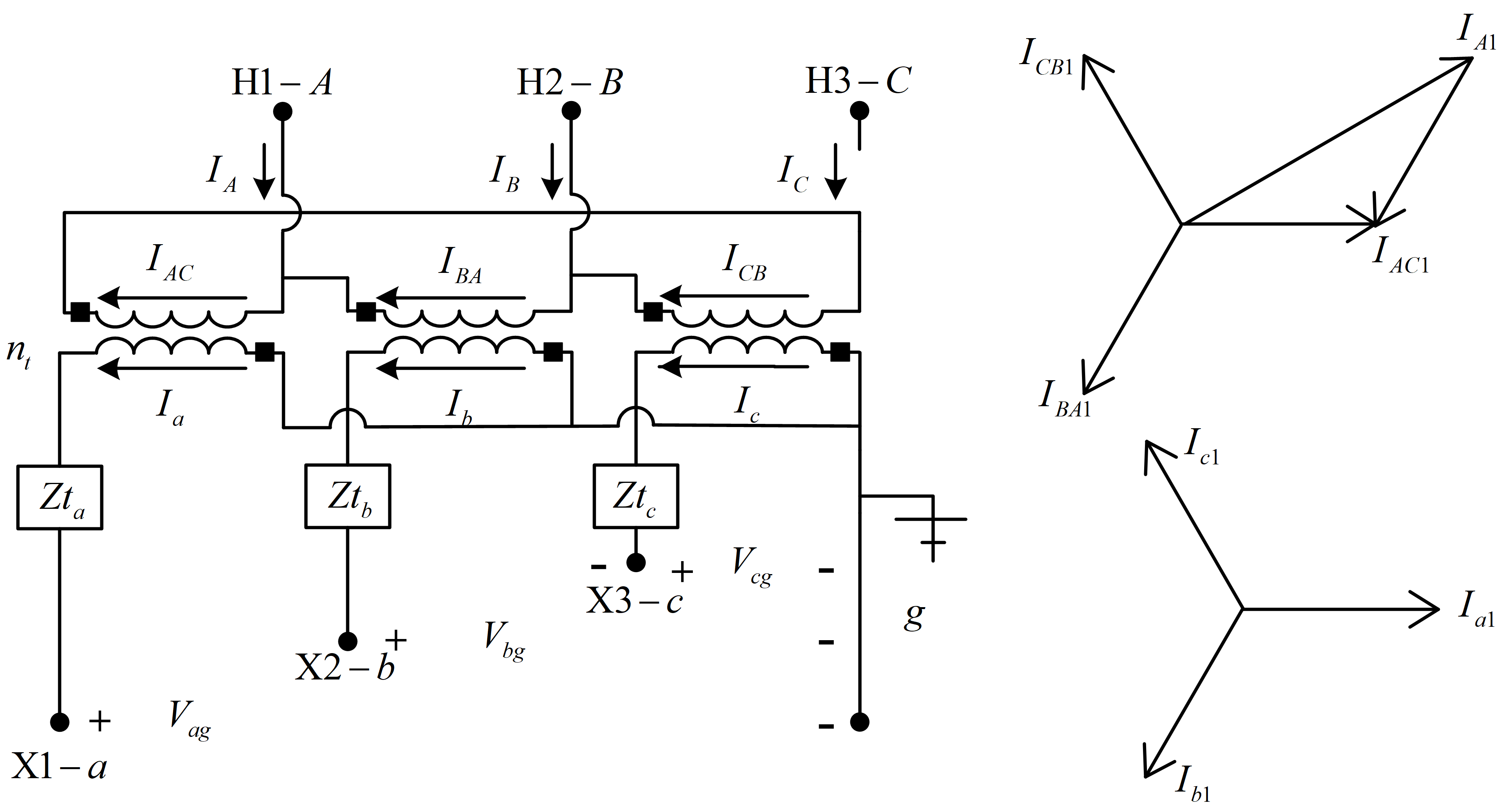
广义矩阵的推导是从变压器电流关系入手的,最后可以得到下面这个方程:
\[\begin{eqnarray} \label{bb34} \left [ I_{ABC} \right ]=\left [ D \right ]\cdot \left [ AI \right ]\cdot \left [ I_{abc} \right ] =\left [ c_{\text{t}} \right ]\cdot \left [ VLG_{abc} \right ]+\left [ d_{\text{t}} \right ]\cdot \left [ I_{abc} \right ] \end{eqnarray}\]其中:
\[\begin{gather} [ d_{\text{t}} ] = [ D ]\cdot [ AI ] = \frac{1}{n_{\text{t}}}\cdot \begin{bmatrix} 1 & -1 & 0 \\ 0 & 1 & -1 \\ -1 & 0 & 1 \end{bmatrix}\\ [ c_{\text{t}} ] = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{gather}\]说明
注意本节中推导的等式均用于降压接法。对于升压变压器,绕组之间的连接将会不同,但用于推导升压接法的广义矩阵的步骤与本节中介绍的步骤相同。
教材上这里给出一个计算并应用广义矩阵的例题4.1,这个例子还验证了一个事实————从负载到源或从源到负载计算时会得到相同的电压和电流。这个结论对之后要介绍的迭代方法来说非常重要。
不接地星形-三角形降压接法
星形-三角形接法可连接三个单相变压器,星形的中性点可以接地或不接地。常见的接法是不接地星形-三角形接法。只有不接地星形-三角形变压器接法的广义矩阵可以按照与三角形-接地星形接法相同的步骤求解。
三个单相变压器可以采用不接地星形、标准30\(^{\circ}\)接法连接,如图所示。
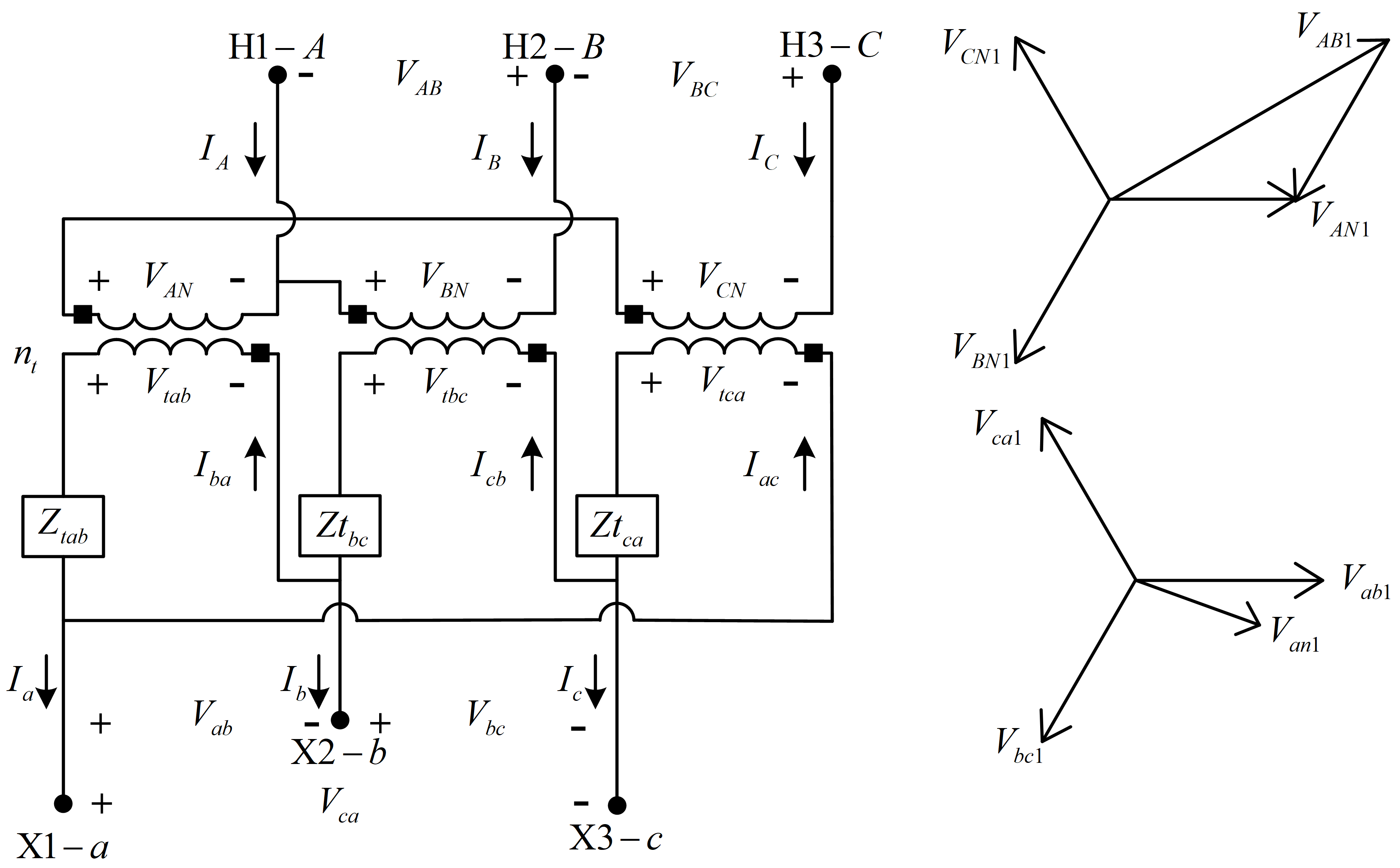
理想变压器的电压和电流与匝数比相关,可以用方程表示为
\[\begin{eqnarray} \label{bb35} \begin{bmatrix} V_{AN}\\ V_{BN}\\ V_{CN} \end{bmatrix}=\begin{bmatrix} n_{\text{t}} & 0 & 0\\ 0& n_{\text{t}} &0 \\ 0 & 0 & n_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} Vt_{ab}\\ Vt_{bc}\\ Vt_{ca} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} n_{\text{t}}= \frac{VLN_{\text{高压侧}}}{VLL_{\text{低压侧}}} \notag \\ \begin{bmatrix} VLN_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} Vt_{abc} \end{bmatrix} \label{bb36}\\ \begin{bmatrix} I_{ba}\\ I_{cb}\\ I_{ac} \end{bmatrix}= \begin{bmatrix} n_{\text{t}} & 0 &0 \\ 0& n_{\text{t}} & 0\\ 0& 0 & n_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{A}\\ I_{B}\\ I_{C} \end{bmatrix} \label{bb37}\\ \begin{bmatrix} ID_{abc} \end{bmatrix}= \begin{bmatrix} AI \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix} \label{bb38}\\ \begin{bmatrix} Vt_{abc} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}^{-1}\cdot \begin{bmatrix} VLN_{ABC} \end{bmatrix} \label{bb39} \end{gather}\]节点\(m\)处的线电压可表示为
\[\begin{gather} \begin{bmatrix} VLL_{abc} \end{bmatrix}= \begin{bmatrix} Vt_{abc} \end{bmatrix}-\begin{bmatrix} Zt_{abc} \end{bmatrix}\cdot \begin{bmatrix} ID_{abc} \end{bmatrix} \label{bb41} \end{gather}\]结合上式可得
\[\begin{eqnarray} \label{bb42} \begin{bmatrix} VLL_{abc} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}^{-1}\cdot \begin{bmatrix} VLN_{ABC} \end{bmatrix}-\begin{bmatrix} ZNt_{abc} \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} [ ZNt_{abc} ] = [ Zt_{abc} ]\cdot [ AI ]=\begin{bmatrix} n_{\text{t}}\cdot Zt_{ab} & 0 & 0 \\ 0 & n_{\text{t}}\cdot Zt_{bc} & 0 \\ 0 & 0 & n_{\text{t}}\cdot Zt_{ca} \end{bmatrix} \end{eqnarray}\]变压器组的三角形侧的线电流由下式给出
\[\begin{eqnarray} \label{bb43} \begin{bmatrix} I_{abc} \end{bmatrix}= \begin{bmatrix} DI \end{bmatrix}\cdot \begin{bmatrix} ID_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} \label{bb433} \begin{bmatrix} DI \end{bmatrix}=\begin{bmatrix} 1 & 0 &-1 \\ -1 & 1 & 0\\ 0 & -1 & 1 \end{bmatrix} \end{eqnarray}\]将变压器电流关系代入上式,有
\[\begin{eqnarray} \label{bb44} \begin{bmatrix} I_{abc} \end{bmatrix}=\begin{bmatrix} DI \end{bmatrix}\cdot \begin{bmatrix} AI \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix}= \begin{bmatrix} DY \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} [ DY ] = [ DI ]\cdot [ AI ] =\begin{bmatrix} n_{\text{t}} & 0 & -n_{\text{t}} \\ -n_{\text{t}} & n_{\text{t}} & 0 \\ 0 & -n_{\text{t}} & n_{\text{t}} \end{bmatrix} \end{eqnarray}\]因为矩阵\([DY]\)奇异,所以不能使用上式来建立一个方程式将节点\(n\)处的星形线电流与节点\(m\)处三角形线电流相关联。我们可以使用三个独立方程:三角形顶点处的两个独立的KCL方程,以及三角形的电流总和为零的等式。
\[\begin{gather} \begin{bmatrix} I_{a}\\ I_{b}\\ 0 \end{bmatrix}= \begin{bmatrix} 1 & 0 &-1 \\ -1 & 1 & 0\\ 1 & 1 & 1 \end{bmatrix}\cdot \begin{bmatrix} I_{ba}\\ I_{cb}\\ I_{ac} \end{bmatrix} \label{bb45}\\ \begin{bmatrix} I_{ba}\\ I_{cb}\\ I_{ac} \end{bmatrix}= \begin{bmatrix} 1 & 0 &-1 \\ -1& 1 &0 \\ 1 & 1 & 1 \end{bmatrix}^{-1}\cdot \begin{bmatrix} I_{a}\\ I_{b}\\ 0 \end{bmatrix}= \frac{1}{3}\cdot \begin{bmatrix} 1 & -1 & 1\\ 1& 2 &1\\ -2& -1 & 1 \end{bmatrix}\cdot \begin{bmatrix} I_{a}\\ I_{b}\\ 0 \end{bmatrix} \label{bb47}\\ \begin{bmatrix} ID_{abc} \end{bmatrix}= \begin{bmatrix} L0 \end{bmatrix}\cdot \begin{bmatrix} I_{ab0} \end{bmatrix} \label{bb48} \end{gather}\]通过将\([L0]\)矩阵的第三列设为零,可以修改上式以包含\(c\)相电流:
\[\begin{gather} \begin{bmatrix} I_{bc}\\ I_{cb}\\ I_{ac} \end{bmatrix}= \frac{1}{3}\begin{bmatrix} 1 & -1 &0 \\ 1& 2 &0 \\ -2& -1 & 0 \end{bmatrix}\cdot \begin{bmatrix} I_{a}\\ I_{b}\\ I_{c} \end{bmatrix} \label{bb49}\\ \begin{bmatrix} ID_{abc} \end{bmatrix}=\begin{bmatrix} L \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \label{bb50} \end{gather}\]求解变压器电流关系方程再代入上式
\[\begin{gather} \begin{bmatrix} I_{ABC} \end{bmatrix}= \begin{bmatrix} AI \end{bmatrix}^{-1}\cdot \begin{bmatrix} L \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \label{bb51}\\ \begin{bmatrix} d_{\text{t}} \end{bmatrix}= \begin{bmatrix} AI \end{bmatrix}^{-1}\cdot \begin{bmatrix} L \end{bmatrix}\cdot = \frac{1}{3\cdot n_{\text{t}}}\cdot \begin{bmatrix} 1 & -1 & 0\\ 1 & 2 & 0\\ -2& -1 & 0 \end{bmatrix} \label{bb52} \end{gather}\]现在引入广义矩阵\([a_{\text{t}}]\)和\([b_{\text{t}}]\)。
\[\begin{eqnarray} \label{bb53} \begin{bmatrix} VLN_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} VLL_{abc} \end{bmatrix}+\begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} ZNt_{abc} \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix} \end{eqnarray}\]\[\begin{bmatrix} VLN_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} VLL_{abc} \end{bmatrix}+ \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} ZNt_{abc} \end{bmatrix}\cdot \begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix}\]
而
\[\begin{eqnarray} [ VLL_{abc} ] = [ D ]\cdot [ VLN_{abc} ]\end{eqnarray}\]因此我们可以得到
\[\begin{bmatrix} VLN_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot\begin{bmatrix} D \end{bmatrix} \cdot \begin{bmatrix} VLN_{abc} \end{bmatrix}+\begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} ZNt_{abc} \end{bmatrix}\cdot \begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix}\] \[\begin{eqnarray} \label{bb54} \begin{bmatrix} VLN_{ABC} \end{bmatrix}=\begin{bmatrix} a_{\text{t}} \end{bmatrix}\cdot\begin{bmatrix} VLN_{abc} \end{bmatrix}+\begin{bmatrix} b_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} [a_{\text{t}}] = [AV] \cdot [D] = n_{\text{t}} \cdot \begin{bmatrix} 1 & -1 & 0 \\ 0 & 1 & -1 \\ -1 & 0 & 1 \end{bmatrix} \\ [b_{\text{t}}] = [AV] \cdot [ZNt_{abc}] \cdot [d_{\text{t}}] = \frac{n_{\text{t}}}{3} \cdot \begin{bmatrix} Zt_{ab} & -Zt_{ab} & 0 \\ Zt_{bc} & 2 \cdot Zt_{bc} & 0 \\ -2 \cdot Zt_{ca} & -Zt_{ca} & 0 \end{bmatrix} \end{gather}\]为计算从负载到源的电压和电流,这里建立了广义常数矩阵。
使用之前得到的线电压和等效线对中性点电压之间的关系:
\[\begin{eqnarray} \label{bb56} \begin{bmatrix} VLN_{abc} \end{bmatrix}= \begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} VLL_{abc} \end{bmatrix} \end{eqnarray}\]则上式可变为:
\[\begin{eqnarray} \label{bb57} \begin{bmatrix} VLN_{abc} \end{bmatrix}= \begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{ABC} \end{bmatrix}-\begin{bmatrix} B_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} [A_{\text{t}}] = [W]\cdot [AV]^{-1} = \frac{1}{3\cdot n_{\text{t}}} \cdot \begin{bmatrix} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 1 & 0 & 2 \end{bmatrix} \\ [B_{\text{t}}] = [W]\cdot [ZNt_{abc}]\cdot [d_{\text{t}}] =\frac{1}{9} \cdot \begin{bmatrix} 2\cdot Zt_{ab}+Zt_{bc} & 2\cdot Zt_{bc}-2\cdot Zt_{ab} & 0 \\ 2\cdot Zt_{bc}-2\cdot Zt_{ca} & 4\cdot Zt_{bc}-Zt_{ca} & 0 \\ Zt_{ab}-4\cdot Zt_{ca} & -Zt_{ab}-2\cdot Zt_{ca} & 0 \end{bmatrix} \end{gather}\]至此我们就针对不接地星形-三角形变压器接法建立了广义矩阵。
接地星形-接地星形接法
接地星形-接地星形接法主要用于在四线多接地系统中为单相和三相负载供电,其接法如下图所示。
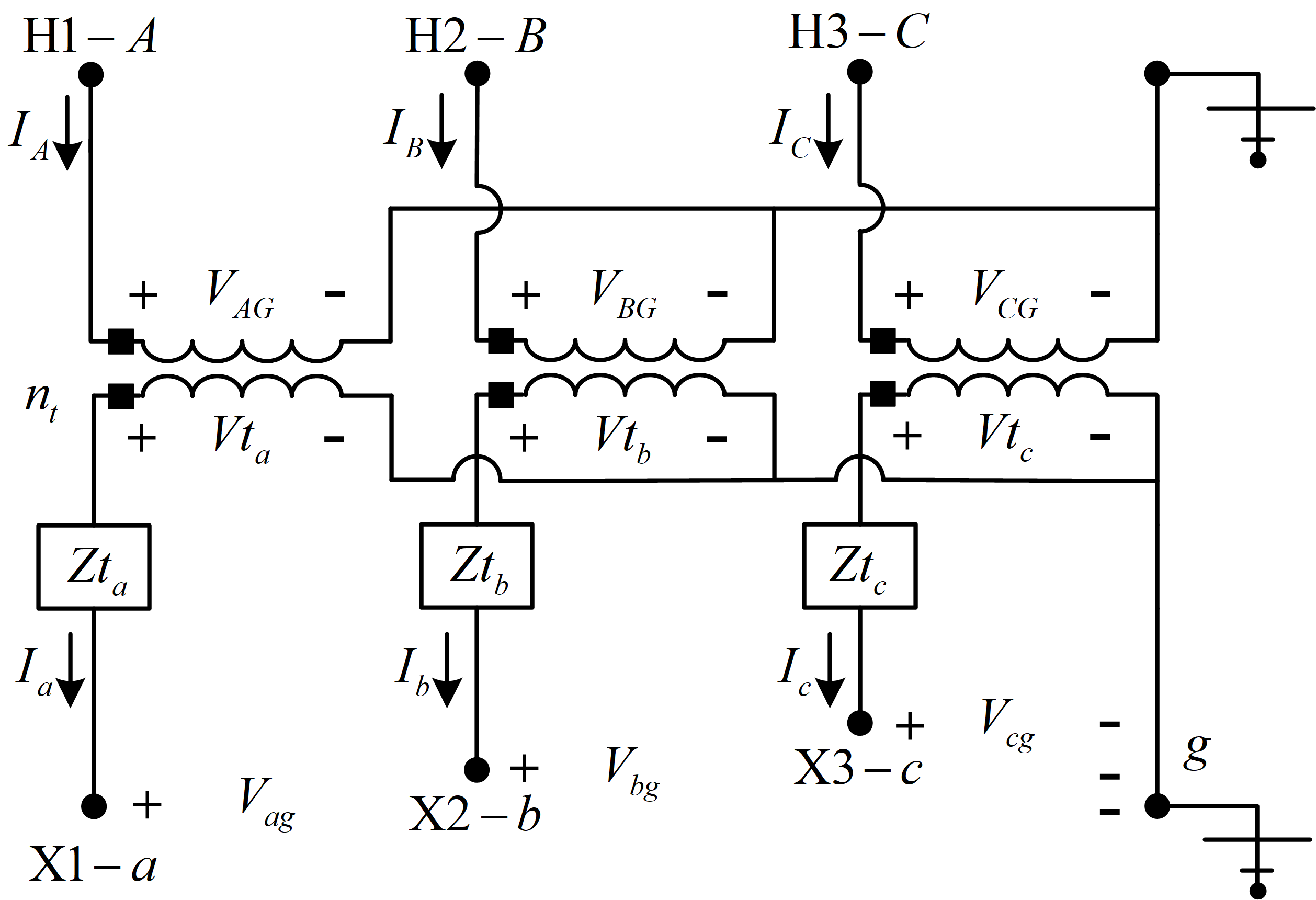
参照上图,二次侧绕组上的理想变压器电压可以通过下式计算
\[\begin{gather} \begin{bmatrix} Vt_{a}\\ Vt_{b}\\ Vt_{c} \end{bmatrix}= \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}+\begin{bmatrix} Zt_{a} & 0 & 0\\ 0 & Zt_{b} &0 \\ 0& 0 & Zt_{c} \end{bmatrix}\cdot \begin{bmatrix} I_{a}\\ I_{b}\\ I_{c} \end{bmatrix} \label{bb58}\\ \begin{bmatrix} Vt_{abc} \end{bmatrix}= \begin{bmatrix} VLG_{abc} \end{bmatrix}+\begin{bmatrix} Zt_{abc} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \label{bb59} \end{gather}\]一次侧的线对地电压通过匝数比与理想的变压器电压相关联。
\[\begin{gather} \begin{bmatrix} V_{AG}\\ V_{BG}\\ V_{CG} \end{bmatrix}= \begin{bmatrix} n_{\text{t}} & 0 &0 \\ 0& n_{\text{t}} &0 \\ 0 & 0& n_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} Vt_{a}\\ Vt_{b}\\ Vt_{c} \end{bmatrix} \label{bb60}\\ \begin{bmatrix} VLG_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} Vt_{abc} \end{bmatrix} \label{bb61} \end{gather}\]结合两式有
\[\begin{eqnarray} \label{bb62} \begin{bmatrix} VLG_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} VLG_{abc} \end{bmatrix}+\begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} Zt_{abc} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]该式为广义形式,其中矩阵\([a]\)的\([b]\)定义如下:
\[\begin{gather} \begin{bmatrix} a_{\text{t}} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}= \begin{bmatrix} n_{\text{t}} & 0 & 0\\ 0& n_{\text{t}} & 0\\ 0 & 0 & n_{\text{t}} \end{bmatrix} \label{bb63}\\ \begin{bmatrix} b_{\text{t}} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} Zt_{abc} \end{bmatrix}=\begin{bmatrix} n_{\text{t}}\cdot Zt_{a} & 0 & 0\\ 0& n_{\text{t}}\cdot Zt_{b} & 0\\ 0&0 & n_{\text{t}}\cdot Zt_{c} \end{bmatrix} \label{bb64} \end{gather}\]一次侧线电流由下式给出
\[\begin{gather} \begin{bmatrix} I_{ABC} \end{bmatrix}= \begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \label{bb65}\\ \begin{bmatrix} d_{\text{t}} \end{bmatrix}= \begin{bmatrix} \frac{1}{n_{\text{t}}} & 0 &0 \\ 0& \frac{1}{n_{\text{t}}} &0 \\ 0 & 0 & \frac{1}{n_{\text{t}}} \end{bmatrix} \label{bb66} \end{gather}\]对于二次侧线对地电压,求解之前的广义电压方程可以得到它的逆等式
\[\begin{eqnarray} \label{bb67} \begin{bmatrix} VLG_{abc} \end{bmatrix}=\begin{bmatrix} AV \end{bmatrix}^{-1}\cdot \begin{bmatrix} VLG_{ABC} \end{bmatrix}-\begin{bmatrix} Zt_{abc} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} [ A_{\text{t}} ] = [ AV ]^{-1} \end{eqnarray}\] \[\begin{eqnarray} [ B_{\text{t}} ] = [ Zt_{abc} ] \end{eqnarray}\]这样我们也可以得到逆等式常数矩阵。
三角形-三角形接法
三角形-三角形接法主要用于三线三角形系统,为三相负载或三相和单相负载的组合供电。下图显示了三个单相变压器的三角形-三角形接法。
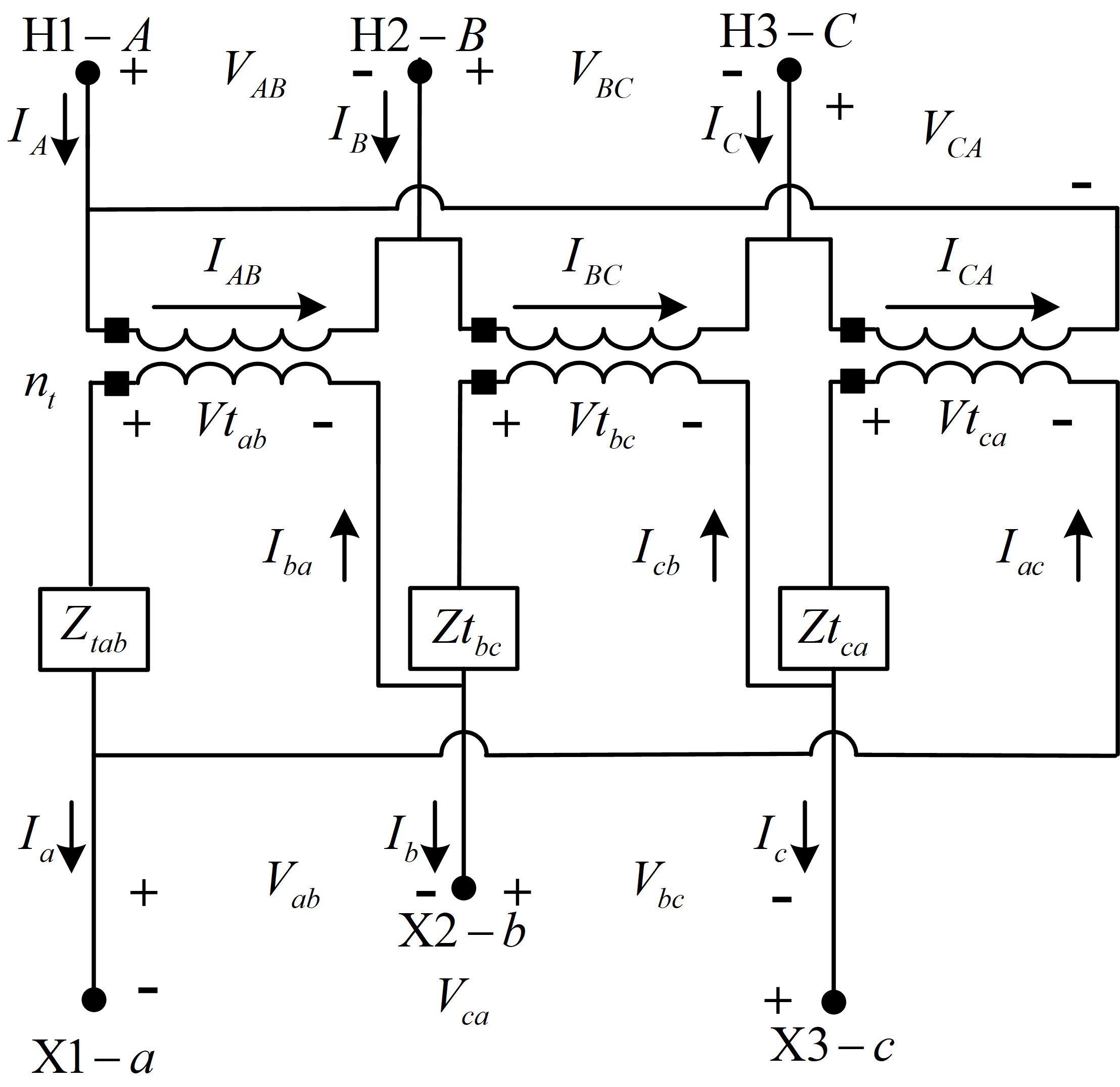
类似地我们还是从基本理想变压器电压和电流方程入手,最后可以推导得到广义方程。
基本理想变压器的电压和电流方程如下
\[\begin{gather} \begin{bmatrix} VLL_{AB}\\ VLL_{BC}\\ VLL_{CA} \end{bmatrix}= \begin{bmatrix} n_{\text{t}} & 0 &0 \\ 0& n_{\text{t}} & 0\\ 0& 0 & n_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} Vt_{ab}\\ Vt_{bc}\\ Vt_{ca} \end{bmatrix} \label{bb70}\\ \begin{bmatrix} VLL_{ABC} \end{bmatrix}= \begin{bmatrix} AV \end{bmatrix}\cdot \begin{bmatrix} Vt_{abc} \end{bmatrix} \label{bb71}\\ \begin{bmatrix} I_{ba}\\ I_{cb}\\ I_{ac} \end{bmatrix}= \begin{bmatrix} n_{\text{t}} &0 &0 \\ 0& n_{\text{t}} &0 \\ 0 & 0 & n_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{AB}\\ I_{BC}\\ I_{CA} \end{bmatrix} \label{bb72}\\ \begin{bmatrix} ID_{abc} \end{bmatrix}= \begin{bmatrix} AI \end{bmatrix}\cdot \begin{bmatrix} ID_{ABC} \end{bmatrix} \label{bb73} \end{gather}\]其中:
\[\begin{eqnarray} \label{bb74} n_{\text{t}}= \frac{VLL_{\text{高压侧}}}{VLL_{\text{低压侧}}} \end{eqnarray}\]最后我们可以得到的如下的广义方程
广义电压方程:
\[\begin{eqnarray} \label{bb97} \begin{bmatrix} VLN_{ABC} \end{bmatrix}=\begin{bmatrix} a_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{abc} \end{bmatrix}+\begin{bmatrix} b_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} [a_{\text{t}}] = [W]\cdot [AV]\cdot [D] = \frac{n_{\text{t}}}{3} \cdot \begin{bmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{bmatrix} \\ [b_{\text{t}}] = [W]\cdot [AV]\cdot [Zt_{abc}]\cdot [G1] \end{gather}\] \[\begin{eqnarray} \label{bb94} \begin{bmatrix} G1 \end{bmatrix}= \frac{1}{Zt_{ab}+Zt_{bc}+Zt_{ca}}\cdot \begin{bmatrix} Zt_{ca} & -Zt_{bc} &0 \\ Zt_{ca}& Zt_{ab}+Zt_{ca} &0 \\ -Zt_{ab}-Zt_{bc}& -Zt_{bc} & 0 \end{bmatrix} \end{eqnarray}\]广义电流方程:
\[\begin{eqnarray} \label{bb98} \begin{bmatrix} I_{ABC} \end{bmatrix}=\begin{bmatrix} AI \end{bmatrix}^{-1}\cdot \begin{bmatrix} I_{abc} \end{bmatrix}=\begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{eqnarray} [d_{\text{t}}] = \begin{bmatrix} \frac{1}{n_{\text{t}}} & 0 & 0 \\ 0 & \frac{1}{n_{\text{t}}} & 0 \\ 0 & 0 & \frac{1}{n_{\text{t}}} \end{bmatrix} \end{eqnarray}\]逆向广义电压方程:
\[\begin{eqnarray} \label{bb99} \begin{bmatrix} VLN_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{ABC} \end{bmatrix}-\begin{bmatrix} B_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} \begin{bmatrix} A_{\text{t}} \end{bmatrix}= \begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} AV \end{bmatrix}^{-1}\cdot \begin{bmatrix} D \end{bmatrix}=\frac{1}{3\cdot n_{\text{t}}}\cdot \begin{bmatrix} 2 & -1 &-1 \\ -1 & 2 &-1 \\ -1 & -1 & 2 \end{bmatrix} \label{bb100}\\ \begin{bmatrix} B_{\text{t}} \end{bmatrix}=\begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} Zt_{abc} \end{bmatrix}\cdot \begin{bmatrix} G1 \end{bmatrix} \label{bb101} \end{gather}\]开放星形-开放三角形接法
配电馈线的常见负载是单相照明负载和三相电力负载的组合。当三相负载与单相负载相比较小时,通常使用开放星形-开放三角形接法。这种连接方式仅需要两个变压器,但能为组合负载提供三相线路电压。

同样从变压器的电压方程和电流方程入手,通过推导,可以得到如下的广义方程。
广义电压方程:
\[\begin{eqnarray} \label{bb142} \begin{bmatrix} VLG_{ABC} \end{bmatrix}=\begin{bmatrix} a_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{abc} \end{bmatrix}+\begin{bmatrix} b_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} [a_{\text{t}}] = \begin{bmatrix} n_{\text{t}} & -n_{\text{t}} & 0 \\ 0 & n_{\text{t}} & -n_{\text{t}} \\ 0 & 0 & 0 \end{bmatrix} \\ [b_{\text{t}}] = \begin{bmatrix} n_{\text{t}}\cdot Zt_{ab} & 0 & 0 \\ 0 & 0 & -n_{\text{t}}\cdot Zt_{bc} \\ 0 & 0 & 0 \end{bmatrix} \end{gather}\]广义电流方程:
\[\begin{gather} \begin{bmatrix} I_{A}\\ I_{B}\\ I_{C} \end{bmatrix}=\begin{bmatrix} \frac{1}{n_{\text{t}}} & 0 &0 \\ 0&0 & -\frac{1}{n_{\text{t}}}\\ 0&0 & 0 \end{bmatrix}\cdot \begin{bmatrix} I_{a}\\ I_{b}\\ I_{c} \end{bmatrix} \label{bb145}\\ \begin{bmatrix} I_{ABC} \end{bmatrix}=\begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \label{bb146} \end{gather}\]其中:
\[\begin{eqnarray} [d_{\text{t}}] = \begin{bmatrix} \frac{1}{n_{\text{t}}} & 0 & 0 \\ 0 & 0 & -\frac{1}{n_{\text{t}}} \\ 0 & 0 & 0 \end{bmatrix} \end{eqnarray}\]逆向广义电压方程:
\[\begin{eqnarray} \label{bb152} \begin{bmatrix} VLN_{abc} \end{bmatrix}=\begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} VLL_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLG_{ABC} \end{bmatrix}-\begin{bmatrix} B_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]其中:
\[\begin{gather} \begin{bmatrix} A_{\text{t}} \end{bmatrix}=\begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} BV \end{bmatrix}= \frac{1}{3\cdot n_{\text{t}}}\cdot \begin{bmatrix} 2 &1 &0 \\ -1& 1 & 0\\ -1 &-2 &0 \end{bmatrix} \label{bb153}\\ \begin{bmatrix} B_{\text{t}} \end{bmatrix}=\begin{bmatrix} W \end{bmatrix}\cdot \begin{bmatrix} Zt_{abc} \end{bmatrix}= \frac{1}{3}\cdot \begin{bmatrix} 2\cdot Zt_{ab} &0 & - Zt_{bc}\\ - Zt_{ab}& 0 &-Zt_{bc}\\ - Zt_{ab} &0 &2\cdot Zt_{bc} \end{bmatrix} \label{bb154} \end{gather}\]按照教材中的推导我们最后得到的是考虑\(A\)相和\(B\)相接入的情况,另外两种可能的接法是使用\(B\)相和\(C\)相、\(C\)相和\(A\)相,这两者的广义矩阵与上述导出的矩阵不同。
“超前”和“滞后”接法
“超前”和“滞后”接法与开放星形-开放三角形接法相关联。
当照明变压器接在两相之中的超前相时,该接法被称为 “超前” 接法。当照明变压器接在两相之中的滞后相时,该接法被称为 “滞后” 接法。
比如,当变压器组连接到\(A\)相和\(B\)相,并且照明变压器接在\(A\)相和地之间,就被称为超前接法,因为电压\(A\)-\(G\)超前电压\(B\)-\(G\) 120\(^{\circ}\)。
戴维南等效
目前我们已经得到五种变压器接法相应的广义矩阵,在第六章短路分析里要求对变压器一次侧电路进行戴维南等效,将其等效到变压器的二次侧。下图一所示是一个通用变压器电路,图二是变压器二次侧节点上所需的戴维南等效电路。这里我们介绍一种使用了广义矩阵的通用戴维南等效电路。
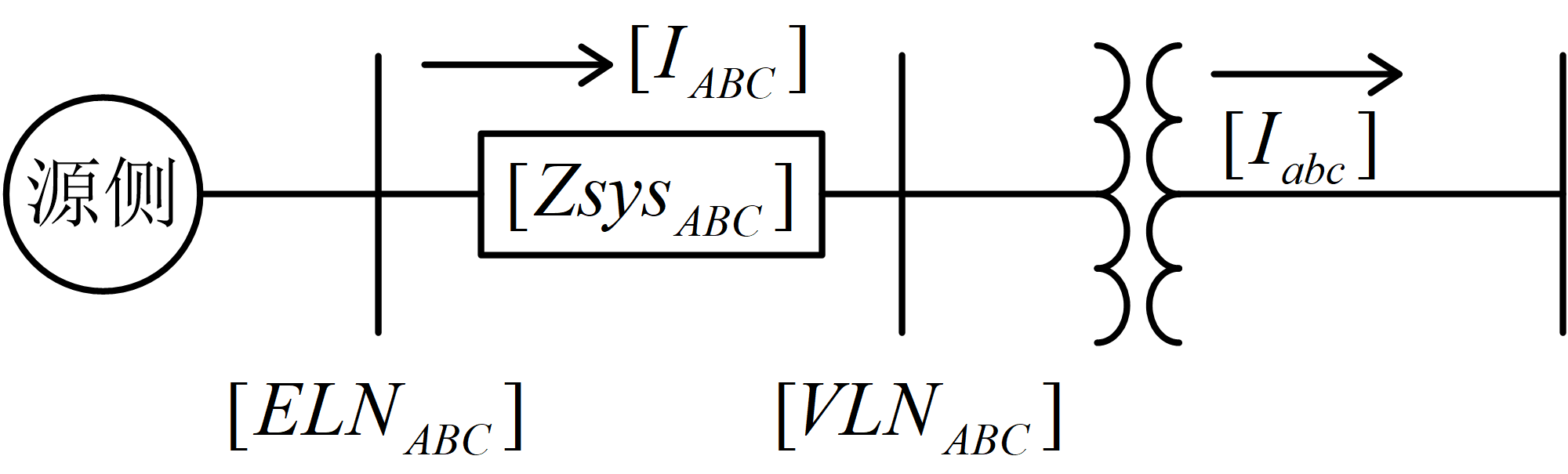
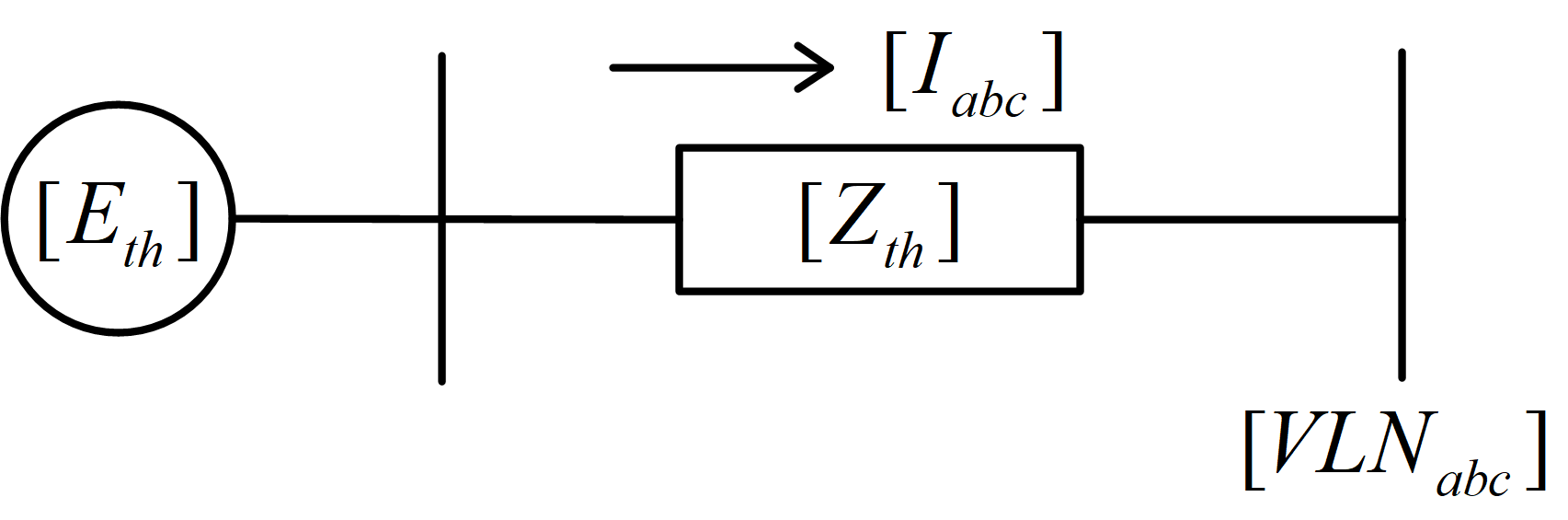
一次侧变压器等效线对中性点电压为
\[\begin{eqnarray} \label{bb155} \begin{bmatrix} VLN_{ABC} \end{bmatrix}=\begin{bmatrix} ELN_{ABC} \end{bmatrix}-\begin{bmatrix} Zsys_{ABC} \end{bmatrix}\cdot \begin{bmatrix} I_{ABC} \end{bmatrix} \end{eqnarray}\]又
\[\begin{bmatrix} I_{ABC} \end{bmatrix}=\begin{bmatrix} d_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix}\]
因此有
\[\begin{eqnarray} \label{bb156} \begin{bmatrix} VLN_{ABC} \end{bmatrix}=\begin{bmatrix} ELN_{ABC} \end{bmatrix}-\begin{bmatrix} Zsys_{ABC} \end{bmatrix}\cdot\begin{bmatrix} d_{\text{t}} \end{bmatrix} \cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]二次侧线对中性点电压为
\[\begin{eqnarray} \label{bb157} \begin{bmatrix} VLN_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} VLN_{ABC} \end{bmatrix}-\begin{bmatrix} B_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]联立以上两式可得
\[\begin{eqnarray} \label{bb158} \begin{bmatrix} VLN_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{Bmatrix} \begin{bmatrix} ELN_{ABC} \end{bmatrix}-\begin{bmatrix} Zsys_{ABC} \end{bmatrix}\cdot\begin{bmatrix} d_{\text{t}} \end{bmatrix} \cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{Bmatrix}-\begin{bmatrix} B_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} I_{abc} \end{bmatrix} \end{eqnarray}\]参考这个式子的形式,戴维南等效电压和阻抗可以定义为
\[\begin{gather} \begin{bmatrix} Eth_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} ELN_{ABC} \end{bmatrix} \label{bb159}\\ \begin{bmatrix} Zth_{abc} \end{bmatrix}=\begin{bmatrix} A_{\text{t}} \end{bmatrix}\cdot \begin{bmatrix} Zsys_{ABC} \end{bmatrix}\cdot \begin{bmatrix} d_{\text{t}} \end{bmatrix}+\begin{bmatrix} B_{\text{t}} \end{bmatrix} \label{bb160} \end{gather}\]最后给出的戴维南等效电压和阻抗的定义具有通用性,可用于所有变压器接法。教材中例题4.5给出了一个计算戴维南等效电路的例子。