智能配电网络建模与分析

配电线路模型

2020年

本次课程内容

三相线路的串联阻抗
三相线路的并联导纳
配电网络的线路模型

架空线和地下线的串联阻抗

单相、两相（$V$相）或三相配电线的串联阻抗包括导体的电阻以及由导体周围的磁场产生的自感和互感电抗。

首先讨论架空线的串联阻抗，然后讨论地下线的串联阻抗。

阻抗的感抗（自感和互感）分量是导体周围总磁场的函数。图为$n$个导体的磁场示意图，其中导体编号从1到$n$。每个导体上流过的电流都会产生磁通量线。假定电流的方向为垂直纸面向外，并且各导体上的电流和为0，即

\[\begin{eqnarray} \label{eps1} I_1+I_2+\cdots +I_ i+\cdots +I_n=0 \end{eqnarray}\]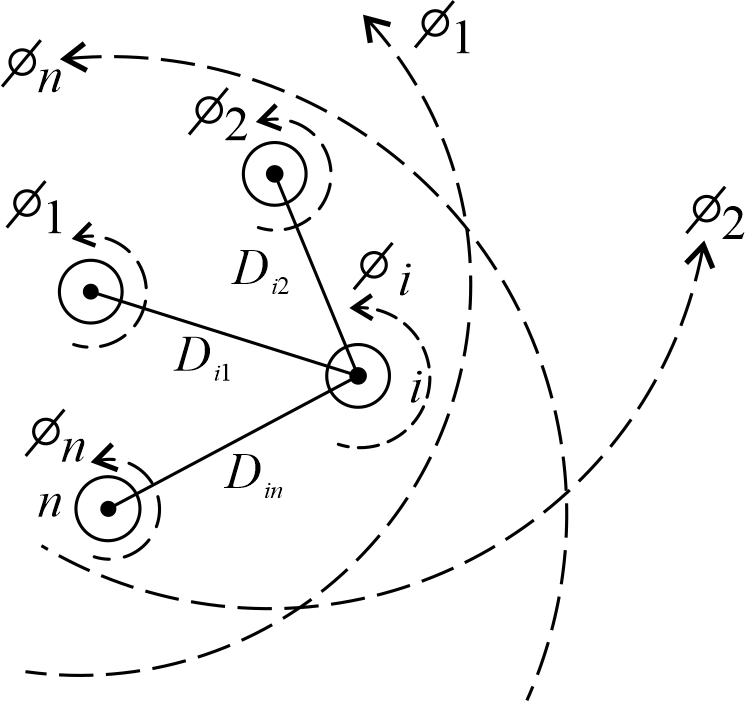 $导体磁场\label{DTCC}$

忽略内自感，则导体$i$的总磁链为

\[\begin{eqnarray} \label{eps2} \lambda _i=\frac{\mu_0}{2\pi} \left ( I_1\ln \frac{1}{D_{i1}}+I_2\ln \frac{1}{D_{i2}}+\cdots +I_i \ln \frac{1}{GMR_i} +\cdots +I_n \ln \frac{1}{D_{in}}\right ) \; \text{(Wb)} \end{eqnarray}\]

式中：$D_{in}$为导体$i$和导体$n$之间的距离(m)；$GMR_i$为导体$i$的几何平均半径。导体的几何平均半径是一个假想的筒形导体的半径，该导体的筒壁极薄，无内部磁通但其外部磁链与原导体的总磁链（内部和外部的磁链之和）相同。

导体$i$的电感包括自感以及与其他$n-1$个导体之间的互感。

导体$i$的自感：

\[\begin{eqnarray} \label{eps3} L_{ii}=\frac{\lambda _{ii}}{I_i}=\frac{\mu_0}{2\pi} \ln \frac{1}{GMR_i} \; \text{(H/m)} \end{eqnarray}\]

导体$i$与导体$n$之间的互感：

\[\begin{eqnarray} \label{eps4} L_{in}=\frac{\lambda _{in}}{I_n}=\frac{\mu_0}{2\pi} \ln \frac{1}{D_{in}} \; \text{(H/m)} \end{eqnarray}\]

三相换位情况下线路的感抗

通常情况下我们假设高压输电线已经经过换位（每相在结构上占据线的长度的三分之一）。除了换位的假设之外，我们还假设每相具有相等的负荷（对称负荷）。通过这两个假设，可以将自感和互感合并为一个相电感。

相电感：

\[\begin{eqnarray} \label{eps5} L_i=\frac{\mu_0}{2\pi}\ln \frac{D_\text{eq}}{GMR_i}\; \text{(H/m)} \end{eqnarray}\]

式中：$D_\text{eq}=\sqrt[3]{D_{ab}\cdot D_{bc}\cdot D_{ca}}\ \text{(m)}$；$D_{ab}$、$D_{bc}$、$D_{ca}$为各相之间的距离。

取频率为50Hz，真空中磁导率$\mu_0$为$4\pi\times10^{-7}$，则每相的感抗为

\[\begin{eqnarray} \label{eps7} x_i=\omega \cdot L_i=0.06283 \ln \frac{D_\text{eq}}{GM\!R_i}\; \text{(}\Omega \text{/km)} \end{eqnarray}\]

则换位三相线每相的串联阻抗为

\[\begin{eqnarray} \label{eps8} z_i=r_i+\text{j}0.06283 \ln \frac{D_\text{eq}}{GM\!R_i}\; \text{(}\Omega \text{/km)} \end{eqnarray}\]

未换位情况下线路的感抗

由于由单相、两相以及三相馈线构成的配电网络是对不对称负荷供电，因此必须保留导体的自阻抗与互阻抗特性，同时还要考虑不对称电流的接地返回路径。导体的交流电阻可直接取自导体数据表（附录A）。导体的自感和互感可用前文中的公式计算，计算的时候假定频率为50Hz，导体的长度为1km，则导体的自阻抗和互阻抗为

\[\begin{gather} \bar{z}_{ii}=r_i+\text{j}0.06283 \ln \frac{1}{GM\!R_i}\;\text{(}\Omega \text{/km)} \label{eps9} \\ \bar{z}_{ij}=\text{j}0.06283 \ln \frac{1}{D_{ij}}\;\text{(}\Omega \text{/km)} \label{eps10} \end{gather}\]

1926年，Carson建立了一套计算线路自阻抗和互阻抗的方程式（考虑电流的接地返回路径）。Carson的方法中，用一端与电源相连，另一远端接地的导体代表导线。下图中，两条线路$i$和$j$，流经的电流分别为$I_i$和$I_j$，线路的远端接地。同时假定一条线路代表电流的返回路径，其上电流为 $I_d$。在下图中，利用基尔霍夫电压定律可写出导体$i$和地之间的电压等式：

\[\begin{eqnarray} \label{eps11} V_{ig}&=&\bar{z}_{ii}\cdot I_i+\bar{z}_{ij}\cdot I_j+\bar{z}_{id}\cdot I_d-\left ( \bar{z}_{dd}\cdot I_d+\bar{z}_{di}\cdot I_i+\bar{z}_{dj}\cdot I_j \right ) \nonumber \\ ~&=&\left ( \bar{z}_{ii}-\bar{z}_{di} \right )\cdot I_i+\left ( \bar{z}_{ij}-\bar{z}_{dj}\right )\cdot I_j+\left ( \bar{z}_{id}-\bar{z}_{dd} \right )\cdot I_d \end{eqnarray}\]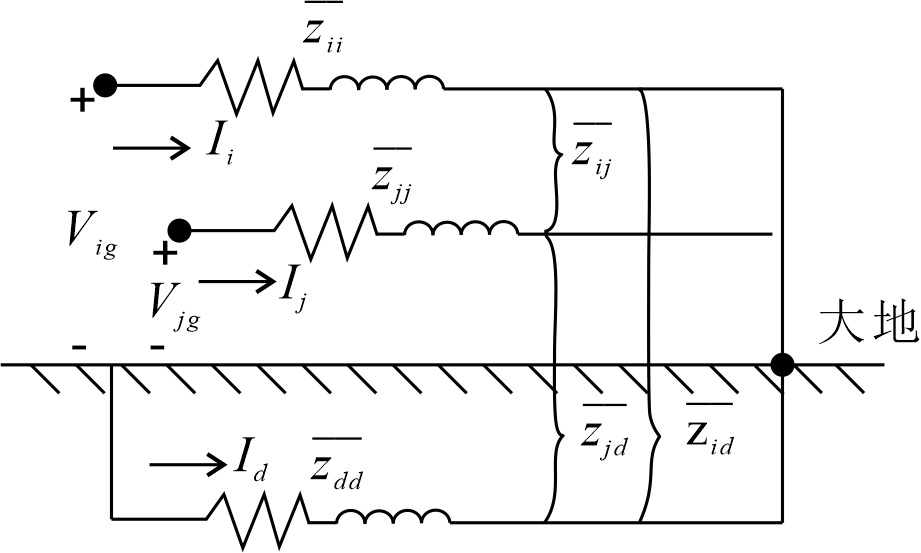 $两个导体以及地下返回路径\label{LGDT}$

由基尔霍夫电流定律得

\[\begin{eqnarray} \label{eps13} I_d=-I_i-I_j \end{eqnarray}\]

两式联立整理可得

\[\begin{eqnarray} \label{eps14} V_{ig}=\left ( \bar{z}_{ii}+\bar{z}_{dd}-\bar{z}_{di}-\bar{z}_{id} \right )\cdot I_i+\left ( \bar{z}_{ij}+\bar{z}_{dd}-\bar{z}_{dj}-\bar{z}_{id} \right )\cdot I_j \end{eqnarray}\]

一般形式为

\[\begin{eqnarray} \label{eps15} V_{ig}=\hat{z}_{ii}\cdot I_i+\hat{z}_{ij}\cdot I_j \end{eqnarray}\]

其中：

\[\begin{gather} \hat{z}_{ii}= \bar{z}_{ii}+\bar{z}_{dd}-\bar{z}_{di}-\bar{z}_{id} \label{eps16}\\ \hat{z}_{ij}= \bar{z}_{ij}+\bar{z}_{dd}-\bar{z}_{dj}-\bar{z}_{id} \label{eps17} \end{gather}\]

上式中的自阻抗和互阻抗由前面的公式计算得到。注意到，接地返回路径的影响被包含在了线路的原始自阻抗和互阻抗中。

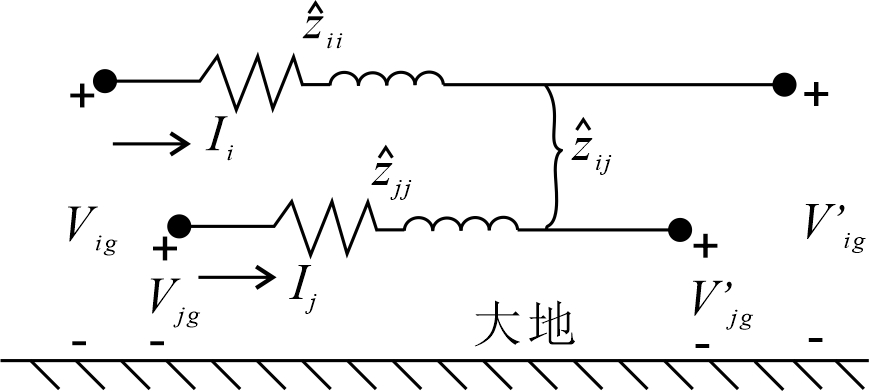
原始电路的等效电路如图所示。按前述方法计算，原始自阻抗为

\[\begin{eqnarray} \label{eps18} \hat{z}_{ii}&=&r_i+\text{j}x_{ii}+r_d+\text{j}x_{dd}-\text{j}x_{id}-\text{j}x_{di} \nonumber \\ ~&=&r_i+r_d+\text{j}0.06283\cdot \left ( \ln \frac{1}{GM\!R_i} +\ln \frac{D_{id}\cdot D_{di}}{GM\!R_d}\right ) \end{eqnarray}\]

原始互阻抗为

\[\begin{eqnarray} \label{eps19} \hat{z}_{ij}&=&\text{j}x_{ij}+r_d+\text{j}x_{dd}-\text{j}x_{dj}-\text{j}x_{id} \nonumber \\ ~&=&r_d+\text{j}0.06283\cdot \left ( \ln \frac{1}{D_{ij}} +\ln \frac{D_{id}\cdot D_{dj}}{GM\!R_d}\right ) \end{eqnarray}\]

此时不知道大地的电阻、大地的几何平均半径以及导体到大地的距离。而Carson的方法可以解决这个问题。

$原始电路的等效电路\label{DXYS}$

Carson方程

由于配电网络本质上是不对称的，因此最准确的分析不应对导体的间距、导体尺寸和换位做出任何假设。在1926年的论文中，Carson建立了一种可以确定任意数量的架空导线的自阻抗和互阻抗的方法，该方法也可以应用于地下电缆。由于该方法的计算十分烦琐，所以并没有受到太多人的关注。随着数字计算机的出现，Carson方程才被广泛使用。

在论文中，Carson认为地球是一个无限均匀的固体，具有平坦的上表面和恒定的电阻率。在中性点接地处引入的任何末端效应在工频频率下很小，因此可以被忽略。

Carson利用了导体的镜像，也就是说，在地面上给定距离处的导体，在地面下相同位置处都具有它的镜像导体，如图所示。参照下图，原始的Carson方程由下式给出。

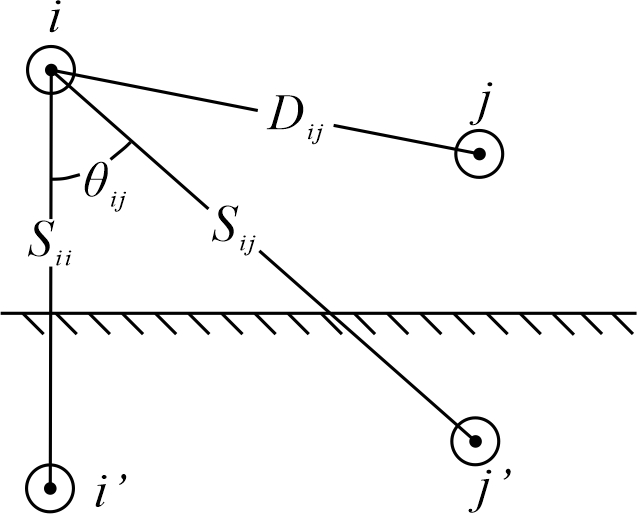
$导体及其镜像\label{DTJX}$

导体$i$的自阻抗：

\[\begin{eqnarray} \label{eps20} \hat{z}_{ii}=r_i+4\omega P_{ii}G+\text{j}\left ( X_i+2\omega G\cdot \ln \frac{S_{ii}}{RD_i} +4\omega Q_{ii}G\right )\;\text{(}\Omega \text{/km)} \end{eqnarray}\]

导体$i$和$j$之间的互阻抗：

\[\begin{eqnarray} \label{eps21} \hat{z}_{ij}=4\omega P_{ij}G+\text{j}\left (2\omega G\cdot \ln \frac{S_{ij}}{D_{ij}} +4\omega Q_{ij}G\right )\;\text{(}\Omega \text{/km)} \end{eqnarray}\]

$\hat{z}_{ii}$为导体$i$的自阻抗，单位$\Omega \text{/km}$；

$\hat{z}_{ij}$为导体$i$和$j$之间的互阻抗，单位$\Omega \text{/km}$；

$r_i$为导体$i$的电阻，单位$\Omega \text{/km}$；

$\omega =2\pi f$为系统角频率，单位rad/s； $G=1\times 10^{-4}$ $\Omega \text{/km}$；

$RD_i$为导体$i$的半径，单位m； $GMR_i$为导体$i$的几何平均半径，单位m；

$f$为系统频率，单位Hz； $\rho$为大地电阻率，单位$\Omega \cdot \text{m}$；

$D_{ij}$为导体$i$和$j$之间的距离（见图），单位m；

$S_{ij}$为导体$i$和镜像$j$之间的距离，单位m；

$\theta _{ij}$为导体$i$、$j$的镜像和导体$i$之间连线的夹角。

\[\begin{gather} X_i=2\omega G\cdot \ln \frac{RD_i}{GMR_i}\;\text{(}\Omega \text{/km)} \label{eps22}\\ P_{ij}=\frac{\pi }{8}-\frac{1}{3\sqrt{2}}k_{ij}\cos \left ( \theta _{ij} \right )+\frac{k_{ij}^{2}}{16}\cos \left ( 2\theta _{ij} \right )\left ( 0.6728+\ln \frac{2}{k_{ij}} \right ) \label{eps23}\\ Q_{ij}=-0.0386+\frac{1}{2}\ln \frac{2}{k_{ij}}+\frac{1}{3\sqrt{2}}k_{ij}\cos \left ( \theta _{ij} \right ) \label{eps24} \end{gather}\] \[\begin{equation} k_{ij}=8.565\times 10^{-4}S_{ij} \sqrt{\frac{f}{\rho }} \label{eps25} \end{equation}\]

改进的Carson方程

在导出改进的Carson方程时，只做出了两处近似。这些近似涉及与$P_{ij}$和$Q_{ij}$相关的项，即仅使用变量$P_{ij}$的第一项以及$Q_{ij}$的前两项。

\[\begin{gather} P_{ij}=\frac{\pi }{8} \label{eps26}\\ Q_{ij}=-0.03860+\frac{1}{2}\ln \frac{2}{k_{ij}} \label{eps27} \end{gather}\]

自阻抗式写为：

\[\begin{eqnarray} \label{eps28} \hat{z}_{ii}=r_i+4\omega P_{ii}G+\text{j}\left (2\omega G\cdot \ln \frac{RD_i}{GMR_i}+2\omega G\cdot \ln \frac{S_{ii}}{RD_i} +4\omega Q_{ii}G\right )\; \end{eqnarray}\]

合并同类项并化简得

\[\begin{eqnarray} \label{eps29} \hat{z}_{ii}=r_i+4\omega P_{ii}G+\text{j}2\omega G\left (\ln \frac{S_{ii}}{GMR_i} +2Q_{ii}\right )\; \end{eqnarray}\]

化简互阻抗式得：

\[\begin{eqnarray} \label{eps30} \hat{z}_{ij}=4\omega P_{ij}G+\text{j}2\omega G\left (\ln \frac{S_{ij}}{D_{ij}} +2Q_{ij}\right )\; \end{eqnarray}\]

将近似$P_{ij}$和$\omega =2\pi f$代入得

\[\begin{gather} \hat{z}_{ii}=r_i+\pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{S_{ii}}{GMR_i} +2Q_{ii}\right )\label{eps31}\\ \hat{z}_{ij}=\pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{S_{ij}}{D_{ij}} +2Q_{ij}\right )\label{eps32} \end{gather}\]

将$k_{ij}$代入$Q_{ij}$得

\[\begin{eqnarray} \label{eps33} Q_{ij}&=&-0.03860+\displaystyle\frac{1}{2}\ln \left ( \displaystyle\frac{2}{8.565\times 10^{-4}\times S_{ij}\sqrt{\displaystyle\frac{f}{\rho }}} \right ) \nonumber \\ ~&=&-0.03860+\frac{1}{2}\ln \left ( \frac{2}{8.565\times 10^{-4}} \right )+\frac{1}{2}\ln \frac{1}{S_{ij}}+\frac{1}{2}\ln \sqrt{\frac{\rho }{f}} \nonumber \\ ~&=&3.8393-\frac{1}{2}\ln S_{ij}+\frac{1}{4}\ln \frac{\rho }{f} \end{eqnarray}\]

则

\[\begin{eqnarray} \label{eps36} 2Q_{ij}=7.6786-\ln S_{ij}+\frac{1}{2}\ln \frac{\rho }{f} \end{eqnarray}\]

将$Q_{ij}$代入自阻抗式中并化简得

\[\begin{eqnarray} \label{eps37} \hat{z}_{ii}&=& r_i+\pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{S_{ii}}{GMR_i} +7.6786-\ln S_{ii}+\frac{1}{2}\ln \frac{\rho }{f}\right ) \nonumber \\ ~&=& r_i+\pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{1}{GMR_i} +7.6786+\frac{1}{2}\ln \frac{\rho }{f}\right ) \end{eqnarray}\]

将$Q_{ij}$代入互阻抗式中并化简得

\[\begin{eqnarray} \label{eps38} \hat{z}_{ij}&=&\pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{S_{ij}}{D_{ij}} +7.6786-\ln S_{ij}+\frac{1}{2}\ln \frac{\rho }{f}\right ) \nonumber \\ ~&=& \pi ^{2}fG+\text{j}4\pi fG\left (\ln \frac{1}{D_{ij}} +7.6786+\frac{1}{2}\ln \frac{\rho }{f}\right ) \end{eqnarray}\]

假设$f$为50Hz，大地电导率$\rho$=100$\;\Omega \cdot \text{m}$，则改进的Carson方程可以表示为

\[\begin{gather} \hat{z}_{ii}=r_i+0.0493+\text{j}0.0628\left ( \ln \frac{1}{GMR_i} +8.02517\right )\;\text{(}\Omega \text{/km)}\label{eps41}\\ \hat{z}_{ij}=0.0493+\text{j}0.0628\left ( \ln \frac{1}{D_{ij}} +8.02517\right )\;\text{(}\Omega \text{/km)}\label{eps42} \end{gather}\]

前式，由于大地的阻抗、几何平均半径以及与各导体之间的距离均未知，无法运用。

改进的Carson方程已经定义了缺失的参数。

两组方程的比较表明：

\[\begin{gather} r_d=0.0493\;\Omega \text{/km}\label{eps43}\\ \ln \frac{D_{id}\cdot D_{di}}{GMR_d}=\ln \frac{D_{id}\cdot D_{dj}}{GMR_d}=8.02517 \label{eps44} \end{gather}\]

改进的Carson方程将用于计算架空线和地下线的原始自阻抗和互阻抗。

架空线路原始阻抗矩阵

改进的Carson方程用于计算一个$n$行$n$列原始阻抗矩阵中的元素。架空四线接地星形配电线路将产生4×4矩阵。对于由三根同轴中性电缆组成的地下接地星形线路段，所得矩阵将为6×6。具有$m$个中性点的三相线的原始阻抗矩阵将是这种形式：

\[\begin{equation} [\hat z_{\text{primitive}}] = \begin{bmatrix} \hat z_{aa} & \hat z_{ab} & \hat z_{ac} & \mid & \hat z_{an1} & \hat z_{an2} & \hat z_{anm} \\ \hat z_{ba} & \hat z_{bb} & \hat z_{bc} & \mid & \hat z_{bn1} & \hat z_{bn2} & \hat z_{bnm} \\ \hat z_{ca} & \hat z_{cb} & \hat z_{cc} & \mid & \hat z_{cn1} & \hat z_{cn2} & \hat z_{cnm} \\ --- & --- & --- & --- & --- & --- & --- \\ \hat z_{n1a} & \hat z_{n1b} & \hat z_{n1c} & \mid & \hat z_{n1n1} & \hat z_{n1n2} & \hat z_{n1nm} \\ \hat z_{n2a} & \hat z_{n2b} & \hat z_{n2c} & \mid & \hat z_{n2n1} & \hat z_{n2n2} & \hat z_{n2nm} \\ \hat z_{nma} & \hat z_{nmb} & \hat z_{nmc} & \mid & \hat z_{nmn1} & \hat z_{nmn2} & \hat z_{nmnm} \\ \end{bmatrix} \label{4.45} \end{equation}\]

在分块形式中，上式变为

\[\begin{equation} [\hat{z}_{\text{primitive}}]=\begin{bmatrix} [\hat{z}_{ij}] &[\hat{z}_{in}] \\ [\hat{z}_{nj}] &[\hat{z}_{nn}] \end{bmatrix} \end{equation}\]

架空线路相阻抗矩阵

对于大多数应用，原始阻抗矩阵需要还原为3×3相矩阵，由三相的自阻抗和互阻抗组成。图是一个四线接地星形配电线路，可以采用一种标准的还原方法——克朗还原法进行分析。

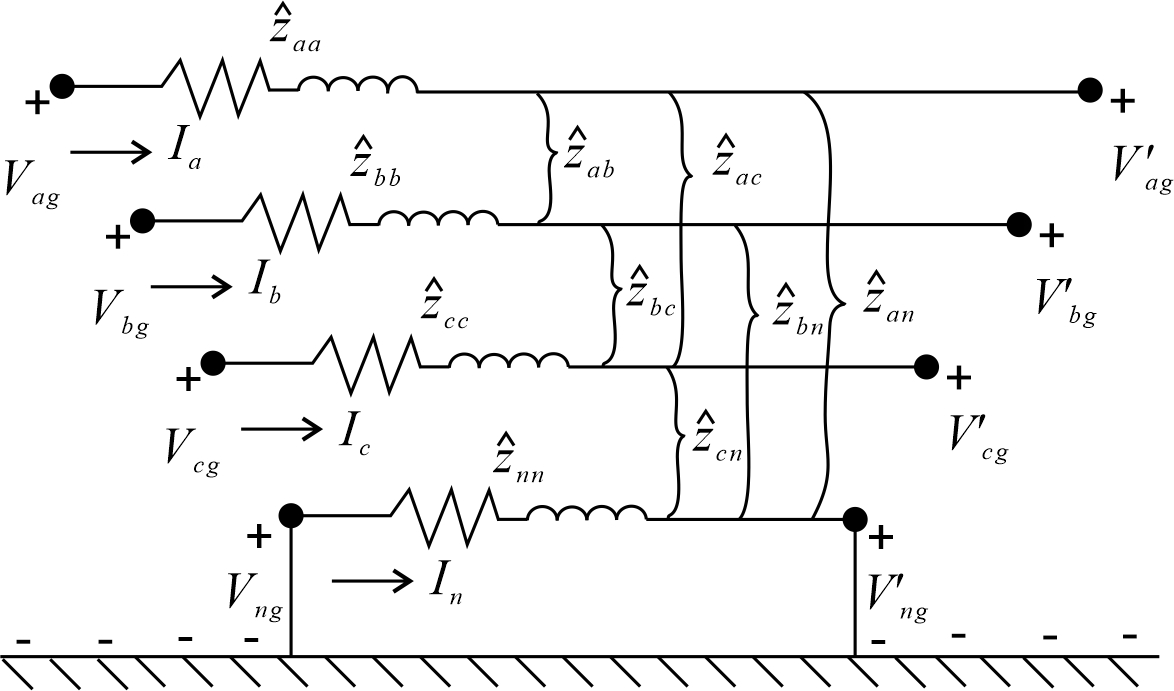
$四线接地星形线路\label{p4-5}$

如图所示，假定线路具有多点接地，由基尔霍夫电压定律得

\[\begin{equation} \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg}\\ V_{ng} \end{bmatrix}=\begin{bmatrix} V_{ag}^{'}\\ V_{bg}^{'}\\ V_{cg}^{'}\\ V_{ng}^{'} \end{bmatrix}+\begin{bmatrix} \hat{z}_{aa} & \hat{z}_{ab} & \hat{z}_{ac} & \hat{z}_{an}\\ \hat{z}_{ba} & \hat{z}_{bb} & \hat{z}_{bc} & \hat{z}_{bn}\\ \hat{z}_{ca} & \hat{z}_{cb} & \hat{z}_{cc} & \hat{z}_{cn}\\ \hat{z}_{na} & \hat{z}_{nb} & \hat{z}_{nc} & \hat{z}_{nn} \end{bmatrix}\cdot \begin{bmatrix} I_a\\ I_b\\ I_c\\ I_n \end{bmatrix} \label{4.47} \end{equation}\]

在分块形式中，上式变为

\[\begin{equation} \begin{bmatrix} [V_{abc}]\\ [V_{ng}] \end{bmatrix}=\begin{bmatrix} [V_{abc}^{'}]\\ [V_{ng}^{'}] \end{bmatrix}+\begin{bmatrix} [\hat{z_{ij}}] & [\hat{z_{in}}]\\ [\hat{z_{nj}}] & [\hat{z_{nn}}] \end{bmatrix}\cdot \begin{bmatrix} [I_{abc}]\\ [I_{n}] \label{4.48} \end{bmatrix} \end{equation}\]

由于中性点接地，电压$V_{ng}$和$V_{ng}^{'}$等于零。将这些值代入上式并将结果扩展为

\[\begin{align} \label{4.49} [V_{abc}] & = [V_{abc}^{'}]+[\hat{z_{ij}}]\cdot [I_{abc}]+[\hat{z_{in}}]\cdot [I_n] \\ \label{4.50} [0] & = [0]+[\hat{z_{nj}}]\cdot [I_{abc}]+[\hat{z_{nn}}]\cdot [I_n] \end{align}\]

求解电压$V_{ng}$方程中的[$I_n$]：

\[\begin{equation} [I_n]=-[\hat{z_{nn}}]^{-1}\cdot [\hat{z_{nj}}]\cdot [I_{abc}] \label{4.51} \end{equation}\]

将[$I_n$]代入式$[V_{abc}]$：

\[\begin{gather} \begin{split} [V_{abc}] &= [V_{abc}^{'}]+([\hat{z_{ij}}]-[\hat{z_{in}}]\cdot [\hat{z_{nn}}]^{-1}\cdot [\hat{z_{nj}}])\cdot [I_{abc}]\\ ~ &= [V_{abc}^{'}]+[z_{abc}]\cdot [I_{abc}] \end{split} \label{4.52}\\ [z_{abc}]=[\hat{z_{ij}}]-[\hat{z_{in}}]\cdot [\hat{z_{nn}}]^{-1}\cdot [\hat{z_{nj}}] \label{4.53} \end{gather}\]

式$[z_{abc}]$是克朗还原法的最终形式。最终的相阻抗矩阵变为

\[\begin{equation} [z_{abc}]=\begin{bmatrix} z_{aa} & z_{ab} & z_{ac} \\ z_{ba} & z_{bb} & z_{bc} \\ z_{ca} & z_{cb} & z_{cc} \end{bmatrix} \ \text{(}\Omega \text{/km)} \label{4.54} \end{equation}\]

对于未换位的配电线，该式的对角项元素彼此不相等，并且非对角线项元素彼此不相等，但矩阵是对称矩阵。

对于两相和单相接地星形线路系统，可以应用改进的Carson公式来产生原始阻抗矩阵，将由零元素组成的行和列添加到缺相位置处扩展为3×3矩阵。例如，由$a$相和$c$相组成的$V$相线，相阻抗矩阵是

\[\begin{equation} [z_{abc}]=\begin{bmatrix} z_{aa} & 0 & z_{ac} \\ 0 & 0 & 0 \\ z_{ca} & 0 & z_{cc} \end{bmatrix} \ \text{(}\Omega \text{/km)} \label{4.55} \end{equation}\]

$b$相单相线路的相阻抗矩阵是

\[\begin{equation} [z_{abc}]=\begin{bmatrix} 0 & 0 & 0 \\ 0 & z_{bb} & 0 \\ 0 & 0 & 0 \end{bmatrix} \ \text{(}\Omega \text{/km)} \label{4.56} \end{equation}\]

三线三角形线路的相阻抗矩阵由Carson公式决定，无须执行克朗还原步骤。

一旦电流确定，相阻抗矩阵可以用来精确地确定馈线段上的电压降。由于没有关于导体间距的近似（例如换位），精确地考虑了相间相互耦合的影响，改进Carson方程和相矩阵的应用形成了馈线的精确模型。

下图显示了三相线路段模型。注意，对于$V$相和单相线路，某些阻抗值将为零。线路矩阵形式的电压方程为

\[\begin{equation} {\begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}}_{n} = {\begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}}_{m} + \begin{bmatrix} z_{aa} & z_{ab} & z_{ac} \\ z_{ba} & z_{bb} & z_{bc} \\ z_{ca} & z_{cb} & z_{cc} \end{bmatrix} \cdot \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix} \label{4.57} \end{equation}\]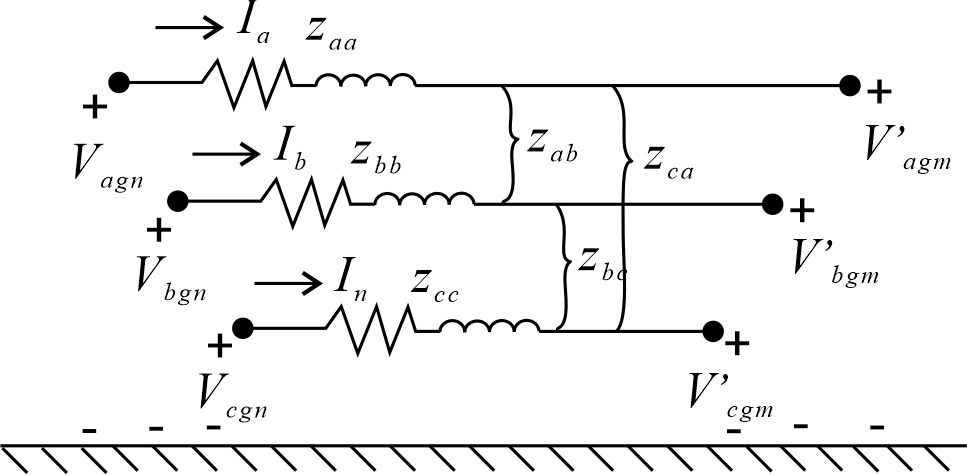 $三相线路段模型\label{p4.6}$

写成矩阵形式：

\[\begin{equation} [VLG_{abc}]_n = [VLG_{abc}]_m + [Z_{abc}]\cdot [I_{abc}] \label{4.58} \end{equation}\]

序阻抗

很多时候，馈线的分析将只使用线段的正序和零序阻抗。有两种方法可以获得这些阻抗。

第一个方法结合应用改进的Carson公式和克朗还原法来获得相阻抗矩阵。

线对地相电压与线对地序电压的关系如下：

\[\begin{equation} \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1\\ 1 & a_\text{s}^2 & a_\text{s}\\ 1 & a_\text{s} & a_\text{s}^2 \end{bmatrix}\cdot \begin{bmatrix} VLG_0\\ VLG_1\\ VLG_2 \end{bmatrix} \label{4.59} \end{equation}\]

式中：$a_\text{s} = 1.0\angle120$。

矩阵形式为

\[\begin{gather} [VLG_{abc}] = [A_\text{s}]\cdot [VLG_{012}] \label{4.60}\\ [A_\text{s}]=\begin{bmatrix} 1 & 1 & 1\\ 1 & a_\text{s}^{2} & a_\text{s}\\ 1 & a_\text{s} & a_\text{s}^{2} \end{bmatrix} \label{4.61} \end{gather}\]

相电流以相同的方式定义：

\[\begin{equation} [I_{abc}] = [A_\text{s}]\cdot [I_{012}] \label{4.62} \end{equation}\]

相电压式可用于求解作为相电压的函数的序电压：

\[\begin{gather} [VLG_{012}] = [A_\text{s}]^{-1} \cdot [VLG_{abc}] \label{4.63}\\ [A_\text{s}]^{-1}=\frac{1}{3} \cdot \begin{bmatrix} 1 & 1 & 1\\ 1 & a_\text{s} & a_\text{s}^{2}\\ 1 & a_\text{s}^{2} & a_\text{s} \end{bmatrix} \label{4.64} \end{gather}\]

将线路矩阵形式的电压方程两边乘以$[A_\text{s}]^{-1}$，并将相电流式给出的相电流代入到序域中。

\[\begin{align} [VLG_{012}]_n & = [A_\text{s}]^{-1}\cdot [VLG_{abc}]_n \nonumber \\ ~ & = [A_\text{s}]^{-1}\cdot [VLG_{abc}]_m+[A_\text{s}]^{-1}\cdot [Z_{abc}]\cdot [A_\text{s}]\cdot [I_{012}] \nonumber \\ ~ & = [VLG_{012}]_m+[Z_{012}]\cdot [I_{012}] \label{4.65} \\ [Z_{012}] & =[A_\text{s}]^{-1}\cdot [Z_{abc}]\cdot [A_\text{s}]=\begin{bmatrix} Z_{00} & Z_{01} & Z_{02}\\ Z_{10} & Z_{11} & Z_{12}\\ Z_{20} & Z_{21} & Z_{22} \end{bmatrix} \label{4.66} \end{align}\]

矩阵形式如下：

\[\begin{equation} \begin{bmatrix} VLG_0\\ VLG_1\\ VLG_2 \end{bmatrix}_n = \begin{bmatrix} VLG_0\\ VLG_1\\ VLG_2 \end{bmatrix}_m + \begin{bmatrix} Z_{00} & Z_{01} & Z_{02}\\ Z_{10} & Z_{11} & Z_{12}\\ Z_{20} & Z_{21} & Z_{22} \end{bmatrix} \cdot \begin{bmatrix} I_0\\ I_1\\ I_2 \end{bmatrix} \label{4.67} \end{equation}\]

式$[Z_{012}]$是将相阻抗转换为序阻抗的定义式。在式$[Z_{012}]$中，矩阵的对角线项是线路的序阻抗：$Z_{00}$ = 零序阻抗，$Z_{11}$ = 正序阻抗，$Z_{22}$ = 负序阻抗。非对角线项表示序之间的相互耦合关系。在理想状态下，这些非对角线项将为零。为了实现这一点，必须假设这条线已经经过换位。对于高压输电线路，有时候会接近于理想情况。当这些线换位时，相间的相互耦合相等，因此，序阻抗矩阵的非对角线项变为零。

如果假定一条线路经过换位，则相阻抗矩阵的三个对角线项相等，并且所有非对角线项均相等。通常的做法是将相阻抗矩阵的三个对角线项设置为式$[Z_{abc}]$的对角线项的平均值，并且设置非对角线项等于式$[Z_{abc}]$的非对角线项的平均值。当这样做后，自阻抗和互阻抗变为

\[\begin{gather} z_\text{s} = \frac{1}{3}\cdot (z_{aa}+z_{bb}+z_{cc})\ \text{(}\Omega/\text{km)} \label{4.68} \\ z_m = \frac{1}{3}\cdot (z_{ab}+z_{bc}+z_{ca})\ \text{(}\Omega/\text{km)} \label{4.69} \end{gather}\]

相阻抗矩阵现在定义为

\[\begin{equation} [z_{abc}] = \begin{bmatrix} z_\text{s} & z_m & z_m\\ z_m & z_\text{s} & z_m\\ z_m & z_m & z_\text{s} \end{bmatrix} \ \text{(}\Omega \text{/km)} \label{4.70} \end{equation}\]

此时序阻抗矩阵是对角阵，序阻抗可以直接确定为

\[\begin{align} z_{00} & = z_\text{s}+2 z_m \ \text{(}\Omega \text{/km)} \label{4.71} \\ z_{11} & = z_{22}=z_\text{s}-z_m \ \text{(}\Omega \text{/km)} \label{4.72} \end{align}\]

用于确定序阻抗的第二种方法是采用几何平均距离（$GMD$）的概念。

相间几何平均距离定义为

\[\begin{equation} D_{ij} = {GMD}_{ij} = \sqrt[3]{D_{ab}\cdot D_{bc}\cdot D_{ca}}\ \text{(m)} \label{4.73} \end{equation}\]

相线和中性线之间的几何平均距离定义为

\[\begin{equation} D_{in} = {GMD}_{in} = \sqrt[3]{D_{an}\cdot D_{bn}\cdot D_{cn}}\ \text{(m)} \label{4.74} \end{equation}\]

在改进的Carson方程中使用上述几何平均距离，确定线路的自阻抗和互阻抗如下：

\[\begin{gather} \hat{z}_{ii} = r_i+0.0493+\text{j}0.0628\cdot \left(\ln \frac{1}{{GMR}_i}+8.02517\right) \ \text{(}\Omega \text{/km)} \label{4.75}\\ \hat{z}_{nn} = r_n+0.0493+\text{j}0.0628\cdot \left(\ln \frac{1}{{GMR}_n}+8.02517\right) \ \text{(}\Omega \text{/km)} \label{4.76}\\ \hat{z}_{ij} = 0.0493+\text{j}0.0628\cdot \left(\ln \frac{1}{D_{ij}}+8.02517\right) \ \text{(}\Omega \text{/km)} \label{4.77}\\ \hat{z}_{in} = 0.0493+\text{j}0.0628\cdot \left(\ln \frac{1}{D_{in}}+8.02517\right) \ \text{(}\Omega \text{/km)} \label{4.78} \end{gather}\]

式中：$n$是线路中导体的数量。这四个式子定义了一个阶数为$n \times n$的矩阵。应用克朗还原和序阻抗变换，得到零序、正序和负序阻抗如下：

\[\begin{gather} z_{00} = \hat{z}_{ii}+2\cdot \hat{z}_{ij}-3\cdot \left(\frac{\hat{z}_{in}^{2}}{\hat{z}_{nn}} \right ) \ \text{(}\Omega \text{/km)} \ \qquad \qquad \label{4.79}\\ z_{11} = z_{22}=\hat{z}_{ii}-\hat{z}_{ij}=r_i+\text{j}0.06283\cdot \ln \left(\frac{D_{ij}}{GMR_i} \right )\ \text{(}\Omega \text{/km)}\label{4.80} \end{gather}\]

在换位的对称三相系统情形下，上式是计算线路阻抗的标准方程。

例题一

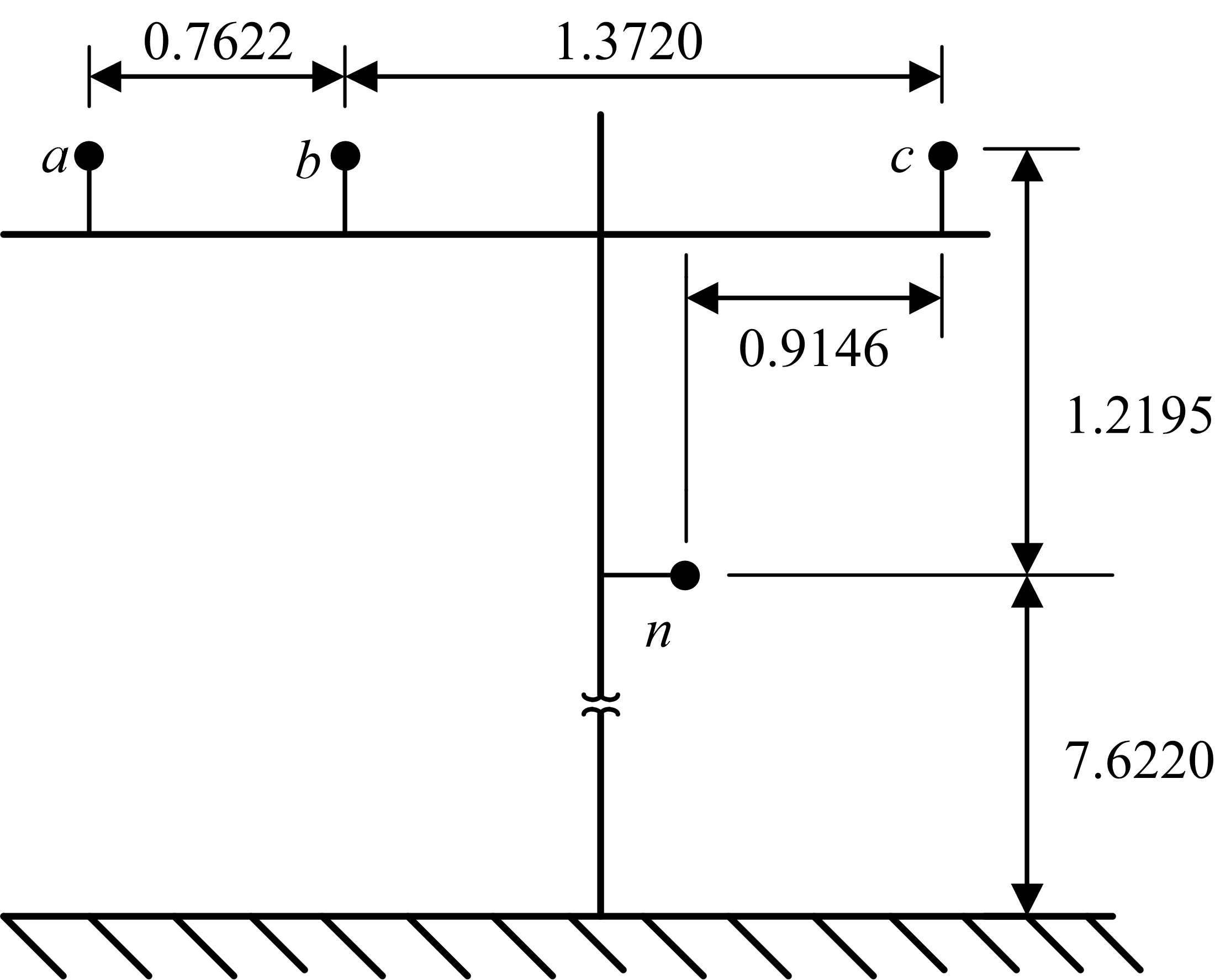
一条架空三相配电线的构造如图所示。计算相阻抗矩阵和线路的正序和零序阻抗。相线导体型号为336,400 26/7 钢芯铝绞线，中性线导体型号为4/0 6/1 钢芯铝绞线。

$架空三相配电线\label{p4.7}$

解答

从标准导体数据表（附录A）中可以得到：

336,400 26/7 钢芯铝绞线， $GMR$=0.00744 m ， $R$=0.190 $\Omega$/km
4/0 6/1 钢芯铝绞线， $GMR$=0.00248 m ， $R$=0.368 $\Omega$/km

从图可以确定导体之间的距离：

\[\begin{gather} \qquad \qquad D_{ab}=0.7622\ \text{m} & D_{bc}=1.3720\ \text{m} & D_{ca}=2.1342\ \text{m} \\ \qquad \qquad D_{an}=1.7247\ \text{m} & D_{bn}=1.3025\ \text{m} & D_{cn}=1.5244\ \text{m} \\ \end{gather}\]

将改进的Carson公式应用于自阻抗的计算，$a$相的自阻抗为

\[\begin{align} {\hat{z}}_{aa} & =0.190+0.0493+\text{j}0.0628 \left(\ln \frac{1}{0.00744}+8.02517\right) \notag \\ & = 0.2393+\text{j}0.8118 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

将改进的Carson公式应用于互阻抗的计算，$a$相和$b$相之间的互阻抗：

\[\begin{align} {\hat{z}}_{ab} & = 0.0493+\text{j}0.0628 \left(\ln \frac{1}{0.7622}+8.02517\right) \notag \\ & = 0.0493+\text{j}0.5210 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

将公式应用于其他自阻抗和互阻抗项的计算得到原始阻抗矩阵：

\[ [\hat{z}] = \begin{bmatrix} 0.2393+\text{j}0.8118 & 0.0493+\text{j}0.5210 & 0.0493+\text{j} 0.4564 & 0.0493+\text{j}0.4698\\ 0.0493+\text{j}0.5210 & 0.2393+\text{j}0.8118 & 0.0493+\text{j}0.4841 & 0.0493+\text{j}0.4874\\ 0.0493+\text{j} 0.4564 & 0.0493+\text{j}0.4841 & 0.2393+\text{j}0.8118 & 0.0493+\text{j}0.4775\\ 0.0493+\text{j}0.4698 & 0.0493+\text{j}0.4874 & 0.0493+\text{j}0.4775 & 0.4173+\text{j}0.8807 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

分块形式的原始阻抗矩阵是

\[\begin{align} [\hat{z}_{ij}] & = \begin{bmatrix} 0.2393+\text{j}0.8118 & 0.0493+\text{j}0.5210 & 0.0493+\text{j}0.4564 \\ 0.0493+\text{j}0.5210 & 0.2393+\text{j}0.8118 & 0.0493+\text{j}0.4841 \\ 0.0493+\text{j}0.4564 & 0.0493+\text{j}0.4841 & 0.2393+\text{j}0.8118 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \\ [\hat{z}_{in}] & = \begin{bmatrix} 0.0493+\text{j}0.4698 \\ 0.0493+\text{j}0.4874 \\ 0.0493+\text{j}0.4775 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \\ [\hat{z}_{nn}] &= [0.4173+\text{j}0.8807] \ \text{(}\Omega \text{/km)} \notag \\ [\hat{z}_{nj}] &= \begin{bmatrix} 0.0493+\text{j}0.4698 & 0.0493+\text{j}0.4874 & 0.0493+\text{j}0.4775 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \end{align}\]

应用克朗还原法得到相阻抗矩阵：

\[\begin{align} [z_{abc}] & = [\hat{z}_{ij}]-[\hat{z}_{in}]\cdot [\hat{z}_{nn}]^{-1}\cdot [\hat{z}_{nj}] \notag \\ ~ & = \begin{bmatrix} 0.2923+\text{j}0.5890 & 0.1051+\text{j}0.2902 & 0.1035+\text{j}0.2301\\ 0.1051+\text{j}0.2902 & 0.2980+\text{j}0.5727 & 0.1064+\text{j}0.2496\\ 0.1035+\text{j}0.2301 & 0.1064+\text{j}0.2496 & 0.2948+\text{j}0.5819 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \end{align}\]

将相阻抗矩阵转换为序阻抗矩阵：

\[\begin{align} [z_{012}] &　= [A_\text{s}]^{-1}\cdot [z_{abc}]\cdot [A_\text{s}] \notag \\　 ~ & = \begin{bmatrix} 0.5050+\text{j}1.0945 & 0.0126+\text{j}0.0060 & -0.0167+\text{j}0.0088\\ -0.0167+\text{j}0.0088 & 0.1900+\text{j}0.3246 & -0.0374-\text{j}0.0031\\ 0.0126+\text{j}0.0060 & 0.0374-\text{j}0.0031 & 0.1900+\text{j}0.3246 \end{bmatrix}　\ \text{(}\Omega \text{/km)} \notag \end{align}\]

在序阻抗矩阵中，（1,1）项是零序阻抗，（2,2）项是正序阻抗，（3,3）项是负序阻抗。（2,2）和（3,3）项是相等的，这表明对于一段线路，其正序和负序阻抗是相等的。

非对角线项不是零，意味着序之间存在相互耦合，这是相间间距不对称的结果。在非对角线项非零的情况下，表示这条线的三个序网络不是独立的。

不过，注意到非对角线项相对于对角线项较小。在本题中，可以通过用相阻抗矩阵的对角线项的平均值（0.2950 + 0.5812）替换对角项，并用非对角线项的平均值替换每个非对角线项来对线路换位进行模拟（0.1050 + 0.2567）。修正的相阻抗矩阵变为

\[ [z1_{abc}] = \begin{bmatrix} 0.2950+\text{j}0.5812 & 0.1050+\text{j}0.2567 & 0.1050+\text{j}0.2567\\ 0.1050+\text{j}0.2567 & 0.2950+\text{j}0.5812 & 0.1050+\text{j}0.2567\\ 0.1050+\text{j}0.2567 & 0.1050+\text{j}0.2567 & 0.2950+\text{j}0.5812 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

在对称分量变换方程中使用这种修正的相阻抗矩阵，得到修正的序阻抗矩阵：

\[ [z1_{012}] = \begin{bmatrix} 0.5050+\text{j}1.0946 & 0& 0\\ 0& 0.1900+\text{j}0.3245 & 0\\ 0& 0 & 0.1900+\text{j}0.3245 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

请注意，现在非对角线项全部等于零，这意味着序网络之间不存在相互耦合。还应该注意的是，修正后的零序、正序和负序阻抗与最初计算的序列阻抗相等。它意味着三相配电线可以被假定为已经换位。如果要对相间相互耦合的影响进行精确建模，则必须使用原始相阻抗矩阵。

同轴中性电缆串联阻抗

图显示了带有附加中性导体的三相地下电缆（同轴中性或带状屏蔽）的一般结构。修正后的Carson公式可以用于地下电缆，其方式与架空线相同。图的电路可以用一个7×7的原始阻抗矩阵来描述。对于没有附加中性导体的地下电缆，原始阻抗矩阵的规模是6×6。

$带有附加中性导体的三相地下电缆\label{p4.8}$

两种常见的地下电缆类型是同轴中性电缆和带屏蔽电缆。

为了应用修正的Carson方程，必须知道相导体和等效中性点的电阻和几何平均半径。

接下来详细介绍同轴中性电缆的串联阻抗。

图中的同轴中性电缆由一个被非金属半导体屏蔽层所覆盖的中性线导体组成，绝缘材料与之结合在一起，绝缘材料被半导体绝缘屏蔽层覆盖。同轴中性的实心股线以均匀间距螺旋缠绕着半导体绝缘屏蔽层。一些电缆有一个绝缘护套环绕中性线。

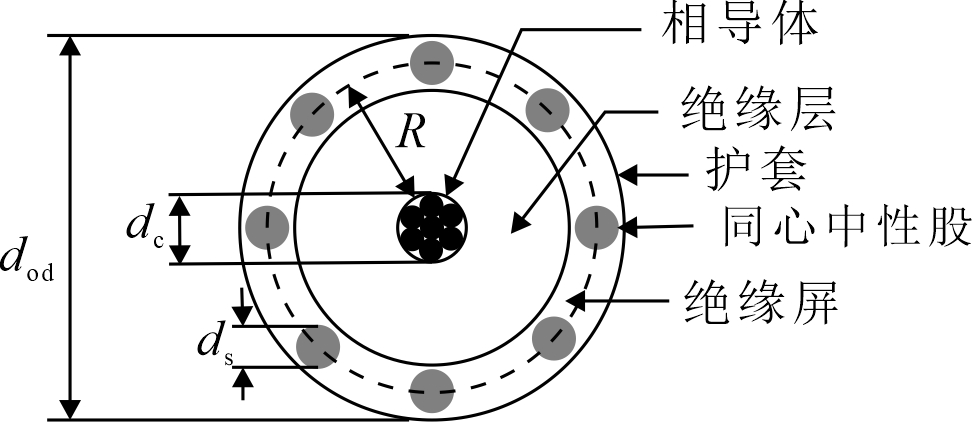
$同轴中性电缆\label{p4.9}$

为了将Carson公式应用于这条电缆，需要从附录B中获得以下数据：

$d_\text{c}$ = 相导体直径（cm）

$d_{\text{od}}$ = 同轴中性电缆的直径（cm）

$d_\text{s}$ = 同轴中性线的直径（cm）

${GMR}_\text{c}$ = 相线的几何平均半径（m）

${GMR}_\text{s}$ = 中性线几何平均半径（m）

$r_\text{c}$ = 相导体电阻（$\Omega$/km）

$r_\text{s}$ = 固体中性线的电阻（$\Omega$/km）

$k$ = 同轴中性线的数量

相线和中性线的几何平均半径可从标准导体数据表（附录A）中获得。

同轴中性线的等效几何平均半径$GMR$使用高压输电线路中采用的成束导线的几何平均半径的公式计算：

\[\begin{equation} {GMR}_{\text{cn}} = \sqrt[k]{{GMR}_\text{s}\cdot k\cdot R^{k-1}} \ \text{(m)} \label{4.81} \end{equation}\]

式中：$R$为穿过股线中心的圆的半径，用下式计算。

\[\begin{equation} R=\frac{d_{\text{od}}-d_\text{s}}{200}\ \text{(m)} \label{4.82} \end{equation}\]

同轴中性线的等效电阻为

\[\begin{equation} r_{\text{cn}} = \frac{r_\text{s}}{k} \ \text{(}\Omega \text{/km)} \label{4.83} \end{equation}\]

同轴中性线到它自己的相导体间距$D_{ij}$ = $R$。

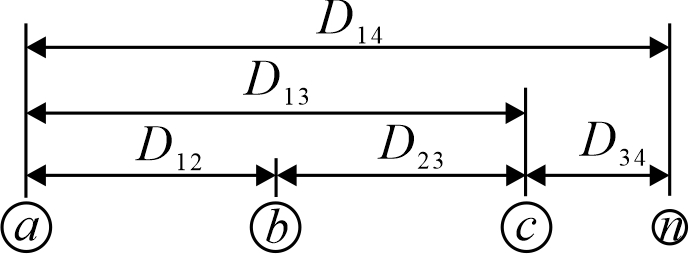
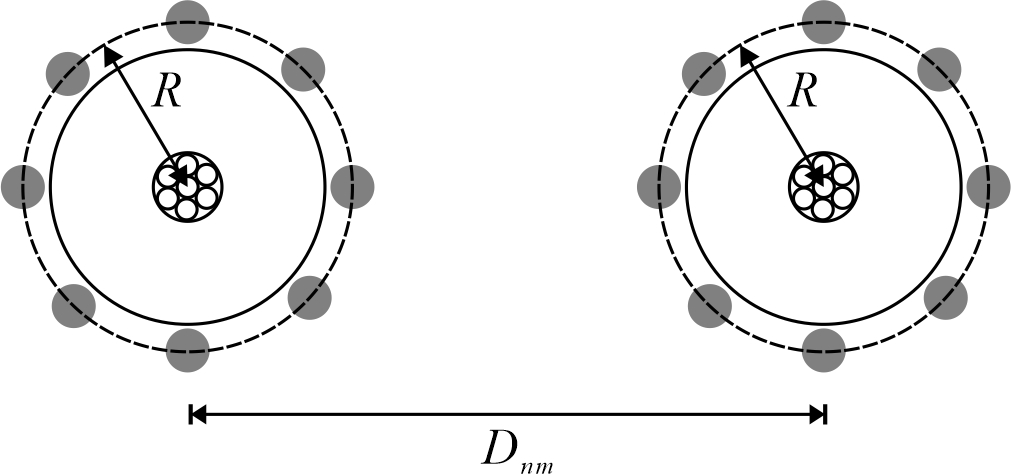
下图显示了两同轴中性电缆的几何关系。同轴中性线和相邻相导体之间的几何平均距离由以下公式得到：

\[\begin{equation} D_{ij} = \sqrt[k]{D_{nm}^{k}-R^k} \ \text{(m)} \label{4.84} \end{equation}\]

式中：$D_{nm}$为相间导体中心到中心的距离。对于埋在沟槽中的电缆，电缆之间的距离远大于半径$R$，因此可以假定方程中的$D_{ij}$等于$D_{nm}$。对于管道中的电缆，这个假设不成立。

$两同轴中性电缆几何关系\label{p4.10}$

在应用修正的Carson公式时，导体和中性线的编号非常重要。例如，具有附加中性导体的三相地下线路必须编号为：

1-相导体 #1，2-相导体 #2，3-相导体 #3，4-导体中性线 #1，5-导体中性线 #2，6-导体中性线 #3，7-附加中性导体（如果存在）。

例题二

三个同轴中性电缆埋在沟槽中，如图所示。电缆为电压等级为15 kV，相导体型号为250000 CON LAY 铝合金，中性线为13股14号退火涂层铜线（1/3中性）。中性线上的电缆外径$d_\text{od}$为3.2766 cm（附录B）。计算相阻抗矩阵和序阻抗矩阵。

$三相同轴中性电缆\label{p4.11}$

解答

导体数据表（附录A）中的相线和中性线的数据如下：

250000 铝合金相导体：${GMR}_\text{c}$ = 0.005212 m，$d_\text{c}$ = 1.4402 cm，$r_\text{c}$ = 0.2548 $\Omega$/km

14号铜中性线：${GMR}_\text{s}$ = 0.000634 m，$d_\text{s}$ = 0.162814 cm，$r_\text{s}$ = 9.2411 $\Omega$/km

穿过股线中心的圆的半径为

\[\begin{equation*} R = \frac{d_{\text{od}}-d_\text{s}}{200} = 0.01557 \ \text{(m)} \end{equation*}\]

同轴中性线的等效几何平均半径$GMR$计算如下：

\[{GMR}_{\text{cn}} = \sqrt[k]{GMR_\text{s}\cdot k\cdot R^{k-1}} = \sqrt[13]{0.000634\times 13\times 0.01557^{13-1}} = 0.01483 \ \text{(m)}\]

同轴中性线的等效电阻是：

\[\begin{equation*} r_{\text{cn}} = \frac{r_\text{s}}{k} = 0.7109 \ \text{(}\Omega \text{/km)} \end{equation*}\]

相导线编号为1、2、3，同轴中性线编号为4、5、6。导体对导体和同轴中性线对同轴中性线的间距是：

\[\begin{gather*} D_{12} = D_{21} = D_{45} = D_{54} =0.1524 \ \text{(m)}\\ D_{23} = D_{23} = D_{56} = D_{65} =0.1524 \ \text{(m)}\\ D_{31} = D_{13} = D_{64} = D_{46} =0.3048 \ \text{(m)} \end{gather*}\]

导体和同轴中性线之间的距离是：

\[D_{14} = D_{25} = D_{36} = R =0.01557 \ \text{(m)}\]

由于半径$R$比电缆之间的间距小得多，所以同轴中性线与相邻相线之间的距离就是导线之间的中心距：

\[\begin{gather*} D_{15} = D_{51} =0.1524 \ \text{(m)}\\ D_{26} = D_{62} =0.1524 \ \text{(m)}\\ D_{61} = D_{16} =0.3048 \ \text{(m)} \end{gather*}\]

位置1电缆的自阻抗为

\[\begin{align} \hat{z}_{11} & = 0.2548+0.0493+\text{j}0.0628 \left(\ln\frac{1}{0.005212}+8.02517 \right ) \notag \\ & = 0.3041+\text{j}0.8341\ \text{(}\Omega \text{/km)} \notag \end{align}\]

1号同轴中性线的自阻抗为

\[\begin{align} \hat{z}_{44} & = 0.7109+0.0493+\text{j}0.0628\left(\ln\frac{1}{0.01483}+8.02517 \right ) \notag \\ & = 0.7602+\text{j}0.7684\ \text{(}\Omega \text{/km)} \notag \end{align}\]

1号电缆和2号电缆之间的互阻抗为

\[\hat{z}_{12} = 0.0493+\text{j}0.0628 \left(\ln\frac{1}{0.1524}+8.02517 \right )= 0.0493+\text{j}0.6221\ \text{(}\Omega \text{/km)}\]

1号电缆与其同轴中性线之间的互阻抗为

\[\hat{z}_{14} = 0.0493+\text{j}0.0628 \left(\ln\frac{1}{0.01557}+8.02517 \right )= 0.0493+\text{j}0.7654\ \text{(}\Omega \text{/km)}\]

1号电缆的同轴中性线和2号电缆的同轴中性线之间的互阻抗为

\[\hat{z}_{45} = 0.0493+\text{j}0.0628 \left(\ln\frac{1}{0.1524}+8.02517 \right )= 0.0493+\text{j}0.6221\ \text{(}\Omega \text{/km)}\]

继续应用修正的Carson方程，得到一个6×6原始阻抗矩阵，矩阵的分块形式如下：

\[\begin{align} [\hat{z}_{ij}] & = \begin{bmatrix} 0.3041+\text{j}0.8341 & 0.0493+\text{j}0.6221 & 0.0493+\text{j}0.5786 \\ 0.0493+\text{j}0.6221 & 0.3041+\text{j}0.8341 & 0.0493+\text{j}0.6221 \\ 0.0493+\text{j}0.5786 & 0.0493+\text{j}0.6221 & 0.3041+\text{j}0.8341 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \\ [\hat{z}_{in}] & = \begin{bmatrix} 0.0493+\text{j}0.7654 & 0.0493+\text{j}0.6221 & 0.0493+\text{j}0.5786 \\ 0.0493+\text{j}0.6221 & 0.0493+\text{j}0.7654 & 0.0493+\text{j}0.6221 \\ 0.0493+\text{j}0.5786 & 0.0493+\text{j}0.6221 & 0.0493+\text{j}0.7654 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \\ [\hat{z}_{nj}] & = [\hat{z}_{in}]^{\text{T}} \notag \\ [\hat{z}_{nn}] & = \begin{bmatrix} 0.7602+\text{j}0.7684 & 0.0493+\text{j}0.6221 & 0.0493+\text{j}0.5786 \\ 0.0493+\text{j}0.6221 & 0.7602+\text{j}0.7684 & 0.0493+\text{j}0.6221 \\ 0.0493+\text{j}0.5786 & 0.0493+\text{j}0.6221 & 0.7602+\text{j}0.7684 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \end{align}\]

使用克朗还原法，得到相阻抗矩阵：

\[\begin{align} [z_{abc}] & = [\hat{z}_{ij}]-[\hat{z}_{in}]\cdot [\hat{z}_{nn}]^{-1}\cdot [\hat{z}_{nj}] \notag \\ ~ & = \begin{bmatrix} 0.4838+\text{j}0.2482 & 0.1994+\text{j}0.0311 & 0.1832+\text{j}0.0050\\ 0.1994+\text{j}0.0311 & 0.4813+\text{j}0.2253 & 0.1994+\text{j}0.0311\\ 0.1832+\text{j}0.0050 & 0.1994+\text{j}0.0311 & 0.4838+\text{j}0.2482 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \end{align}\]

同轴中性三相线的序阻抗矩阵由公式确定：

\[\begin{align} [z_{012}] & = [A_\text{s}]^{-1}\cdot [z_{abc}]\cdot [A_\text{s}] \notag \\ ~ & = \begin{bmatrix} 0.8709+\text{j}0.2854 & -0.0013-\text{j}0.0045 & -0.0032+\text{j}0.0034\\ -0.0032+\text{j}0.0034 & 0.2890+\text{j}0.2182 & -0.0159+\text{j}0.0226\\ -0.0013-\text{j}0.0045 & 0.0275+\text{j}0.0025 & 0.2890+\text{j}0.2182 \end{bmatrix}　\ \text{(}\Omega \text{/km)} \notag \end{align}\]

带屏蔽电缆

下图显示了带屏蔽电缆的简单细节。

电缆由被非金属半导体屏蔽层覆盖的中心相导体构成，非金属半导体屏蔽层上粘连着绝缘材料。屏蔽层是裸铜丝带，螺旋地包围在绝缘层外，绝缘护套包围着屏蔽层。带屏蔽电缆的几个重要参数如下：

$d_\text{c}$ = 相导体直径（cm）

$d_\text{s}$ = 屏蔽层的外径（cm）

$d_{\text{od}}$ = 护套外径（cm）

$T$ = 铜带屏蔽厚度（μm）

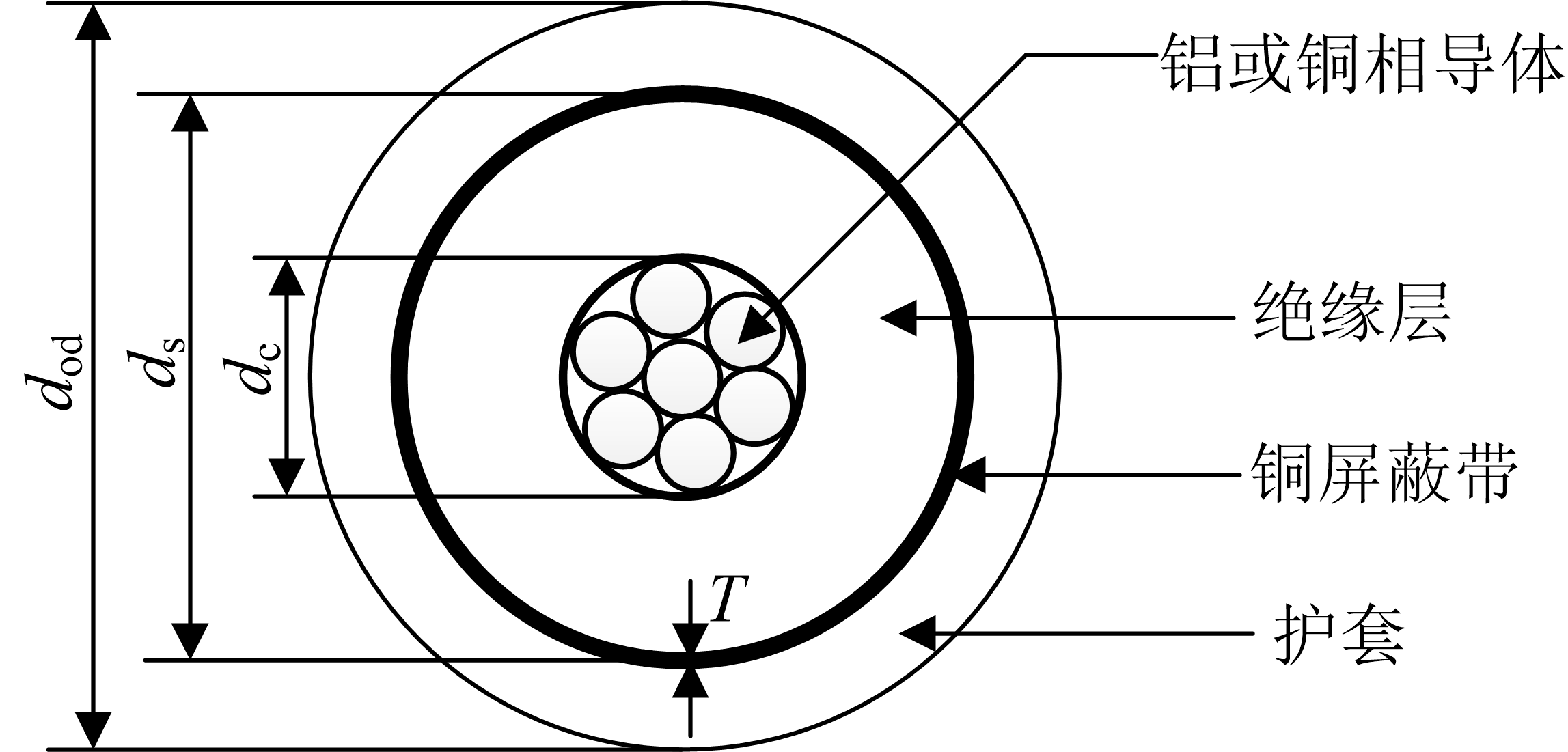
$带屏蔽电缆\label{p4.12}$

将修正的Carson公式用于计算相导体和屏蔽层导体的自阻抗，以及相导体和屏蔽层导体之间的互阻抗。相导体的电阻和几何平均半径可在数据表中找到。

屏蔽层的电阻由下式给出：

\[\begin{equation} r_{\text{sl}} = 3.1824\times 10^{10} \times \frac{\rho }{d_\text{s} T} \ \text{(}\Omega \text{/km)} \label{4.85} \end{equation}\]

式中的电阻率$\rho$取在50°C时的值，单位$\Omega$$\cdot$m。

屏蔽层的几何平均半径$GMR$是穿过屏蔽层中间的圆的半径，由下式给出：

\[\begin{equation} GMR_{\text{sl}} = \frac{d_\text{s}-\frac{T}{10000}}{2} \ \text{(cm)} \label{4.86} \end{equation}\]

屏蔽层与导体和其他屏蔽层之间的各种间距如下所示：

屏蔽层与自己的相导体的间距$D_{ii}=GMR_{\text{sl}}=$屏蔽中点的半径(cm)
屏蔽层与相邻的屏蔽层的间距$D_{ij}=$相导体之间的中心距(cm)
屏蔽层与相邻的相导体的间距$D_{ij}=$相导体之间的中心距(cm)

例题三

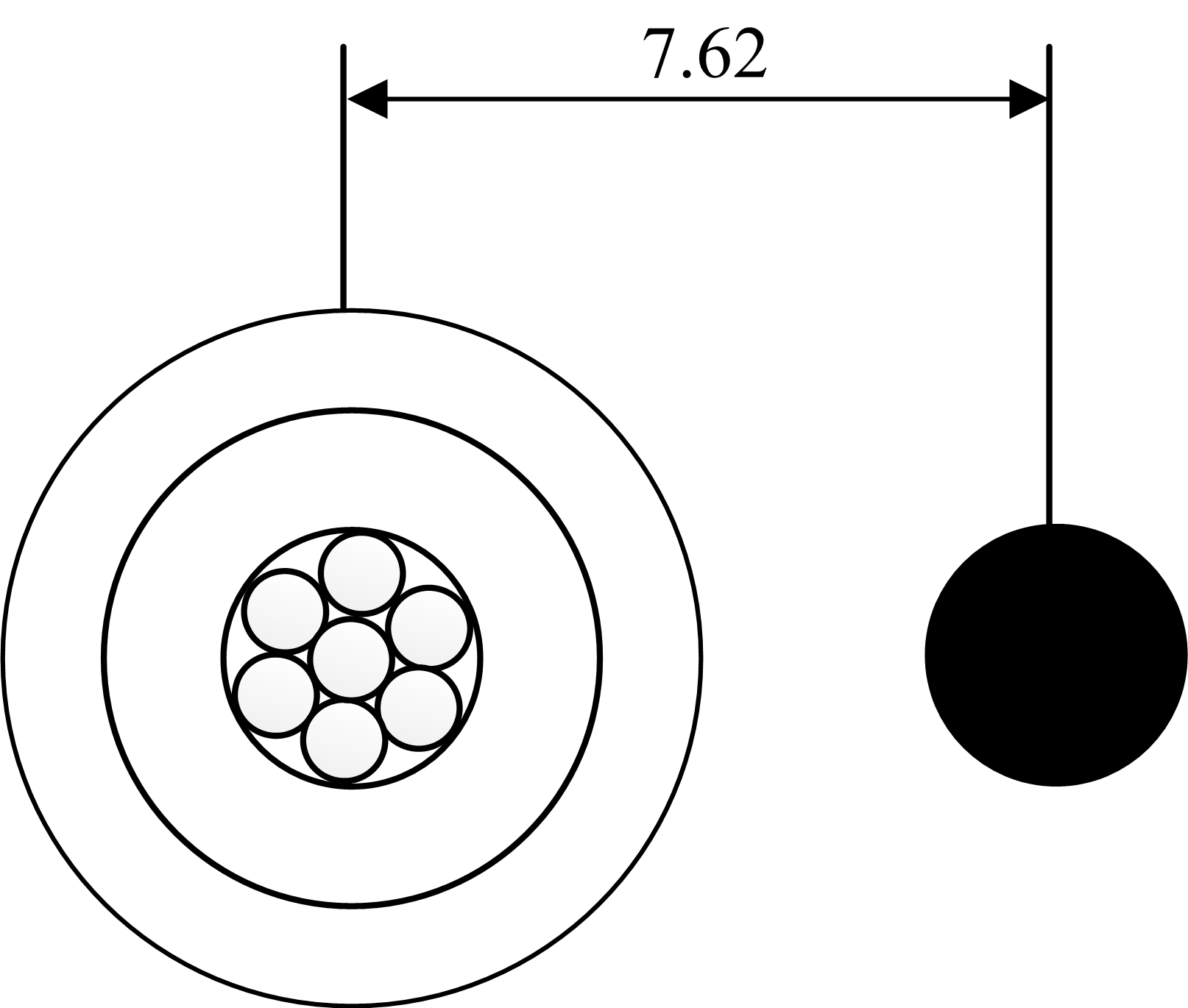
单相电路由1/0 铝合金绝缘带屏蔽电缆和1/0 铜中性导体组成，如图所示，单相线连接到$b$相。计算相阻抗矩阵，假设$\rho$ = 2.3715×10$^{-8}$ $\Omega\cdot$m。

$带中性线的单相带屏蔽电缆\label{p4.13}$

解答

电缆参数：屏蔽层外径 $d_\text{s}$ = 2.2352 cm，电阻：0.6027 $\Omega$/km，几何平均半径$GMR_p$ = 0.003383 m，屏蔽层厚度 $T$ =127 $\mu \text{m}$。

中性线参数：1/0 铜，七股，电阻：0.3772 $\Omega$/km，$GMR_n$ = 0.003392 m，电缆和中性线间距 $D_{nm}$ = 7.62 cm。

计算屏蔽层的电阻：

\[ r_{\text{sl}} = 3.1824\times 10^{10}\frac{\rho }{d_\text{s}\cdot T} = 3.1824\times 10^{10} \times \frac{2.3715\times 10^{-8}}{2.2352\cdot 127} =2.6586\ \text{(}\Omega \text{/km)} \]

计算屏蔽层的$GMR$：

\[ GMR_{\text{sl}} = \frac{d_\text{s}-\frac{T}{10000}}{2} = \frac{2.2352-\frac{127}{10000}}{2} = 1.11 \ \text{(cm)} \]

对导体进行编号：1号为1/0 铝合金导线，2号为屏蔽层，3号为1/0 铜，接地。

修正Carson公式中采用的间距为

\[\begin{align} D_{12} & = GMR_{\text{sl}} = 1.11\ \text{(cm)} \notag \\ D_{13} & = 7.62\ \text{cm} \notag \end{align}\]

1号导线的自阻抗：

\[\begin{align} {\hat{z}}_{11} & = 0.6027+0.0493+\text{j}0.0628 \ln \left(\frac{1}{0.003383}+8.02517\right) \notag \\ & = 0.6520+\text{j}0.8612 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

1号导线和2号屏蔽层之间的互阻抗为

\[\begin{align} {\hat{z}}_{12} & = 0.0493+\text{j}0.0628 \ln \left(\frac{1}{1.11}+8.02517\right) \notag \\ & = 0.0493+\text{j}0.4974 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

2号屏蔽层的自阻抗为

\[\begin{align} {\hat{z}}_{22} & = 2.6586+0.0493+\text{j}0.0628 \ln \left(\frac{1}{1.11}+8.02517\right) \notag \\ & = 2.7079+\text{j}0.4974 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

计算得到原始阻抗矩阵为

\[ [\hat{z}] = \begin{bmatrix} 0.6520+\text{j}0.8612 & 0.0493+\text{j}0.4974 & 0.0493+\text{j}0.3764\\ 0.0493+\text{j}0.4974 & 2.7079+\text{j}0.4974 & 0.0493+\text{j}0.3764\\ 0.0493+\text{j}0.3764 & 0.0493+\text{j}0.3764 & 0.4265+\text{j}0.8611 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

写成分块形式：

\[\begin{align} [\hat{z}_{ij}] & = \begin{bmatrix} 0.6520+\text{j}0.8612 \end{bmatrix} \notag \\ [\hat{z}_{in}] & = \begin{bmatrix} 0.0493+\text{j}0.4974 & 0.0493+\text{j}0.3764 \end{bmatrix} \notag \\ [\hat{z}_{nj}] & = \begin{bmatrix} 0.0493+\text{j}0.4974 \\ 0.0493+\text{j}0.3764 \end{bmatrix} \notag \\ [\hat{z}_{nn}] &= \begin{bmatrix} 2.7079+\text{j}0.4974 & 0.0493+\text{j}0.3764\\ 0.0493+\text{j}0.3764 & 0.4265+\text{j}0.8611 \end{bmatrix} \notag \end{align}\]

应用克朗还原法得到一个阻抗，它表示带屏蔽电缆和中性线的等效单相阻抗：

\[\begin{align} z_{1p} & = [\hat{z}_{ij}]-[\hat{z_{in}}]\cdot [\hat{z}_{nn}]^{-1}\cdot [\hat{z}_{nj}] \notag \\ ~ & = 0.7210+\text{j}0.6889 \ \text{(}\Omega \text{/km)} \notag \end{align}\]

由于单相线在$b$相上，所以相阻抗矩阵为

\[ [z_{abc}] = \begin{bmatrix} 0 & 0 & 0\\ 0 & 0.7210+\text{j}0.6889 & 0\\ 0 & 0 & 0 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

架空线路与地下线路的并联导纳

线路的并联导纳由电导和电纳组成。电导通常被忽略，因为它与电纳相比是非常小的。线路的电容是导体之间存在电压差的结果。带电导体产生从中心向外辐射的电场，产生的等电位线与带电导体同轴，如图所示。

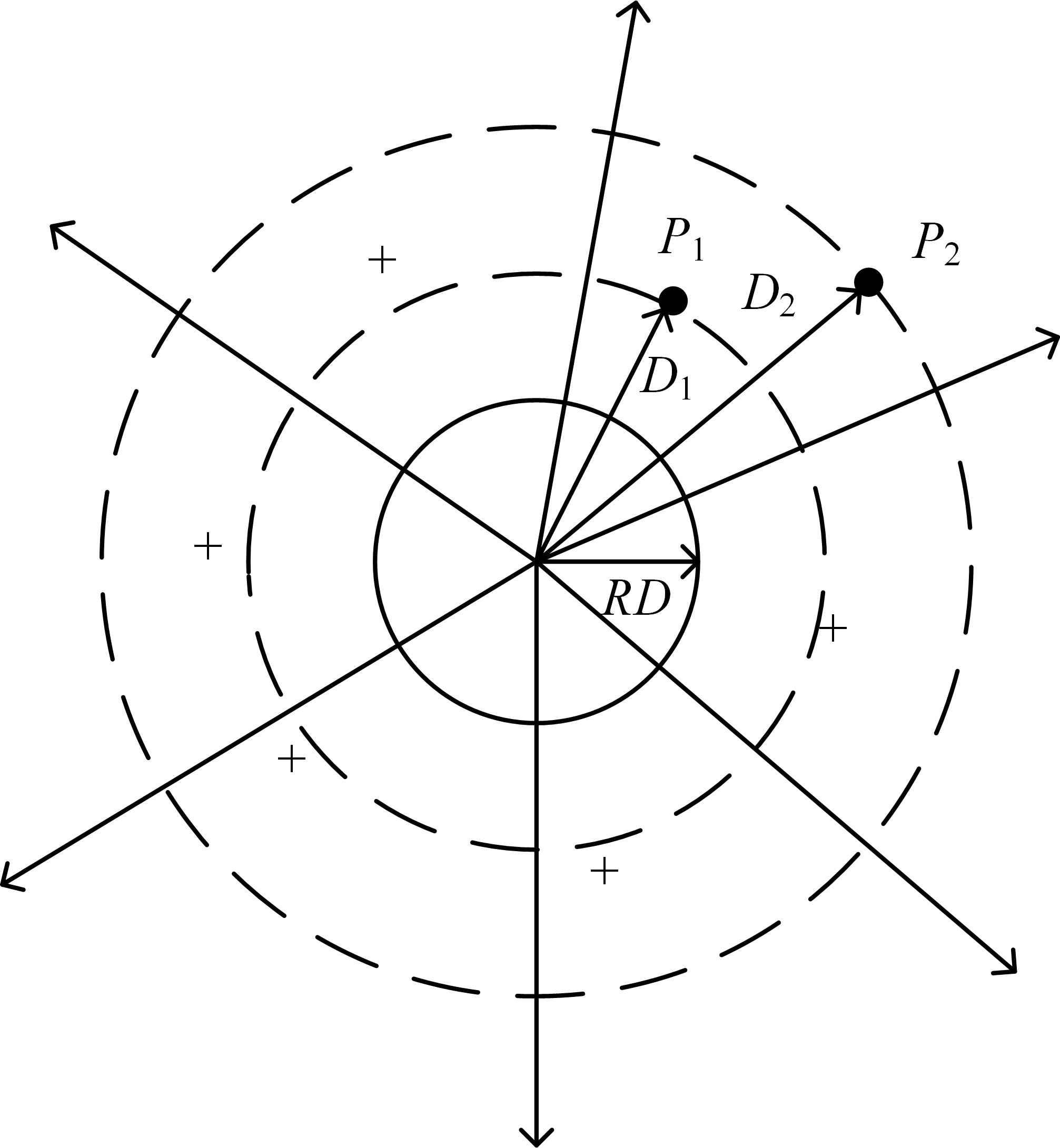
$带电圆形导体的电场\label{p5.1}$

在图中，两点之间的电压（$P_1$和$P_2$）是带电导体的电场分布所产生的。当已知两点之间的电压时，可以计算两点之间的电容。如果附近有其他带电导体，两点之间的电压将是一个关于与其他导体的距离和每个导体上的电荷量的函数。叠加原理可用于计算两点之间的电压，然后计算点间的电容。点可以是空间中的点，也可以位于两个导体的表面，或者位于导体和地的表面。

一般电压降方程

图显示了一组带正电的$N$个实心圆导体。每个导体各自带有均匀电荷密度$q$(单位：C/m)。导体$i$和导体$j$之间由所有带电导体共同作用产生的电压降由下式给出：

\[\begin{equation} V_{ij} = \frac{1}{2\pi \varepsilon }\left(q_1\ln\frac{D_{1j}}{D_{1i}}+\cdots +q_i\ln\frac{D_{ij}}{RD_i}+\cdots +q_j\ln\frac{RD_j}{D_{ij}}+\cdots +q_N\ln\frac{D_{Nj}}{D_{Ni}}\right ) \label{5.1} \end{equation}\]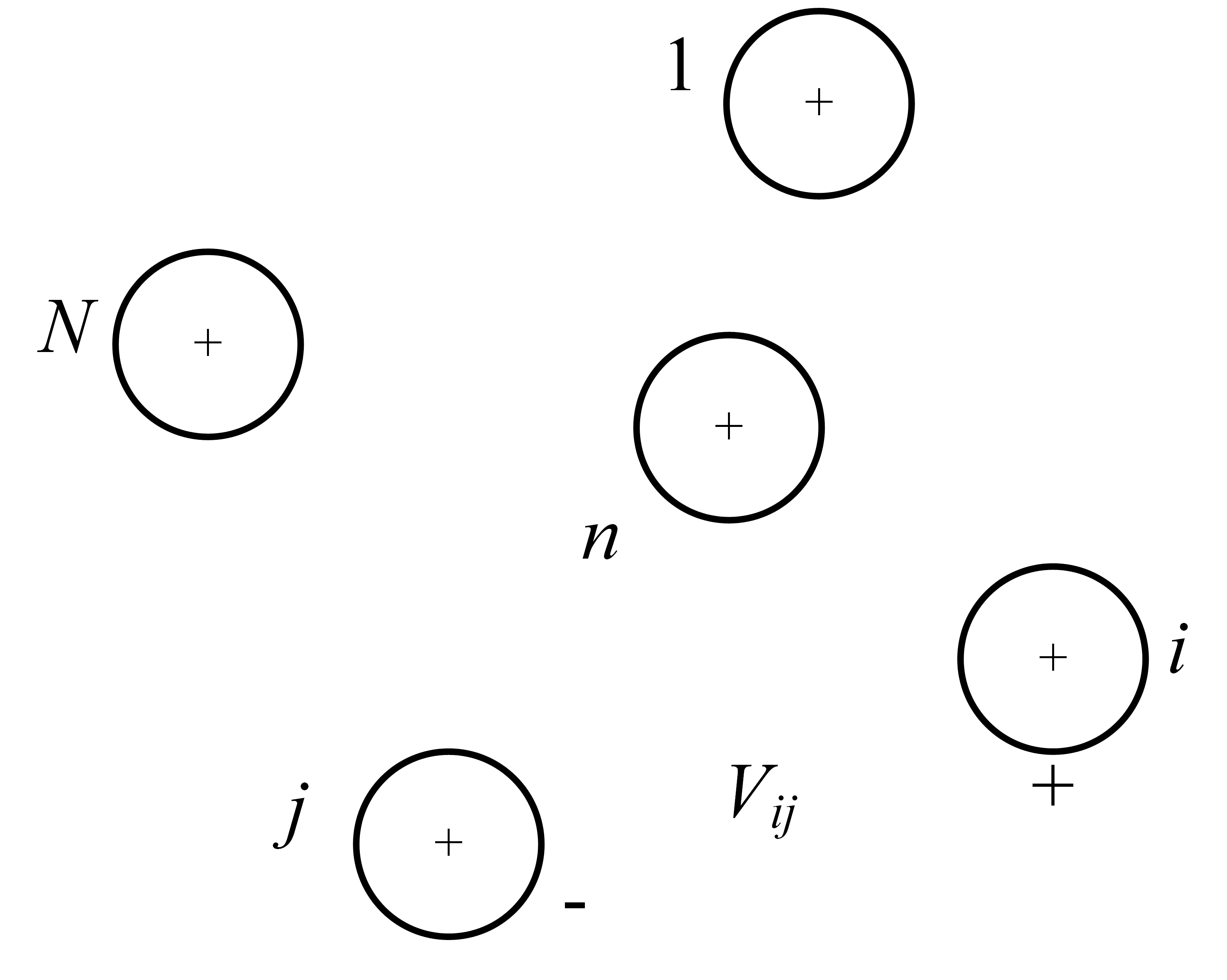 $一组带正电的实心圆导体\label{p5.2}$

可以写成一般形式：

\[\begin{equation} V_{ij} = \frac{1}{2\pi \varepsilon }\sum_{n=1}^{N}q_n\ln\frac{D_{nj}}{D_{ni}} \label{5.2} \end{equation}\]

式中：

$\varepsilon =\varepsilon_0 \varepsilon_\text{r}$，为介质的介电常数；

$\varepsilon_0 = 8.85\times 10^{-12}$ F/m，为真空的介电常数；

$\varepsilon_\text{r}$为介质的相对介电常数；

$q_n$为导体$n$上的电荷密度（C/m）；

$D_{ni}$为导体$n$和导体$i$之间的距离（m）；

$D_{nj}$为导体$n$和导体$j$之间的距离（m）；

$RD_n$为导体$n$的半径。

架空线的并联导纳

架空线路的并联电容计算采用镜像法。这与在第1节中Carson方程的一般应用中使用的方法相同。图示意了导体及其镜像，将用于推导架空线路的一般压降公式。

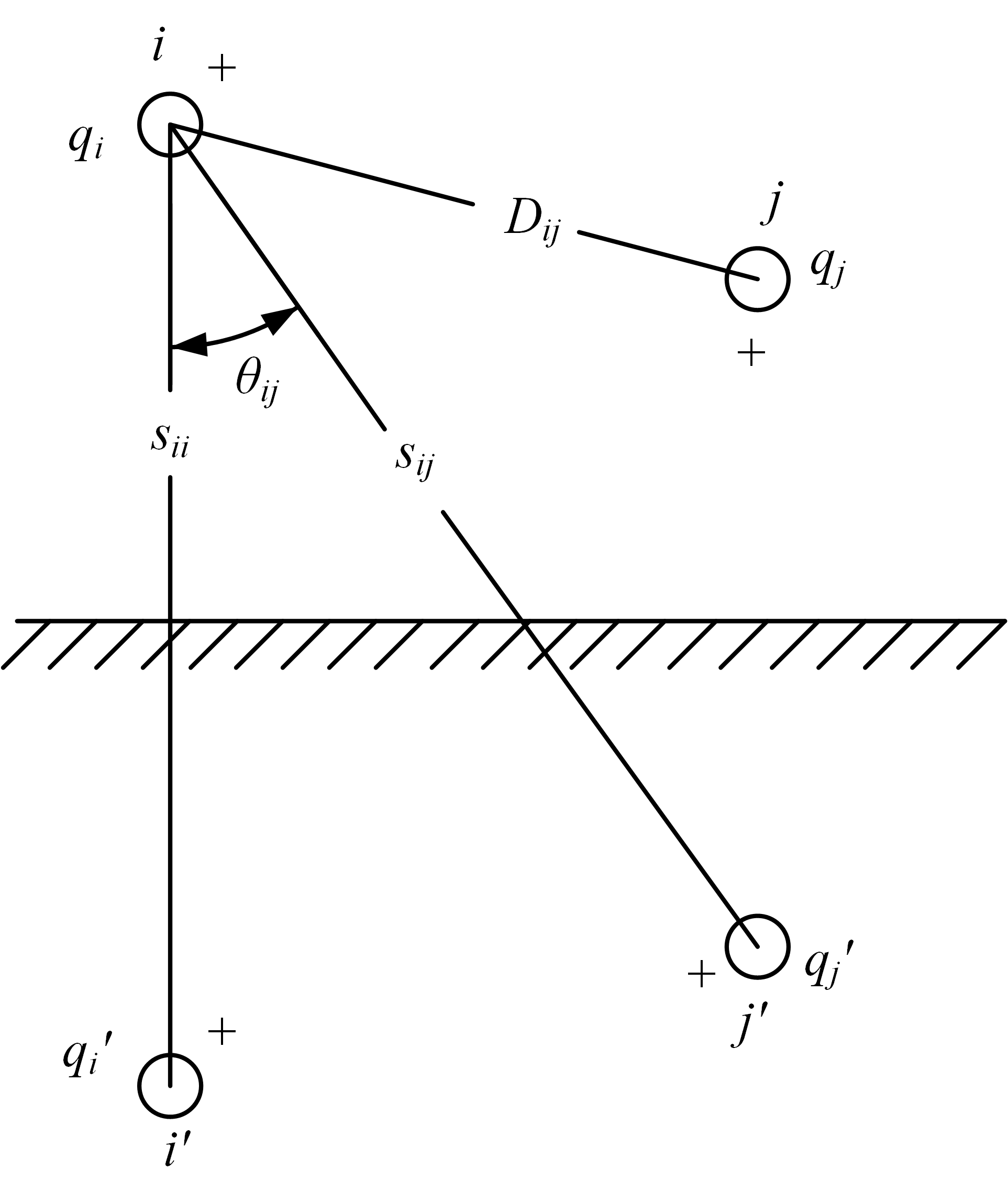
$导体及其镜像\label{p5_3}$

在图中假定:

\[\begin{equation} q_i^{'} = -q_i \quad \text{且} \quad q_j^{'}=-q_j \label{5.3} \end{equation}\]

将电压降方程应用于上图，得

\[\begin{equation} V_{ii^{'}} = \frac{1}{2\pi \varepsilon }\left(q_i\ln\frac{S_{ii}}{RD_i}+q_i^{'}\ln\frac{RD_i}{S_{ii}}+q_j\ln\frac{S_{ij}}{D_{ij}}+q_j^{'}\ln\frac{D_{ij}}{S_{ij}}\right) \label{5.4} \end{equation}\]

简化为

\[\begin{align} V_{ii^{'}} & = \frac{1}{2\pi \varepsilon }\left(q_i\ln\frac{S_{ii}}{RD_i}-q_i\ln\frac{RD_i}{S_{ii}}+q_j\ln\frac{S_{ij}}{D_{ij}}-q_j\ln\frac{D_{ij}}{S_{ij}}\right) \nonumber \\ ~ & = \frac{1}{2\pi \varepsilon }\left(q_i\ln\frac{S_{ii}}{RD_i}+q_i\ln\frac{S_{ii}}{RD_i}+q_j\ln\frac{S_{ij}}{D_{ij}}+q_j\ln\frac{S_{ij}}{D_{ij}}\right) \label{5.5}\\ ~ & = \frac{1}{2\pi \varepsilon }\left(2 q_i\ln\frac{S_{ii}}{RD_i}+2 q_j\ln\frac{S_{ij}}{D_{ij}}\right) \nonumber \end{align}\]

式中：

$S_{ii}$为从导体$i$到其镜像$i^{'}$的距离(m)；

$S_{ij}$为从导体$i$到导体$j$的镜像$j^{'}$的距离(m)；

$D_{ij}$为从导体$i$到导体$j$的距离(m)；

$RD_i$为导体$i$的半径(m)。

上式给出导体$i$与其镜像$i^{'}$之间的总电压降，导体$i$和地之间的电压降是其一半：

\[\begin{equation} V_{ig} = \frac{1}{2\pi \varepsilon }\left(q_i\ln\frac{S_{ii}}{RD_i}+q_j\ln\frac{S_{ij}}{D_{ij}} \right ) \label{5.6} \end{equation}\]

写成一般形式：

\[\begin{equation} V_{ig} = \hat{P}_{ii}\cdot q_i+\hat{P}_{ij}\cdot q_j \label{5.7} \end{equation}\]

式中：$\hat{P}_{ii}$和$\hat{P}_{ij}$是自电位系数和互电位系数。

对于架空线，空气的相对介电常数设为1.0，因此：

\[\begin{align} \label{5.8} \begin{split} \varepsilon _{\mbox{air}} = 1.0\times 8.85\times 10^{-12} \ \text{F/m} = 8.85 \times 10^{-3} \ \mu \text{F/km} \end{split} \end{align}\]

使用以$\mu \text{F/km}$为单位的介电常数值，自电位系数和互电位系数定义为

\[\begin{align} \hat{P}_{ii} & = 17.9836 \ln\frac{S_{ii}}{RD_i} \ \text{(km/}\mu \text{F)} \label{5.9} \\ \hat{P}_{ij} & = 17.9836 \ln\frac{S_{ij}}{D_{ij}} \ \text{(km/}\mu \text{F)} \label{5.10} \end{align}\]

在应用以上公式时，$RD_i$、$S_{ii}$、$S_{ij}$和$D_{ij}$的单位必须相同。对于架空线，导体之间的距离通常以m为单位，由表查得的导体直径通常以cm为单位。必须注意确保在应用两个公式时使用以m为单位的半径。

对于$n$相线组成的架空线，可以构造$n$行$n$列的原始电位系数矩阵[$\hat{p}_{\text{primitive}}$]。对于四线接地的星形线，原始电位系数矩阵为

\[\begin{equation} [\hat{p}_{\text{primitive}}] = \begin{bmatrix} \hat{p}_{aa} & \hat{p}_{ab} & \hat{p}_{ac} & \cdots & \hat{p}_{an}\\ \hat{p}_{ba} & \hat{p}_{bb} & \hat{p}_{bc} & \cdots & \hat{p}_{bn}\\ \hat{p}_{ca} & \hat{p}_{cb} & \hat{p}_{cc} & \cdots & \hat{p}_{cn}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \hat{p}_{na} & \hat{p}_{nb} & \hat{p}_{nc} & \cdots &\hat{p}_{nn} \end{bmatrix} \label{5.11} \end{equation}\]

式中的点划分了矩阵的第三行和第四行、第三列和第四列。分块形式为

\[\begin{equation} [\hat{p}_{\text{primitive}}] = \begin{bmatrix} [\hat{p}_{ij}] & [\hat{p}_{in}]\\ [\hat{p}_{nj}] & [\hat{p}_{nn}] \end{bmatrix} \label{5.12} \end{equation}\]

因为中性线是接地的，所以可以使用克朗还原法将矩阵化简为$n$×$n$的相电位系数矩阵[$P_{abc}$]：

\[\begin{equation} [P_{abc}]=[\hat{P}_{ij}]-[\hat{P}_{in}]\cdot [\hat{P}_{nn}]^{-1}\cdot [\hat{P}_{nj}] \label{5.13} \end{equation}\]

电位系数矩阵的逆是$n \times n$电容矩阵[$C_{abc}$]：

\[\begin{equation} [C_{abc}]=[P_{abc}]^{-1} \label{5.14} \end{equation}\]

对于两相线，电容矩阵大小为2×2，这就必须为缺失的相插入一个零行和零列。对于单相线路，电容矩阵将得到单个元素，同样必须为缺失的相插入零行和零列。在单相线路的情况下，唯一的非零项是使用中的那一相。

忽略并联电导，相并联导纳矩阵由下式给出：

\[\begin{equation} [y_{abc}] =0+\text{j} \omega [C_{abc}] \ \text{(}\mu \text{S/km)} \label{5.15} \end{equation}\]

式中：$\omega = 2\pi f=314.1593$。

例题四

计算例2.1中架空线的并联导纳矩阵。

例2.1：一条架空三相配电线的构造如图所示。计算相线阻抗矩阵和线路的正序和零序阻抗。相线导体型号为336,400 26/7 钢芯铝绞线，中性线导体型号为4/0 6/1 钢芯铝绞线。

$架空三相配电线\label{p4.7}$

解答

假设中性线距离地面7.6220m。导体表（附录A）中相线和中性线的直径为

导体： 336,400 26/7 $\quad$ 钢芯铝绞线: $d_\text{c}$ = 1.83134 cm, $RD_\text{c}$= 0.009157 m

$\qquad$ $\quad$ 4/0 6/1 $\quad$ 钢芯铝绞线: $d_\text{s}$ = 1.43002 cm, $RD_\text{s}$ = 0.007150 m

对于这个结构，矩阵形式的导体和镜像之间的距离为

\[ [S]=\begin{bmatrix} 17.683 & 17.6994 & 17.8113 & 16.5086\\ 17.6994 & 17.683 & 17.7361 & 16.4699\\ 17.8113 & 17.7361 & 17.683 & 16.4889\\ 16.5086 & 16.4699 & 16.4889 & 15.244 \end{bmatrix} \ \text{(m)} \]

$a$相的自原始电位系数和$a$相与$b$相之间的互原始电位系数为

\[\begin{gather*} \hat{P}_{aa} = 17.9836\times \ln\frac{17.683}{0.009157}=136.0610\ \text{(km/μF)}\\ \hat{P}_{ab} = 17.9836\times \ln\frac{17.6994}{0.7622}=56.5598\ \text{(km/μF)} \end{gather*}\]

总原始电位系数矩阵的计算结果为

\[ [\hat{P}_{\text{primitive}}] = \begin{bmatrix} 136.0610 & 56.5598 & 38.1565 & 40.6219\\ 56.5598 & 136.0610 & 46.0260 & 45.6667\\ 38.1565 & 46.0260 & 136.0610 & 42.8205\\ 40.6219 & 45.6667 & 42.8205 & 137.8412 \end{bmatrix} \ \text{(km/}\mu \text{F)} \]

由于第四条线（中性线）接地，因此可以使用克朗还原法来计算相电位系数矩阵，[$\hat{P}_{44}$]项是单个元素，因此可以将此情况下的克朗还原公式修正为

\[ P_{ij}=\hat{P}_{ij}-\frac{\hat{P}_{i4} \hat{P}_{4j}}{\hat{P}_{44}} \]

式中：$i = 1,2,3$，$j = 1,2,3$。

例如，$P_{cb}$值的计算结果为

\[ P_{cb}=\hat{P}_{3,2}-\frac{\hat{P}_{3,4} \hat{P}_{4,2}}{\hat{P}_{4,4}}=31.8396 \ \text{(km/}\mu \text{F)} \]

克朗还原后，相电位系数矩阵是：

\[ [P_{abc}]=\begin{bmatrix} 124.0897 & 43.1018 & 25.5373\\ 43.1018 & 120.9317 & 31.8396\\ 25.5373 & 31.8396 & 122.7588 \end{bmatrix} \ \text{(km/}\mu \text{F)} \]

对$[P_{abc}]$求逆得到并联电容矩阵$[C_{abc}]$：

\[ [C_{abc}]=[P_{abc}]^{-1}=\begin{bmatrix} 0.0093 & -0.0030 & -0.0012\\ -0.0030 & 0.0099 & -0.0019\\ -0.0012 & -0.0019 & 0.0089 \end{bmatrix} \ \text{(}\mu \text{F/km)} \]

用角频率乘以[$C_{abc}$]计算得到最终的三相并联导纳矩阵：

\[ [y_{abc}]=\text{j}\omega [C_{abc}]=\begin{bmatrix} \text{j}2.9370 & -\text{j}0.9508 & -\text{j}0.3644\\ -\text{j}0.9508 & \text{j}3.0961 & -\text{j}0.6052\\ -\text{j}0.3644 & -\text{j}0.6052 & \text{j}2.7919 \end{bmatrix} \ \text{(}\mu \text{S/km)} \]

同轴中性电缆的并联导纳

大多数地下配电线由一根或多根同轴中性电缆组成。

图所示是一个基本同轴中性电缆，中心导体（黑色）是相导体，同轴中性线（灰色）绕半径为$R_\text{b}$的圆周均匀分布。参考图有定义如下：

$R_\text{b}$ 穿过中性线中心的圆的半径
$d_\text{c}$ 相导体的直径
$d_\text{s}$ 中性线的直径
$k$ 中性线的数量

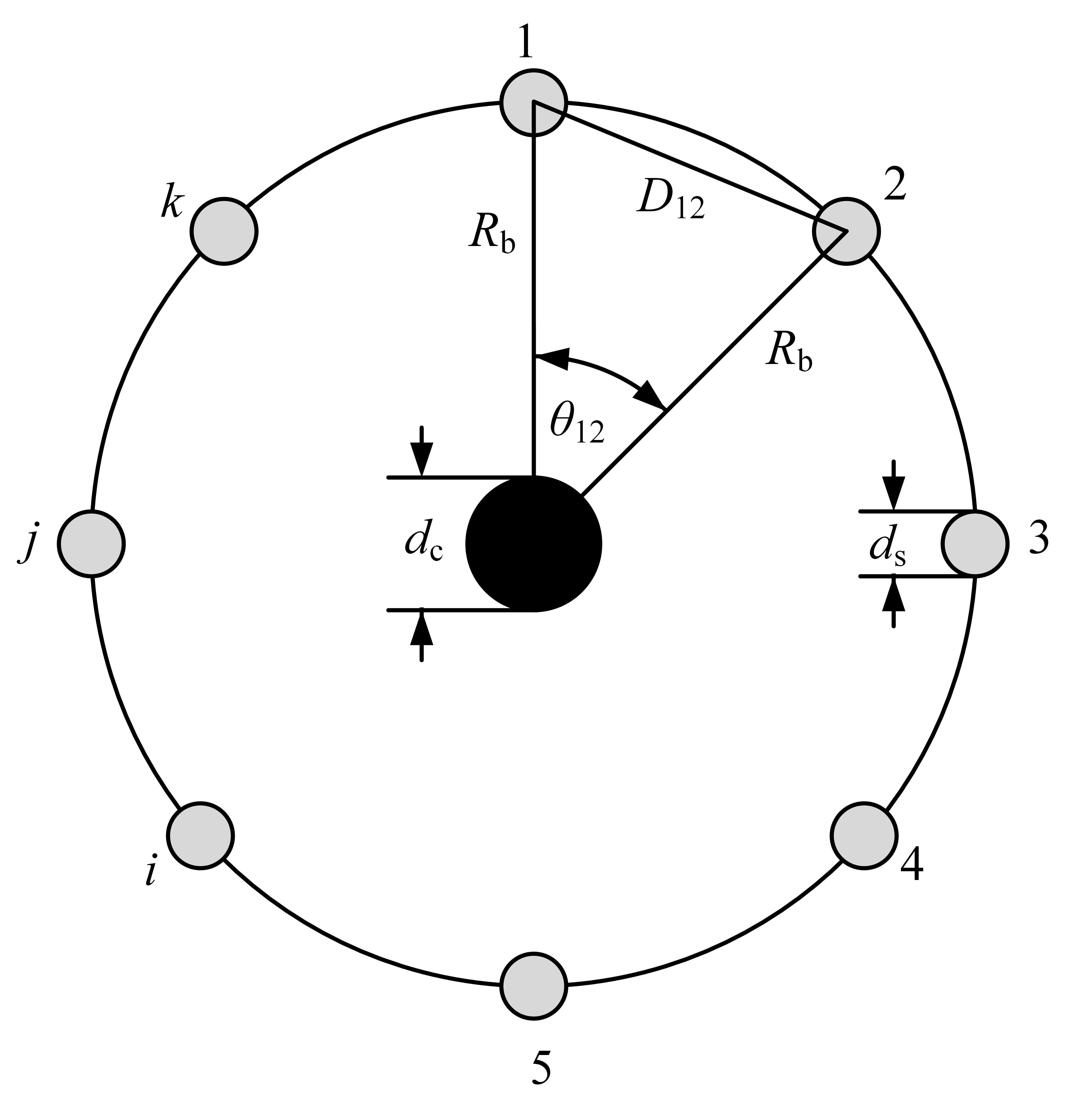
$基本同轴中性电缆\label{p5.4}$

同轴中性线接地，因此它们电位相同，可假设相导体上的电荷产生的电场被限制在同轴中性线的边界上。为了计算相导体和地之间的电容，可以使用一般电压降公式。由于所有中性线电位相同，因此只需要确定相导线$p$和中性线1之间的电位差。

\[\begin{equation} V_{p1}=\frac{1}{2\pi \varepsilon }\left(q_p\ln\frac{R_\text{b}}{RD_\text{c}}+q_1\ln\frac{RD_\text{s}}{R_\text{b}}+q_2\ln\frac{D_{12}}{R_\text{b}}+\cdots +q_i\ln\frac{D_{1i}}{R_\text{b}}+\cdots +q_k\ln\frac{D_{1k}}{R_\text{b}} \right ) \label{5.16} \end{equation}\]

式中：$RD_\text{c} =\displaystyle\frac{d_\text{c}}{2}$，$RD_\text{s} = \displaystyle\frac{d_\text{s}}{2}$。

假定每条中性线带有相同的电荷，使得

\[\begin{equation} q_1=q_2=q_i=q_k=-\frac{q_p}{k} \label{5.17} \end{equation}\]

上式简化为

\[\begin{align} \label{5.18} \begin{split} V_{p1} & = \frac{1}{2\pi \varepsilon }\left[q_p\ln\frac{R_\text{b}}{RD_\text{c}}-\frac{q_p}{k}\left(\ln\frac{RD_\text{s}}{R_\text{b}}+\ln\frac{D_{12}}{R_\text{b}}+\cdots +\ln\frac{D_{1i}}{R_\text{b}}+\cdots +\ln\frac{D_{1k}}{R_\text{b}} \right )\right] \\ ~ & = \frac{q_p}{2\pi \varepsilon }\left[\ln\frac{R_\text{b}}{RD_\text{c}}-\frac{1}{k}\left(\ln\frac{RD_\text{s}\cdot D_{12}\cdot D_{1i}\cdot \ \cdots \ \cdot D_{1k}}{R_\text{b}^{k}} \right )\right] \end{split} \end{align}\]

式中第二个ln项的分子表示中性线$i$和所有其他中性线之间的距离和半径的乘积。参照图，有下列关系成立：

\[\begin{align} \theta _{12} & =\frac{2 \pi }{k} \nonumber \\ \theta _{13} & =2 \theta _{12}=\frac{4 \pi }{k} \nonumber \end{align}\]

中性线1与任意其他中性线$i$之间的夹角由下式给出：

\[\begin{equation} \theta _{1i}=(i-1)\theta _{12}=\frac{2(i-1) \pi }{k} \label{5.19} \end{equation}\]

不同中性线之间的距离由下式给出：

\[\begin{gather*} D_{12}=2 R_\text{b} \sin\left(\frac{\theta _{12}}{2}\right)=2 R_\text{b} \sin\left(\frac{\pi }{k}\right)\\ D_{13}=2 R_\text{b} \sin\left(\frac{\theta _{13}}{2}\right)=2 R_\text{b} \sin\left(\frac{2\pi }{k}\right) \end{gather*}\]

中性线1与任何其他中性线$i$之间的距离由下式给出：

\[\begin{equation} D_{1i}=2 R_\text{b} \sin\left(\frac{\theta _{1i}}{2}\right)=2 R_\text{b} \sin\left(\frac{(i-1)\pi }{k}\right) \label{5.20} \end{equation}\]

上式可用于展开$V_{p1}$式的第二个ln项的分子：

\[\begin{eqnarray} \label{5.21} &&RD_\text{s}\cdot D_{12}\cdot \ \cdots \ \cdot D_{1i}\cdot \ \cdots \ \cdot D_{1k} \notag \\ &&\qquad \quad = RD_\text{s} R_\text{b}^{k-1}\left[2\sin\left(\frac{\pi }{k}\right )\cdot \ \cdots\ \cdot2\sin\left(\frac{(i-1)\pi }{k} \right )\cdot \ \cdots\ \cdot2\sin\left(\frac{(k-1)\pi }{k} \right ) \right ] \end{eqnarray}\]

式中方括号内的项是一个三角恒等式，仅等于股数$k$。应用这个等式，$V_{p1}$式变为

\[\begin{align} \label{5.22} \begin{split} V_{p1} & = \frac{q_p}{2\pi \varepsilon }\left[\ln\frac{R_\text{b}}{RD_\text{c}}-\frac{1}{k}\left(\ln\frac{k\cdot RD_\text{s}\cdot R_\text{b}^{k-1}}{R_\text{b}^{k}} \right ) \right ] \\ ~ & = \frac{q_p}{2\pi \varepsilon }\left[\ln\frac{R_\text{b}}{RD_\text{c}}-\frac{1}{k}\left(\ln\frac{k\cdot RD_\text{s}}{R_\text{b}} \right ) \right ] \end{split} \end{align}\]

该式给出了从相导体到中性线1的电压降。通常，地下间距以m为单位，因此相导体的半径（$RD_\text{c}$）和中性线导体的半径（$RD_\text{s}$）应以m为单位。由于中性线均接地，因此该式同时也给出了相导体与地之间的电压降。鉴于此，同轴中性电缆相到地的电容由下式给出：

\[\begin{equation} \label{5.23} C_{pg} = \frac{q_P}{V_{p1}} = \displaystyle\frac{2\pi \varepsilon }{\ln\displaystyle\frac{R_\text{b}}{RD_\text{c}}-\displaystyle\frac{1}{k}\ln\displaystyle\frac{k\cdot RD_\text{s}}{R_\text{b}}} \end{equation}\]

式中：$\varepsilon=\varepsilon _0 \varepsilon _\text{r}$为介质的介电常数；$\varepsilon _0$为自由空间的介电常数，其值为$8.85\times 10^{-12}$ F/m；$\varepsilon _\text{r}$为介质的相对介电常数。

电缆的电场被限制在绝缘材料上，绝缘材料的相对介电常数都有一个取值范围。表给出了四种常用绝缘材料的相对介电常数。交联聚乙烯是一种非常受欢迎的绝缘材料，如果假定取其相对介电常数的最小值2.3，则同轴中性电缆的并联导纳方程为

\[\begin{equation} \label{5.24} y_{ag} = 0+\text{j}\displaystyle\frac{40.1792}{\ln\displaystyle\frac{R_\text{b}}{RD_\text{c}}-\displaystyle\frac{1}{k}\ln\displaystyle\frac{k\cdot RD_\text{s}}{R_\text{b}}}\ \text{(}\mu \text{S/km)} \end{equation}\]

材料	相对介电常数取值范围
聚氯乙烯(PVC)	3.4-8.0
乙烯-丙烯橡胶(EPR)	2.5-3.5
聚乙烯(PE)	2.5-2.6
交联聚乙烯(XLPE)	2.3-6.0

例题五

计算例2.2的同轴中性线的三相并联导纳矩阵。

例2.2：三个同轴中性电缆埋在沟槽中，如图所示。电缆为电压等级为15 kV，相导体型号为250000 CON LAY 铝合金，中性线为13股14号退火涂层铜线（1/3中性）。中性线上的电缆外径$d_\text{od}$为3.2766 cm（附录B）。计算相阻抗矩阵和序阻抗矩阵。

$三相同轴中性电缆\label{p4.11}$

解答

由例2.2得

\[ R_\text{b} = R =0.01557\ \text{m} = 1.557\ \text{cm} \]

250000铝合金相导体的直径为1.4402 cm：

\[ RD_\text{c} = \frac{1.4402}{2} = 0.7201\ \text{(cm)} \]

14号铜同轴中性线的直径为0.1628 cm：

\[ RD_\text{s} = \frac{0.1628}{2} = 0.0814\ \text{(cm)} \]

代入式中计算得：

\[ y_{ag} = \text{j}\displaystyle\frac{40.1792}{\ln\displaystyle\frac{R_\text{b}}{RD_\text{c}}-\displaystyle\frac{1}{k}\ln\displaystyle\frac{k\cdot RD_\text{s}}{R_\text{b}}} =\text{j}50.172\ \text{(}\mu \text{S/km)} \]

该三相地下线路的相导纳矩阵为

\[ [y_{abc}] = \begin{bmatrix} \text{j}50.172 & 0 & 0\\ 0 & \text{j}50.172 & 0\\ 0 & 0 & \text{j}50.172 \end{bmatrix} \ \text{(}\mu \text{S/km)} \]

带屏蔽电缆地下线的并联导纳

下图为一带屏蔽电缆示意图。$R_\text{b}$是通过屏蔽带中心的圆的半径。与同轴中性电缆一样，电场被限制在绝缘层中，因此前表的相对介电常数同样适用。

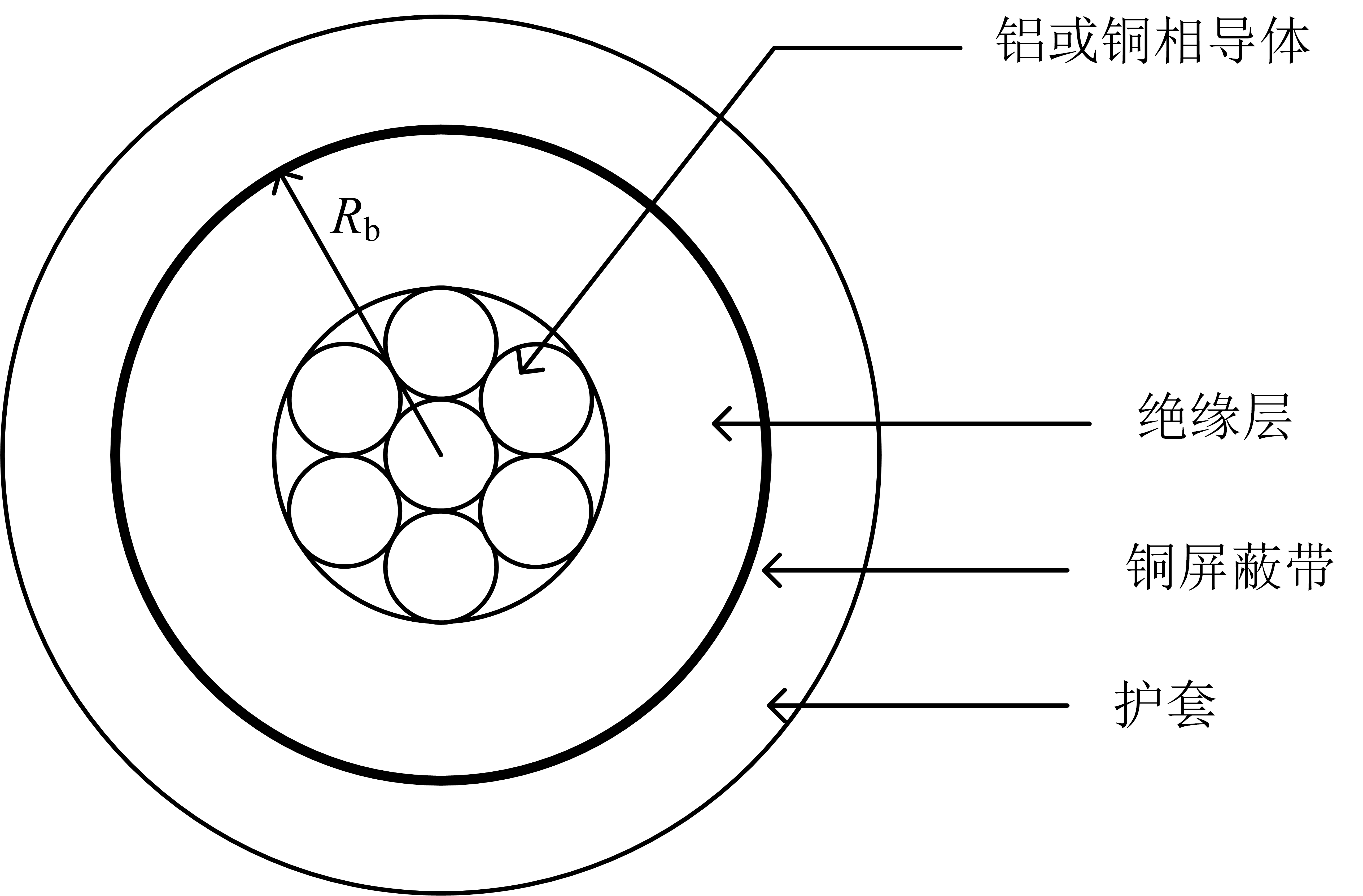
$带屏蔽电缆\label{p5.5}$

屏蔽带导体可以看作是同轴中性电缆，其中股线$k$的数量变得无限大。因此，屏蔽带导体的并联导纳方程变为

\[\begin{equation} y_{ag} = 0+\text{j}\displaystyle\frac{40.1792}{\ln\displaystyle\frac{R_\text{b}}{RD_\text{c}}} \ \text{(}\mu \text{S/km)} \label{5.25} \end{equation}\]

例题六

计算第1节中例2.3的单相带屏蔽电缆的并联导纳。

例2.3：单相电路由1/0 铝合金绝缘带屏蔽电缆和1/0 铜中性导体组成，如图所示，单相线连接到$b$相。计算相阻抗矩阵，假设$\rho$ = 2.3715×10$^{-8}$ $\Omega\cdot$m。

$带中性线的单相带屏蔽电缆\label{p4.13}$

解答

从例2.3中可得，屏蔽层外径$d_\text{s}$为2.2352 cm，屏蔽层厚度$T$为130 $\mu \text{m}$。穿过屏蔽带中心的圆的半径是：

\[ R_\text{b} = \displaystyle\frac{d_\text{s}-\displaystyle\frac{T}{10000}}{2} = 1.1111 \ \text{(cm)} \]

1/0 铝合金相导体的直径为0.9347 cm。

\[ RD_\text{c} = \frac{0.9347}{2} = 0.4674\ \text{(cm)} \]

\[ y_{bg} = \text{j}\displaystyle\frac{40.1792}{\ln \left(\displaystyle\frac{R_\text{b}}{RD_\text{c}} \right )}=\text{j}46.401\ \text{(}\mu \text{S/km)} \]

该线在$b$相上，相导纳矩阵变为

\[ [y_{abc}] = \begin{bmatrix} 0 & 0 & 0\\ 0 & \text{j}46.401 & 0\\ 0 & 0 & 0 \end{bmatrix} \ \text{(}\mu \text{S/km)} \]

序导纳

三相线的序导纳可以按照与确定序阻抗大致相同的方式确定。假设3 $\times$ 3导纳矩阵以S/km为单位。则作为线对地电压的函数的三相电容电流由下式给出：

\[\begin{gather} \begin{bmatrix} I_{\text{cap}a}\\ I_{\text{cap}b}\\ I_{\text{cap}c} \end{bmatrix} = \begin{bmatrix} y_{aa} & y_{ab} & y_{ac}\\ y_{ba} & y_{bb} & y_{bc}\\ y_{ca} & y_{cb} & y_{cc} \end{bmatrix} \cdot \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix} \label{5.26}\\ [I_{\text{cap}abc}] = [y_{abc}]\cdot [VLG_{abc}] \label{5.27} \end{gather}\]

应用对称分量变换：

\[\begin{equation} [I_{\text{cap}012}] = [A_\text{s}]^{-1}\cdot [I_{\text{cap}abc}] = [A_\text{s}]^{-1}\cdot [y_{abc}]\cdot [A_\text{s}]\cdot [VLG_{012}] \label{25.28} \end{equation}\]

序导纳矩阵：

\[\begin{equation} [y_{012}] = [A_\text{s}]^{-1}\cdot [y_{abc}]\cdot [A_\text{s}] =\begin{bmatrix} y_{00} & y_{01} & y_{02}\\ y_{10} & y_{11} & y_{12}\\ y_{20} & y_{21} & y_{22} \end{bmatrix} \label{5.29} \end{equation}\]

对于不对称间距的三相架空线路，其序导纳矩阵是满秩的，即非对角线项是非零的。然而，由于相间没有互电容，因此具有三条相同电缆的三相地下线路将仅具有对角线项。实际上，序导纳和相导纳完全相同。

配电网络线路模型

架空线和地下线的建模是配电馈线分析的关键步骤，考虑线路的实际相位和导线之间的正确间距非常重要。前面介绍了计算相阻抗矩阵和相位导纳矩阵的方法，这些矩阵将用于架空线路和地下线路的模型。

精确线路段模型

三相、两相或单相架空线路和地下线路的三相线路段精确模型如图所示。

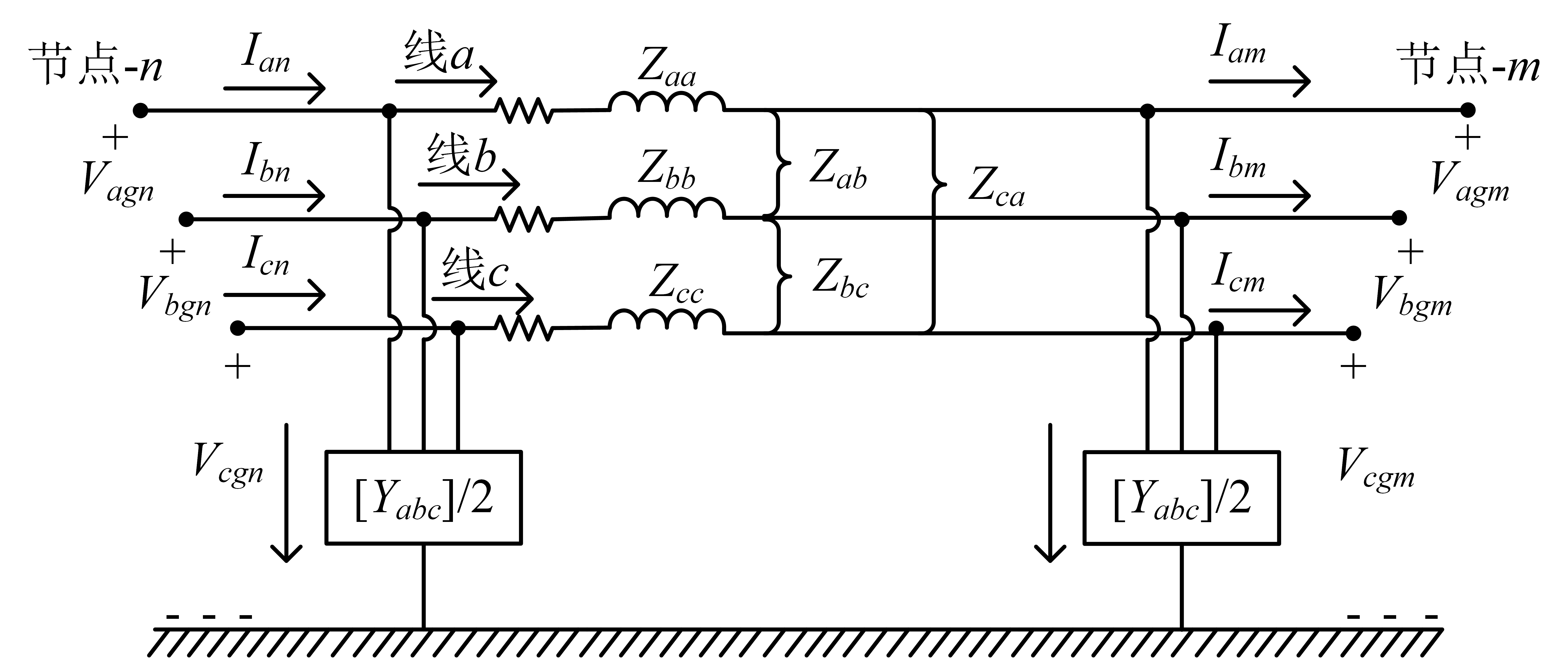
$三相线路段精确模型\label{p6.1}$

在所有情况下，相阻抗和相导纳矩阵大小均为3 $\times$ 3（两相或单相线路中缺少的相用零来填补），因此可以使用一套方程来描述所有架空线和地下线路段。图中的阻抗和导纳值表示线路的总阻抗和总导纳。即相阻抗矩阵和相导纳矩阵均已乘以线路的长度。

对于上图的线路段，描述输入（节点$n$）的电压和电流与输出（节点$m$）的电压和电流关系的方程如下。

在节点$m$处应用基尔霍夫电流定律：

\[\begin{equation} \begin{bmatrix} I_{\text{line}a}\\ I_{\text{line}b}\\ I_{\text{line}c} \end{bmatrix}_n = \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_m +\frac{1}{2} \begin{bmatrix} Y_{aa} & Y_{ab} & Y_{ac}\\ Y_{ba} & Y_{bb} & Y_{bc}\\ Y_{ca} & Y_{cb} & Y_{cc} \end{bmatrix} \cdot \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_m \label{6.1} \end{equation}\]

在矩阵形式中，上式变为

\[\begin{equation} [I_{\text{line}abc}]_n = [I_{abc}]_m +\frac{1}{2}[Y_{abc}]\cdot [VLG_{abc}]_m \label{6.2} \end{equation}\]

将基尔霍夫电压定律应用于该模型：

\[\begin{equation} \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_n = \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_m + \begin{bmatrix} Z_{aa} & Z_{ab} & Z_{ac}\\ Z_{ba} & Z_{bb} & Z_{bc}\\ Z_{ca} & Z_{cb} & Z_{cc} \end{bmatrix}\cdot \begin{bmatrix} I_{\text{line}a}\\ I_{\text{line}b}\\ I_{\text{line}c} \end{bmatrix}_m \label{6.3} \end{equation}\]

在矩阵形式中，上式变为

\[\begin{equation} [VLG_{abc}]_n = [VLG_{abc}]_m+[Z_{abc}]\cdot [I_{\text{line}abc}]_m \label{6.4} \end{equation}\]

考虑到$[I_{\text{line}abc}]_n=[I_{\text{line}abc}]_m$，将上两式联立得：

\[\begin{equation} [VLG_{abc}]_n = [VLG_{abc}]_m+[Z_{abc}]\cdot \left\{[I_{abc}]_m + \frac{1}{2} [Y_{abc}] \cdot [VLG_{abc}]_m \right\} \label{6.5} \end{equation}\]

整理得到：

\[\begin{equation} [VLG_{abc}]_n = \left \{[U]+\frac{1}{2}\cdot [Z_{abc}]\cdot [Y_{abc}] \right\}\cdot [VLG_{abc}]_m+[Z_{abc}]\cdot [I_{abc}]_m \label{6.6} \end{equation}\]

其中：

\[\begin{equation} [U] = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \label{6.7} \end{equation}\]

式简写为

\[\begin{equation} [VLG_{abc}]_n = [a]\cdot [VLG_{abc}]_m+[b]\cdot [I_{abc}]_m \label{6.8} \end{equation}\]

其中：

$[a] = [U]+\frac{1}{2}\cdot [Z_{abc}]\cdot [Y_{abc}] \label{6.9}$ $\quad$ $[b] = [Z_{abc}] \label{6.10}$

节点$n$处线路段的输入电流为

\[\begin{equation} \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_n = \begin{bmatrix} I_{\text{line}a}\\ I_{\text{line}b}\\ I_{\text{line}c} \end{bmatrix}_m +\frac{1}{2}\cdot \begin{bmatrix} Y_{aa} & Y_{ab} & Y_{ac}\\ Y_{ba} & Y_{bb} & Y_{bc}\\ Y_{ca} & Y_{cb} & Y_{cc} \end{bmatrix}\cdot \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_n \label{6.11} \end{equation}\]

变为

\[\begin{equation} [I_{abc}]_n = [I_{\text{line}abc}]_m + \frac{1}{2}\cdot [Y_{abc}]\cdot [VLG_{abc}]_n \label{6.12} \end{equation}\]

考虑到$[I_{\text{line}abc}]_n=[I_{\text{line}abc}]_m$，将$[I_{\text{line}abc}]_n$式代入上式:

\[\begin{equation} [I_{abc}]_n = [I_{abc}]_m + \frac{1}{2}\cdot [Y_{abc}]\cdot [VLG_{abc}]_m + \frac{1}{2}\cdot [Y_{abc}]\cdot [VLG_{abc}]_n \label{6.13} \end{equation}\]

将$[VLG_{abc}]_n$式代入上式:

\[\begin{multline} [I_{abc}]_n = [I_{abc}]_m + \frac{1}{2}\cdot [Y_{abc}]\cdot [VLG_{abc}]_m + \frac{1}{2}\cdot [Y_{abc}]\\ \times \left(\left \{[U]+\frac{1}{2}\cdot [Z_{abc}]\cdot [Y_{abc}] \right\}\cdot [VLG_{abc}]_m+[Z_{abc}]\cdot [I_{abc}]_m \right ) \label{6.14} \end{multline}\]

整理得到：

\[\begin{eqnarray} &&[I_{abc}]_n = \left\{[Y_{abc}]+\frac{1}{4}\cdot [Y_{abc}]\cdot [Z_{abc}]\cdot [Y_{abc}] \right\} \cdot [VLG_{abc}]_m \notag \\ && \qquad \qquad + \left \{[U]+\frac{1}{2}\cdot [Y_{abc}]\cdot [Z_{abc}]\right \}[I_{abc}]_m \label{6.15} \end{eqnarray}\]

简写为

\[\begin{equation} [I_{abc}]_n = [c] \cdot [VLG_{abc}]_m + [d]\cdot [I_{abc}]_m \label{6.16} \end{equation}\]

其中：

\[\begin{gather} [c] = [Y_{abc}]+\frac{1}{4}\cdot [Y_{abc}]\cdot [Z_{abc}]\cdot [Y_{abc}] \label{6.17}\\ [d] = [U]+\frac{1}{2}\cdot [Z_{abc}]\cdot [Y_{abc}] \label{6.18} \end{gather}\]

写为分块矩阵形式：

\[\begin{equation} \begin{bmatrix} [VLG_{abc}]_n\\ [I_{abc}]_n \end{bmatrix} = \begin{bmatrix} [a] & [b]\\ [c] & [d] \end{bmatrix} \cdot \begin{bmatrix} [VLG_{abc}]_m\\ [I_{abc}]_m \end{bmatrix} \label{6.19} \end{equation}\]

当定义了$a$、$b$、$c$、$d$参数时，上式与输电线分析中使用的公式非常相似。这里$a$、$b$、$c$、$d$参数是3 $\times$ 3矩阵而不是单个变量，并且被称为广义矩阵。根据节点$n$处的电压和电流，同样可以由上述公式来计算节点$m$处的电压和电流：

\[\begin{equation} \begin{bmatrix} [VLG_{abc}]_m\\ [I_{abc}]_m \end{bmatrix} = \begin{bmatrix} [a] & [b]\\ [c] & [d] \end{bmatrix}^{-1} \cdot \begin{bmatrix} [VLG_{abc}]_n\\ [I_{abc}]_n \end{bmatrix} \label{6.20} \end{equation}\]

$a$、$b$、$c$、$d$矩阵的逆矩阵可以简单地求出，因为存在以下关系：

\[\begin{equation} [a]\cdot [d]-[b]\cdot [c]=[U] \label{6.21} \end{equation}\]

由关系前式变为

\[\begin{equation} \begin{bmatrix} [VLG_{abc}]_m\\ [I_{abc}]_m \end{bmatrix} = \begin{bmatrix} [d] & -[b]\\ -[c] & [a] \end{bmatrix} \cdot \begin{bmatrix} [VLG_{abc}]_n\\ [I_{abc}]_n \end{bmatrix} \label{6.22} \end{equation}\]

由于矩阵$[a]$等于矩阵$[d]$，因此上式展开为

\[\begin{align} [VLG_{abc}]_m & = [a]\cdot [VLG_{abc}]_n-[b]\cdot [I_{abc}]_n \label{6.23}\\ [I_{abc}] _m & = -[c]\cdot [VLG_{abc}]_n+[d]\cdot [I_{abc}]_n \label{6.24} \end{align}\]

有时需要根据节点$n$的电压和注入节点$m$的电流来计算节点$m$处的电压，如在第6章介绍的潮流计算迭代方法。

求解母线$m$电压的方程为：

\[\begin{equation} [VLG_{abc}]_m = [a]^{-1}\cdot \{[VLG_{abc}]_n-[b]\cdot [I_{abc}]_m\} \label{6.25} \end{equation}\]

形式为

\[\begin{equation} [VLG_{abc}]_m = [A]\cdot [VLG_{abc}]_n-[B]\cdot [I_{abc}]_m \label{6.26} \end{equation}\]

其中：

\[\begin{gather} [A] = [a]^{-1} \label{6.27}\\ [B] = [a]^{-1}\cdot [b] \label{6.28} \end{gather}\]

因为线路中相线之间的相互耦合程度不相同，所以在每一个相线上都会有不同的电压降值。因此，即使在负荷对称时，配电馈线上的电压也可能不对称。描述不对称程度的一种常用方法是使用美国电气制造商协会（NEMA）定义的式()中的不对称电压：

\[\begin{equation} V_{\text{unbalance}} = \frac{\left | \text{相对于} V_{\text{average}} \text{的最大偏差} \right |}{\left | V_{\text{average}} \right |}\times 100\% \label{6.29} \end{equation}\]

例题七

在10000 m三相线路的节点$m$处有6000 kVA，12.47 kV，0.9滞后功率因数的对称三相负荷。线路段的结构和导体是例2.1的结构和导体。计算广义线常数矩阵$[a]$、$[b]$、$[c]$和$[d]$。使用广义矩阵，计算线路的电源端（节点$N$）上的线对地电压和线电流。

解答

在例2.1和2.4中计算的线路段的相阻抗矩阵和并联导纳矩阵是：

\[\begin{gather*} [z_{abc}]=\begin{bmatrix} 0.2923+\text{j}0.5890 & 0.1051+\text{j}0.2902 & 0.1035+\text{j}0.2301\\ 0.1051+\text{j}0.2902 & 0.2980+\text{j}0.5727 & 0.1064+\text{j}0.2496\\ 0.1035+\text{j}0.2301 & 0.1064+\text{j}0.2496 & 0.2948+\text{j}0.5819 \end{bmatrix}\ \text{(}\Omega \text{/km)}\\ [y_{abc}]=\begin{bmatrix} \text{j}2.9370 & -\text{j}0.9508 & -\text{j}0.3644\\ -\text{j}0.9508 & \text{j}3.0961 & -\text{j}0.6052\\ -\text{j}0.3644 & -\text{j}0.6052 & \text{j}2.7919 \end{bmatrix} \ \text{(}\mu \text{S/km)} \end{gather*}\]

对于10000 m的线路段，总相阻抗矩阵和并联导纳矩阵是：

\[\begin{align} [Z_{abc}] & = \begin{bmatrix} 2.923+\text{j}5.890 & 1.051+\text{j}2.902 & 1.035+\text{j}2.301\\ 1.051+\text{j}2.902 & 2.980+\text{j}5.727 & 1.064+\text{j}2.496\\ 1.035+\text{j}2.301 & 1.064+\text{j}2.496 & 2.948+\text{j}5.819 \end{bmatrix} \ \text{(}\Omega\text{)} \notag \\ [Y_{abc}] & = \begin{bmatrix} \text{j}29.370 & -\text{j}9.508 & -\text{j}3.644\\ -\text{j}9.508 & \text{j}30.961 & -\text{j}6.052\\ -\text{j}3.644 & -\text{j}6.052 & \text{j}27.919 \end{bmatrix} \ \text{(}\mu \text{S)} \notag \end{align}\]

应该注意的是，相线导纳矩阵的元素非常小。因此可认为广义矩阵是：

\[\begin{align} [a] & = [U]+\frac{1}{2}\cdot [Z_{abc}]\cdot [Y_{abc}]=\begin{bmatrix} 1.0 & 0 & 0\\ 0 & 1.0 & 0\\ 0 & 0 & 1.0 \end{bmatrix} \notag \\ [b] & = [Z_{abc}]=\begin{bmatrix} 2.923+\text{j}5.890 & 1.051+\text{j}2.902 & 1.035+\text{j}2.301\\ 1.051+\text{j}2.902 & 2.980+\text{j}5.727 & 1.064+\text{j}2.496\\ 1.035+\text{j}2.301 & 1.064+\text{j}2.496 & 2.948+\text{j}5.819 \end{bmatrix} \notag \\ [c] & =\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} \notag \\ [d] & = \begin{bmatrix} 1.0 & 0 & 0\\ 0 & 1.0 & 0\\ 0 & 0 & 1.0 \end{bmatrix} \end{align}\]

由于相线导纳矩阵的元素太小，所以$[a]$和$[d]$矩阵看起来是单位矩阵。而对于大多数实际应用，因为数量级的缘故，相导纳矩阵可以被忽略。

负荷处线路对地电压的大小为

\[ VLG = \frac{12470}{\sqrt{3}} = 7199.56 \ \text{(V)} \]

选择$A$相对地电压作为参考，负荷的线对地电压矩阵为

\[ \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_m = \begin{bmatrix} 7199.56\angle0\\ 7199.56\angle-120\\ 7199.56\angle120 \end{bmatrix} \ \text{(V)} \]

负荷电流的大小是：

\[ [I]_m = \frac{6000}{\sqrt{3}\times 12.47} = 277.79 \ \text{(A)} \]

在功率因数为0.9，滞后电压的情况下，负荷电流矩阵为

\[ [I_{abc}]_m = \begin{bmatrix} 277.79\angle-25.84\\ 277.79\angle-145.84\\ 277.79\angle94.16 \end{bmatrix} \ \text{(A)} \]

计算节点$n$处的线对地电压为

\[ [VLG_{abc}]_n = [a]\cdot [VLG_{abc}]_m+[b]\cdot [I_{abc}]_m=\begin{bmatrix} 8213.1\angle3.6876\\ 7977.7\angle-115.95\\ 8075.4\angle124.63 \end{bmatrix} \ \text{(V)} \]

注意，即使负荷（节点$m$）处的电压和电流完全对称，节点$n$处的电压也不对称，这是相间相互耦合所导致的。在电力系统中，电压不对称的程度值得关注，因为某些电气设备对于不对称电压非常敏感，例如三相感应电动机的操作特性。

\[\begin{align} \begin{split} \left | V_{\text{average}} \right | &= \frac{\left | V_{ag} \right |_n + \left | V_{bg} \right |_n+\left | V_{cg} \right |_n}{3} = \frac{8213.1+7977.7+8075.4}{3}=8088.7 \notag \\ \left( V_{\text{deviation}} \right)_{\text{max}} &= 8213.1-8088.7 = 124.4 \ \text{V} \notag \\ V_{\text{unbalance}} &= \frac{124.4}{8088.7}\times 100\% = 1.538\% \notag \end{split} \end{align}\]

选择额定线路接地电压（7199.56 V）为基准值，母线$n$处的单位电压为

\[ \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_n = \frac{1}{7199.56}\begin{bmatrix} 8213.1\angle3.6876\\ 7977.7\angle-115.95\\ 8075.4\angle124.63 \end{bmatrix} =\begin{bmatrix} 1.1408\angle3.6876\\ 1.1081\angle-115.95\\ 1.1217\angle124.63 \end{bmatrix} \]

通过将电压转换为标幺值，很容易看出，$A$相的电压降为14.08%，$B$相为10.81%，$C$相为12.17%。

节点$n$处的线电流计算结果是：

\[ [I_{abc}]_n = [c]\cdot [VLG_{abc}]_m + [d]\cdot [I_{abc}]_m = [I_{abc}]_m = \begin{bmatrix} 277.79\angle-25.84\\ 277.79\angle-145.84\\ 277.79\angle94.16 \end{bmatrix} \ \text{(A)} \]

实际上，节点$n$处的线电流与节点$m$处的对称负荷电流存在非常小的差异，这是节点$n$处的不对称电压和线路段的并联导纳产生的。在本例中，由于忽略了并联导纳，因此可以认为节点$n$处的线电流与节点$m$处的对称负荷电流近似相等。

改进的线路模型

一条线路的并联导纳很小时就可以忽略不计，下图所示是忽略并联导纳的改进线路段模型。当忽略并联导纳时，广义矩阵变为

\[\begin{align} [a] & = [U] \label{6.30} \\ [b] & = [Z_{abc}] \label{6.31} \\ [c] & = [0] \label{6.32} \\ [d] & = [U] \label{6.33} \\ [A] & = [U] \label{6.34} \\ [B] & = [Z_{abc}] \label{6.35} \end{align}\]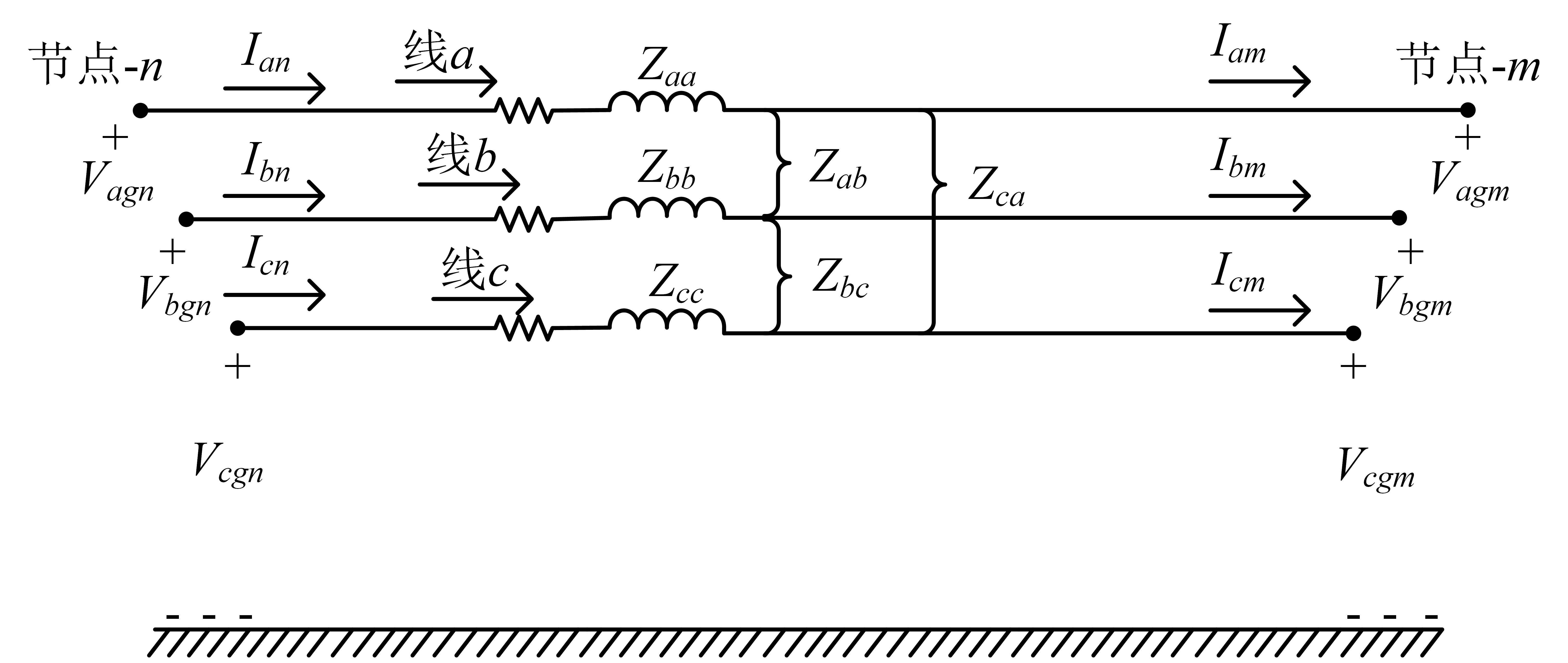 $忽略并联导纳的改进线路段模型\label{p6.2}$

如果线路是三线三角形，则线路上的电压降必须根据线间电压和线电流而定。但是，可以使用等效线电压，以便使上述的方程式仍然适用。

根据图中线路的线电压写出电压降方程式，结果如下：

\[\begin{equation} \begin{bmatrix} V_{ab}\\ V_{bc}\\ V_{ca} \end{bmatrix}_n = \begin{bmatrix} V_{ab}\\ V_{bc}\\ V_{ca} \end{bmatrix}_m + \begin{bmatrix} V_{\text{drop}a}\\ V_{\text{drop}b}\\ V_{\text{drop}c} \end{bmatrix} - \begin{bmatrix} V_{\text{drop}b}\\ V_{\text{drop}c}\\ V_{\text{drop}a} \end{bmatrix} \label{6.36} \end{equation}\]

其中:

\[\begin{equation} \begin{bmatrix} V_{\text{drop}a}\\ V_{\text{drop}b}\\ V_{\text{drop}c} \end{bmatrix}=\begin{bmatrix} Z_{aa} & Z_{ab} & Z_{ac}\\ Z_{ba} & Z_{bb} & Z_{bc}\\ Z_{ca} & Z_{cb} & Z_{cc} \end{bmatrix}\cdot \begin{bmatrix} I_{\text{line}a}\\ I_{\text{line}b}\\ I_{\text{line}c} \end{bmatrix} \label{6.37} \end{equation}\]

展开$a$-$b$相：

\[\begin{equation} V_{abn} = V_{abm}+V_{\text{drop}a} - V_{\text{drop}b} \label{6.38} \end{equation}\]

又有

\[\begin{equation} \label{6.39} \begin{split} V_{abn} &= V_{ann}-V_{bnn}\\ V_{abm} &= V_{anm}-V_{bnm} \end{split} \end{equation}\]

代入得：

\[\begin{equation} V_{ann}-V_{bnn} = V_{anm}-V_{bnm}+V_{\text{drop}a}-V_{\text{drop}b} \label{6.40} \end{equation}\]

根据等效线路中性线电压，该公式可以分解为两部分：

\[\begin{equation} \label{6.41} \begin{split} V_{ann} &= V_{anm}+V_{\text{drop}a}\\ V_{bnn} &= V_{bnm}+V_{\text{drop}b} \end{split} \end{equation}\]

这里的结论是，可以在三线三角形线中使用等效的相线到中性线电压。这是非常重要的，因为这样就使得对四线星形和三线三角形系统的分析方式相同。

例题八

例2.7的线路在节点$m$处接入不对称负荷，假设电源端电压（节点$n$）是三相对称的，线电压为12.47 kV。对称的线对地电压为

\[ [VLG_{abc}]_n = \begin{bmatrix} 7199.56\angle0\\ 7199.56\angle-120\\ 7199.56\angle120 \end{bmatrix} \ \text{(V)} \]

在电源端量测的不对称电流由下式给出：

\[ \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_n = \begin{bmatrix} 249.97\angle{-24.5}\\ 277.56\angle{-145.8}\\ 305.54\angle{95.2} \end{bmatrix} \ \text{(A)} \]

使用改进的线路模型计算负荷端（节点$m$）的线对地和线对线电压。并计算不对称电压和负荷的复数功率。

解答

改进后的线路模型的$[A]$和$[B]$矩阵是：

\[\begin{equation} \nonumber \begin{split} [A] &= [U] = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\\ [B] &= [Z_{abc}] = \begin{bmatrix} 2.923+\text{j}5.890 & 1.051+\text{j}2.902 & 1.035+\text{j}2.301\\ 1.051+\text{j}2.902 & 2.980+\text{j}5.727 & 1.064+\text{j}2.496\\ 1.035+\text{j}2.301 & 1.064+\text{j}2.496 & 2.948+\text{j}5.819 \end{bmatrix} \ \text{(}\Omega \text{)} \end{split} \end{equation}\]

在近似模型中：

\[ \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_m = \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_n = \begin{bmatrix} 249.97\angle{-24.5}\\ 277.56\angle{-145.8}\\ 305.54\angle{95.2} \end{bmatrix} \ \text{(A)} \]

负荷端的线对地电压为

\[ [VLG_{abc}]_m = [A]\cdot [VLG_{abc}]_n - [B]\cdot [I_{abc}]_m = \begin{bmatrix} 6457.8\angle{-4.0666}\\ 6352.2\angle{-124.0828}\\ 6284.8\angle{112.1210} \end{bmatrix} \ \text{(V)} \]

在这种情况下，平均负荷电压为

\[ \left | V_{\text{average}} \right | = \frac{6457.8+6352.2+6284.8}{3} = 6364.9 \ \text{(V)} \]

$a$相电压与平均电压的偏差最大，因此：

\[\begin{gather*} \left( V_{\text{deviation}} \right)_{\text{max}} = \left | 6457.8-6364.9 \right | = 92.9 \ \text{(V)} \\ V_{\text{unbalance}} = \frac{92.9}{6364.9}\times 100\% = 1.460\% \end{gather*}\]

负荷端的线电压可以由下式计算：

\[ \begin{bmatrix} V_{ab}\\ V_{bc}\\ V_{ca} \end{bmatrix} = \begin{bmatrix} 1 & -1 & 0\\ 0 & 1 & -1\\ -1 & 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} 6457.8\angle{-4.0666}\\ 6352.2\angle{-124.0828}\\ 6284.8\angle{112.1210} \end{bmatrix}=\begin{bmatrix} 11094.9\angle{25.653}\\ 11147.3\angle{-96.144}\\ 10817.8\angle{144.512} \end{bmatrix} \ \text{(V)} \]

负荷的视在功率为

\[ \begin{bmatrix} S_a\\ S_b\\ S_c \end{bmatrix} = \frac{1}{1000} \begin{bmatrix} V_{ag}\cdot I_{a}^{\ast }\\ V_{bg}\cdot I_{b}^{\ast }\\ V_{cg}\cdot I_{c}^{\ast } \end{bmatrix} = \begin{bmatrix} 1614.26\angle{20.43}\\ 1763.12\angle{21.72}\\ 1920.26\angle{16.92} \end{bmatrix} \ \text{(kVA)} \]

近似线路段模型

很多时候，线路的唯一已知数据是正序和零序阻抗。近似线路段模型可以通过应用来自对称分量理论的反向阻抗变换来建立。

使用已知的正序和零序阻抗，序阻抗矩阵由下式给出：

\[\begin{equation} [Z_{\text{seq}}] = \begin{bmatrix} Z_0 & 0 & 0\\ 0 & Z_+ & 0\\ 0 & 0 & Z_+ \end{bmatrix} \label{6.42} \end{equation}\]

通过反向阻抗变换产生以下近似相阻抗矩阵：

\[\begin{equation} [Z_{\text{approx}}] = [A_\text{s}]\cdot [Z_{\text{seq}}]\cdot [A_\text{s}]^{-1} \label{6.43} \end{equation}\]

即

\[\begin{equation} [Z_{\text{approx}}] = \frac{1}{3} \begin{bmatrix} (2 Z_+ +Z_0) & (Z_0-Z_+) & (Z_0-Z_+)\\ (Z_0-Z_+) & (2 Z_+ +Z_0) & (Z_0-Z_+)\\ (Z_0-Z_+) & (Z_0-Z_+) & (2 Z_+ +Z_0) \end{bmatrix} \label{6.44} \end{equation}\]

请注意，近似相阻抗矩阵的特点是三个对角项相等，所有非对角项相等。如果假设该线路存在换位，则结果也是相同的。应用近似阻抗矩阵计算节点$n$处的电压为

\[\begin{equation} \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_n = \begin{bmatrix} V_{ag}\\ V_{bg}\\ V_{cg} \end{bmatrix}_m + \frac{1}{3} \begin{bmatrix} (2 Z_+ +Z_0) & (Z_0-Z_+) & (Z_0-Z_+)\\ (Z_0-Z_+) & (2 Z_+ +Z_0) & (Z_0-Z_+)\\ (Z_0-Z_+) & (Z_0-Z_+) & (2 Z_+ +Z_0) \end{bmatrix}\cdot \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_m \label{6.45} \end{equation}\]

在矩阵形式中，上式变为

\[\begin{equation} [VLG_{abc}]_n = [VLG_{abc}]_m + [Z_{\text{approx}}]\cdot [I_{abc}]_m \label{6.46} \end{equation}\]

形式为

\[\begin{equation} [VLG_{abc}]_n = [a]\cdot [VLG_{abc}]_m + [b]\cdot [I_{abc}]_m \label{6.47} \end{equation}\]

式中：$[a]$为单位矩阵；$[b]$ = [$Z_{\text{approx}}$]。

展开得到近似线路段模型的等效电路。求解式中节点$n$的$a$相电压：

\[\begin{align} \label{6.49} \begin{split} V_{agn} &= V_{agm}+ \frac{1}{3} \left[(2Z_+ +Z_0)I_a + (Z_0 - Z_+)I_b + (Z_0 - Z_+)I_c \right] \\ ~ & = V_{agm} + \frac{1}{3} \left \{ (2Z_+ + Z_0)I_a + (Z_0-Z_+)I_b+(Z_0-Z_+)I_c + (Z_0-Z_+)I_a -(Z_0-Z_+)I_a\right \} \\ ~ & = V_{agm} + \frac{1}{3} \left[(3Z_+)I_a +(Z_0 - Z_+)(I_a + I_b +I_c) \right] \\ ~ & = V_{agm} + Z_+ I_a +\frac{Z_0 - Z_+}{3}(I_a+ I_b + I_c) \end{split} \end{align}\]

对$b$和$c$相同样计算：

\[\begin{equation} V_{bgn} = V_{bgm} + Z_+ I_b +\frac{Z_0 - Z_+}{3}(I_a+ I_b + I_c) \label{6.50} \end{equation}\] \[\begin{equation} V_{cgn} = V_{cgm} + Z_+ I_c +\frac{Z_0 - Z_+}{3}(I_a+ I_b + I_c) \label{6.51} \end{equation}\]

下图显示了近似线路段模型。由于没有对相线的相互耦合进行建模，因此该图是线路段的简单等效电路，必须注意等效电路只能在假定线路换位时使用。

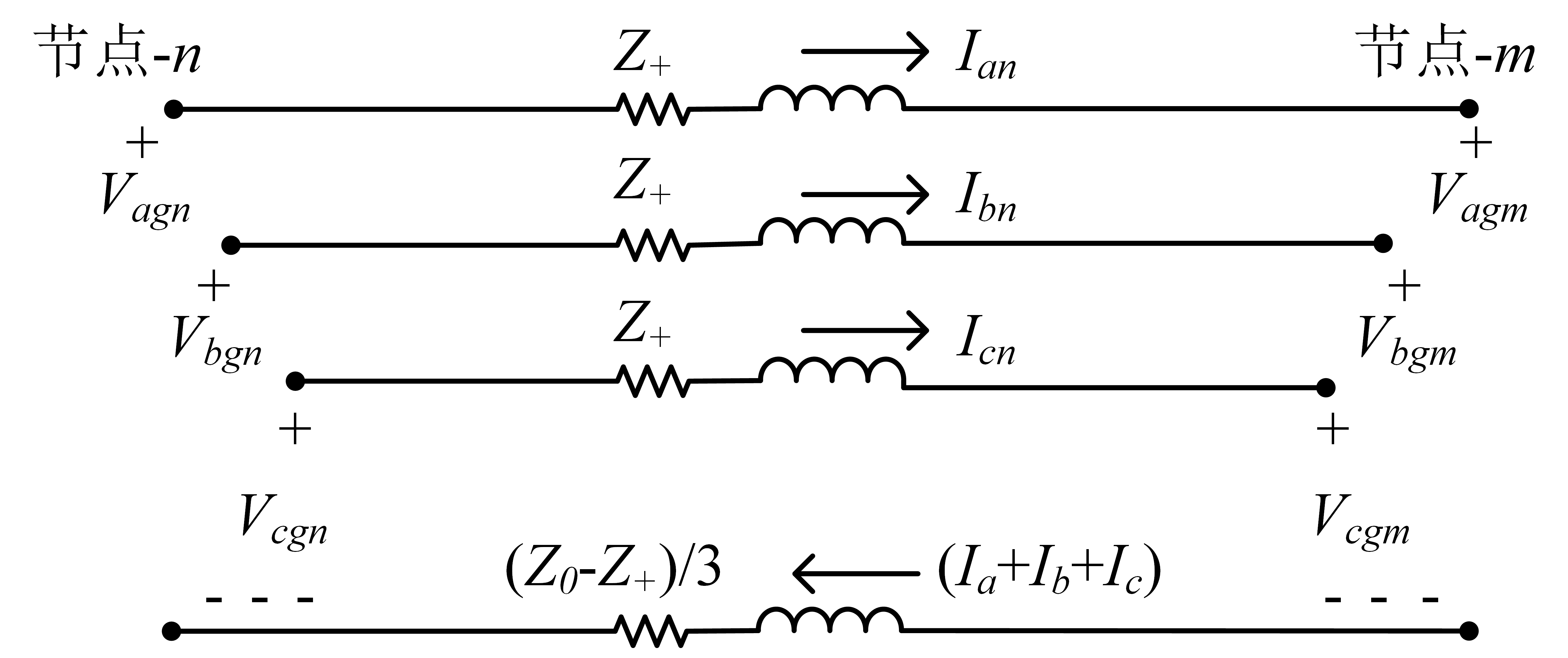
$近似线路段模型\label{p6.3}$

例题九

假设线路已换位，分析例2.1的线路段。在例2.1中，正序阻抗和零序阻抗为

\[\begin{gather*} z_+ = 0.1900 + \text{j}0.3246\ \text{(}\Omega \text{/km)}\\ z_0 = 0.5050 + \text{j}1.0945\ \text{(}\Omega \text{/km)} \end{gather*}\]

假设节点$m$的负荷与例2.7相同，在该负荷条件下计算电源端（节点$n$）处的电压和电流。

解答

序阻抗矩阵为

\[ [Z_{\text{seq}}] = \begin{bmatrix} 0.5050 + \text{j}1.0945 & 0 & 0\\ 0 & 0.1900 + \text{j}0.3246 & 0\\ 0 & 0 & 0.1900 + \text{j}0.3246 \end{bmatrix} \ \text{(}\Omega \text{/km)} \]

进行反向阻抗变换得到近似相阻抗矩阵：

\[\begin{align} [Z_{\text{approx}}] & = [A_\text{s}]\cdot [Z_{\text{seq}}]\cdot [A_\text{s}]^{-1} \notag \\ ~ & = \begin{bmatrix} 0.2950+ \text{j}0.5812 & 0.1050+ \text{j}0.2566 & 0.1050+ \text{j}0.2566\\ 0.1050+ \text{j}0.2566 & 0.2950+ \text{j}0.5812 & 0.1050+ \text{j}0.2566\\ 0.1050+ \text{j}0.2566 & 0.1050+ \text{j}0.2566 & 0.2950+ \text{j}0.5812 \end{bmatrix} \ \text{(}\Omega \text{/km)} \notag \end{align}\]

对于长度为10000 m的线路，相阻抗矩阵和$[b]$矩阵是：

\[\begin{align} [b] & = [Z_{\text{approx}}] =10 [z_{\text{approx}}] \notag \\ ~ & = \begin{bmatrix} 2.950+ \text{j}5.812 & 1.050+ \text{j}2.566 & 1.050+ \text{j}2.566\\ 1.050+ \text{j}2.566 & 2.950+ \text{j}5.812 & 1.050+ \text{j}2.566\\ 1.050+ \text{j}2.566 & 1.050+ \text{j}2.566 & 2.950+ \text{j}5.812 \end{bmatrix} \ \text{(}\Omega \text{)} \notag \end{align}\]

从例2.7可知，节点$m$的电压和电流是：

\[\begin{align} [VLG_{abc}]_m & = \begin{bmatrix} 7199.56\angle{0}\\ 7199.56\angle{-120}\\ 7199.56\angle{120} \end{bmatrix} \ \text{(V)} \notag \\ [I_{abc}]_m & = \begin{bmatrix} 277.79\angle{-25.84}\\ 277.79\angle{-145.84}\\ 277.79\angle{94.16} \end{bmatrix} \ \text{(A)} \notag \end{align}\]

根据公式可得:

\[ [VLG_{abc}]_n = [a]\cdot [VLG_{abc}]_m + [b]\cdot [I_{abc}]_m = \begin{bmatrix} 8088.5\angle{4.123}\\ 8088.5\angle{-115.877}\\ 8088.5\angle{124.123} \end{bmatrix} \ \text{(V)} \]

可以发现，计算得到的电压是对称的。节点$n$处的$V_{ag}$ 也可以使用$V_{agn}$公式来计算（式中$Z_+$和$Z_0$与题干中给出的不同，这里是乘了长度10 km后的总阻抗）：

\[ V_{agn} = V_{agm} + Z_+\cdot I_a +\frac{(Z_0 - Z_+)}{3}\cdot (I_a+ I_b + I_c) \]

由于电流是对称的，这个等式简化为 \[\begin{align} V_{agn} & = V_{agm} + Z_+\cdot I_a \notag \\ & = 7199.56\angle{0} + (1.900 + \text{j}3.246)\times 277.79\angle{-25.84} = 8088.5\angle{4.123} \ \text{(V)} \notag \end{align}\]

可以注意到，当负荷对称且假设线路换位，三相线可以用简单的单相模型进行分析。

例题十

使用例2.8中节点$n$处的对称电压和不对称电流以及近似线路段模型来计算节点$m$处的电压和电流。

解答

从例2.8可知，节点$n$处的电压和电流为

\[\begin{align} [VLG_{abc}]_n & = \begin{bmatrix} 7199.56\angle0\\ 7199.56\angle-120\\ 7199.56\angle120 \end{bmatrix} \ \text{(V)} \notag \\ \begin{bmatrix} I_a\\ I_b\\ I_c \end{bmatrix}_n & = \begin{bmatrix} 249.97\angle{-24.5}\\ 277.56\angle{-145.8}\\ 305.54\angle{95.2} \end{bmatrix} \ \text{(A)} \notag \end{align}\]

近似线路段模型的$[A]$和$[B]$矩阵是

= 单位矩阵，= [$Z_{\text{approx}}$]

节点$m$处的电压由下式计算：

\[ [VLG_{abc}]_m = [A]\cdot [VLG_{abc}]_n - [B]\cdot [I_{abc}]_n =\begin{bmatrix} 6596.5\angle{-4.450}\\ 6251.8\angle{-124.313}\\ 6260.4\angle{112.678} \end{bmatrix} \ \text{(V)} \]

不对称电压为

\[\begin{align} V_{\text{average}} & = \frac{6596.5+6251.8+6260.4}{3} = 6369.6 \ \text{(V)} \notag \\ \left( V_{\text{deviation}} \right)_{\text{max}} & = \left | 6596.5-6369.6 \right | = 226.9 \ \text{(V)} \notag \\ V_{\text{unbalance}} & = \frac{226.9}{6369.6}\times 100\% = 3.5622\% \notag \end{align}\]

可以发现，近似模型得到了比精确模型更高的不对称电压。

总结

串联阻抗计算：利用修正的Carson方程可以简化相阻抗的计算。当使用修正的Carson公式时，不需要做任何假设，例如线路的换位。由于电压降是配电线路上的主要问题，因此用于线路的阻抗必须尽可能精确。

并联导纳计算：配电线路通常很短，并联导纳可以忽略不计。对一些长的、轻载的架空线路，则应该计算并联导纳。地下电缆单位千米的并联导纳比架空线路高得多，某些情况下，地下电缆的并联导纳也应包括在分析过程中。

配电网络线路模型

精确线路段模型：不使用近似值，即使用相阻抗矩阵（假定不换位）以及并联导纳矩阵。
改进的线路模型：忽略了并联导纳。
近似线路段模型：忽略并联导纳，并假设线路的正序和零序阻抗是已知参数，据此求得近似相阻抗矩阵。

对于三线模型本章建立了广义矩阵方程，这些方程使用广义矩阵$[a]$、$[b]$、$[c]$、$[d]$、$[A]$和$[B]$。例题表明，由于并联导纳非常小，广义矩阵通常可以忽略并联导纳。但是有些情况下并联导纳不应该被忽略，如长距离、轻负载的线路以及许多地下线路。