智能配电网络建模与分析
主动配电网与微电网技术
2020年
本次课内容
(1)理解主动配电网和微电网的概念
(2)掌握分布式电源的建模方法
(3)了解主动配电网和微电网的分析方法
基本概念
主动配电网(Active Distribution Network)是采用主动管理分布式电源、储能设备和客户双向负荷的模式,具有灵活拓扑结构的公用配电网。
主动配电网的目标是在保证电网运行可靠性的前提下,增加现有配电网对可再生能源发电的容纳能力。
微电网是指由分布式电源、储能装置、能量转换装置、负荷、监控和保护装置等组成的小型发配电系统,是实现主动配电网的一种有效方式。其日常运行有“并网运行”和“孤岛运行”两种运行模式。
建模
在对配电网进行分析之前必须先针对不同的研究目的建立准确有效的数学模型。针对分布式电源,通常从宏观和微观两个角度进行分析和建模,包括系统级建模和元件级建模两个方面。
系统级建模
系统级建模是将多个分布式电源看作配电网中一个整体进行简化,在研究时只关注配电网与分布式电源整体外部特性的相互作用及影响。
应用:对同类型的分布式电源进行综合建模,主要包含风电场动态等值建模和基于广义负荷建模理论的多分布式电源综合建模。
分布式电源接入电网的运行方式主要分为两类:以微电网的形式孤岛运行;与主网并网运行。按照并网特性,可将常见的分布式电源分为四类:同步发电机、异步发电机、电力电子接口并网型电源和双馈发电机,这里我们主要介绍前三类分布式电源的模型。
并网型同步发电机
采用同步发电机并网的主要是分布式热电联产机组、小型水电机组等。其建模可分为:三相平衡时的同步发电机模型和三相不平衡时的同步发电机模型。对于前者的研究已较为成熟,可以参考《电机学》等教材,本节主要分析三相不平衡时的建模。
控制方式:三相总加功率为恒定量
首先应用对称分量法建立同步发电机序分量模型。
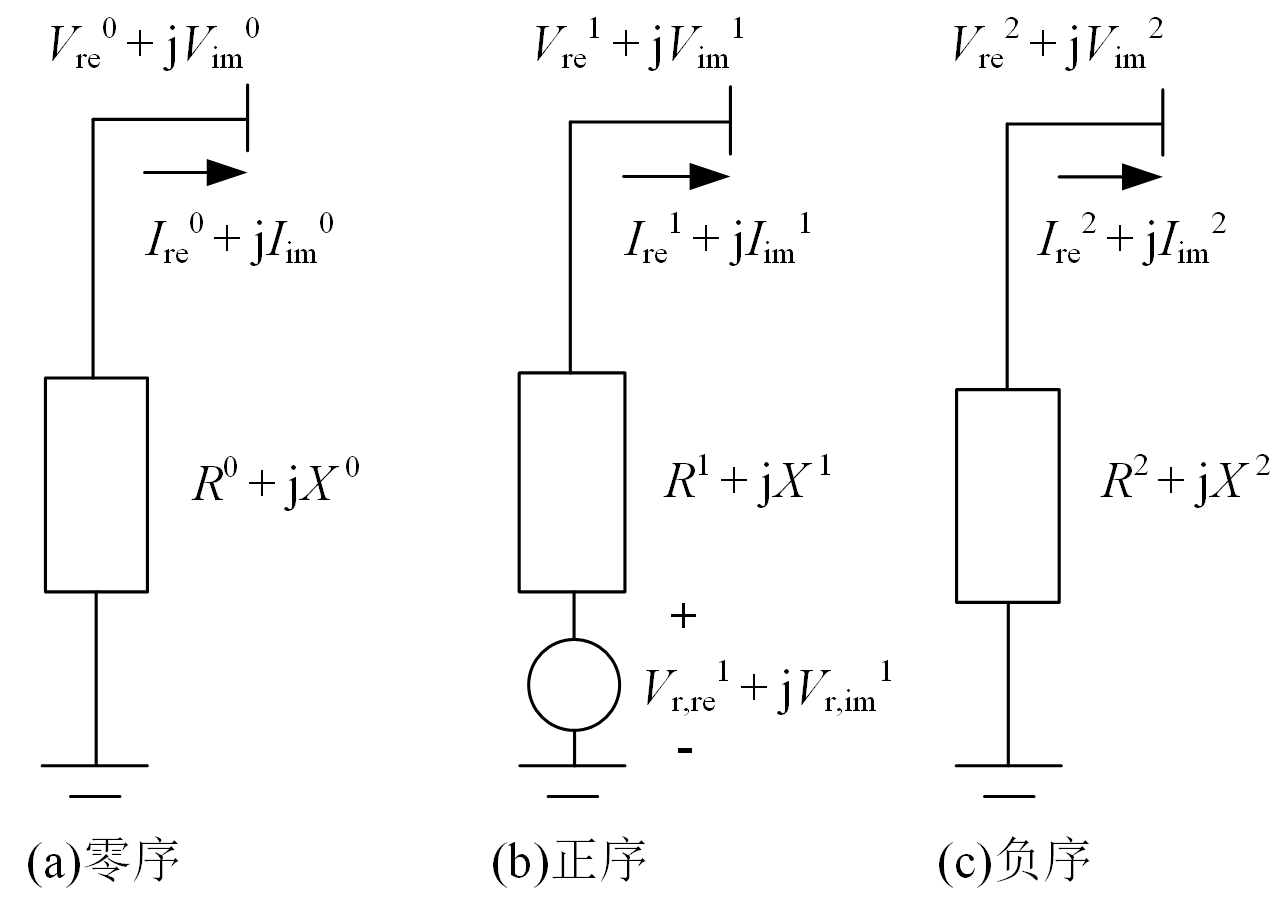
同步发电机的控制系统分为三部分,包括有功功率的控制、不平衡分量的控制和无功功率或电压的控制。
同步发电机有功功率控制
同步发电机的有功功率控制方程包含两类:总的有功功率控制为常数,正序有功功率控制为常数。一般我们采用第一类,对应的控制方程为
\[\begin{eqnarray} \label{eps11.1} {\rm{Re}}\left [ 3\sum_{p=0,1,2}^{} \left ( V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p} \right ) \left ( I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p} \right )\right ]+3\sum_{p=0,1,2}^{}\left [ \left ( I_{\rm{re}}^{p} \right )^{2}+\left ( I_{\rm{im}}^{p} \right )^{2} \right ]R^{p}=P_{\rm{sp}} \end{eqnarray}\]式中:\(P_{\rm{sp}}\)是机械功率。
同步发电机不平衡分量控制
当采用序分量来描述一般同步发电机的励磁电压时,励磁电压序分量中,励磁电压零序、负序分量为零,正序分量满足线性电气约束,与此对应的发电机不平衡约束方程为
\[\begin{eqnarray} \label{eps11.2} \left\{\begin{aligned} & V_{\rm{r,re}}^{0}={\rm{Re}}\left [ \left ( I_{\rm{re}}^{0}+{\rm{j}}I_{\rm{im}}^{0} \right )\left ( R^{0}+{\rm{j}}X^{0} \right )+\left ( V_{\rm{re}}^{0}+{\rm{j}}V_{\rm{im}}^{0} \right ) \right ]=0\\ & V_{\rm{r,im}}^{0}={\rm{Im}}\left [ \left ( I_{\rm{re}}^{0}+{\rm{j}}I_{\rm{im}}^{0} \right )\left ( R^{0}+{\rm{j}}X^{0} \right )+\left ( V_{\rm{re}}^{0}+{\rm{j}}V_{\rm{im}}^{0} \right ) \right ]=0\\ & V_{\rm{r,re}}^{2}={\rm{Re}}\left [ \left ( I_{\rm{re}}^{2}+{\rm{j}}I_{\rm{im}}^{2} \right )\left ( R^{2}+{\rm{j}}X^{2} \right )+\left ( V_{\rm{re}}^{2}+{\rm{j}}V_{\rm{im}}^{2} \right ) \right ]=0\\ & V_{\rm{r,im}}^{2}={\rm{Im}}\left [ \left ( I_{\rm{re}}^{2}+{\rm{j}}I_{\rm{im}}^{2} \right )\left ( R^{2}+{\rm{j}}X^{2} \right )+\left ( V_{\rm{re}}^{2}+{\rm{j}}V_{\rm{im}}^{2} \right ) \right ]=0\\ & V_{\rm{r,re}}^{1}={\rm{Re}}\left [ \left ( I_{\rm{re}}^{1}+{\rm{j}}I_{\rm{im}}^{1} \right )\left ( R^{1}+{\rm{j}}X^{1} \right )+\left ( V_{\rm{re}}^{1}+{\rm{j}}V_{\rm{im}}^{1} \right ) \right ]\\ & V_{\rm{r,im}}^{1}={\rm{Im}}\left [ \left ( I_{\rm{re}}^{1}+{\rm{j}}I_{\rm{im}}^{1} \right )\left ( R^{1}+{\rm{j}}X^{1} \right )+\left ( V_{\rm{re}}^{1}+{\rm{j}}V_{\rm{im}}^{1} \right ) \right ] \end{aligned}\right. \end{eqnarray}\]电压或无功功率的控制
在微电网运行时,同步发电机常常采用定电圧控制,方式有很多种,既可以控制三相电压的幅值均值为常数,也可以控制某一相电压的幅值均值为常数,还能控制正序电压的幅值为常数。
正序电压的约束方程为
\[\begin{eqnarray} \label{eps11.3} \sqrt{\left ( V_{\rm{re}}^{1} \right )^{2}+\left ( V_{\rm{im}}^{1} \right )^{2}}=V_{\rm{sp}}^{1} \end{eqnarray}\]分布式电源并网运行时常采用定无功控制,控制方程为
\[\begin{eqnarray} \label{eps11.4} {\rm{Im}}\left [ 3\sum_{p=0,1,2}^{}\left ( V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p} \right )\left ( I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p} \right ) \right ]=Q_{\rm{sp}} \end{eqnarray}\]由于励磁电压的幅值存在限幅环节,所以电压约束或无功约束方程可以转换为限幅约束方程
\[\begin{eqnarray} \label{eps11.5} \sqrt{\left ( V_{\rm{re}}^{1} \right )^{2}+\left ( V_{\rm{im}}^{1} \right )^{2}}=V_{\rm{lim}} \end{eqnarray}\]至此我们得到所有控制方程,潮流计算中的待求量只有8个,为\(I_{\rm{re}}^{0}\)、\(I_{\rm{im}}^{0}\)、\(I_{\rm{re}}^{1}\)、\(I_{\rm{im}}^{1}\)、\(I_{\rm{re}}^{2}\)、\(I_{\rm{im}}^{2}\)、\(V_{\rm{re}}^{1}\)、\(V_{\rm{im}}^{1}\),所以建立的模型可解。
并网型异步发电机
异步发电机主要应用于微型燃气轮机、定速风机及半定速(动态转子电阻)风机等一系列分布式发电设备。
本节主要介绍动态转子电阻异步风机的三相稳态模型。
动态转子电阻异步风机:也称为最优滑差风机,通过功率控制器和转速控制器控制注入电网的三相有功功率和风机转速(滑差)。
并网型异步发电机(续)
由于异步发电机通常外接三角形变压器并网,因此可以认为异步发电机和电网间只存在正序和负序通路。异步发电机序分量模型如下图所示。
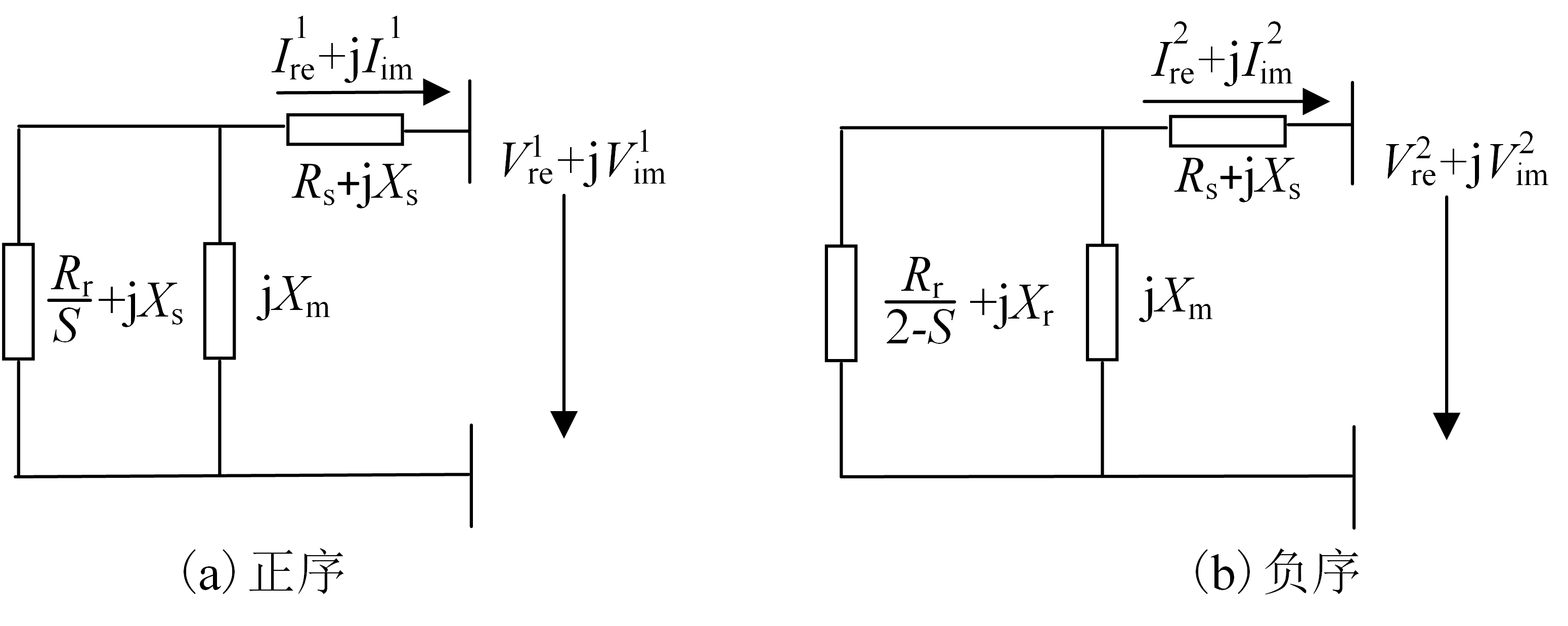
异步发电机控制方程
有功功率控制方程为
\[\begin{eqnarray} \label{eps11.6} {\rm{Re}}\left[3\sum_{p=0,1,2}(V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p})(I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p}) \right] = P_{\rm{sp}} \end{eqnarray}\]式中:\(P_{\rm{sp}}\)是三相总加有功功率。
正序和负序分别满足以下方程
\[\begin{gather} -\frac{V_{\rm{re}}^{1}+{\rm{j}}V_{\rm{im}}^{1}}{I_{\rm{re}}^{1}+{\rm{j}}I_{\rm{im}}^{1}} = R_{\rm{s}} +{\rm{j}}X_{\rm{s}} + \frac{{\rm{j}}X_{\rm{m}}(R_{\rm{r}}+{\rm{j}}{s}X_{\rm{r}})}{{\rm{j}}{s}X_{\rm{m}}+R_{\rm{r}}+{\rm{j}}{s}X_{\rm{r}}} \label{eps11.7}\\ -\frac{V_{\rm{re}}^{2}+{\rm{j}}V_{\rm{im}}^{2}}{I_{\rm{re}}^{2}+{\rm{j}}I_{\rm{im}}^{2}} = R_{\rm{s}} +{\rm{j}}X_{\rm{s}} + \frac{{\rm{j}}X_{\rm{m}}(R_{\rm{r}}+{\rm{j}}(2-{s})X_{\rm{r}})}{{\rm{j}}{s}X_{\rm{m}}+R_{\rm{r}}+{\rm{j}}(2-{s})X_{\rm{r}}} \label{eps11.8} \end{gather}\]零序约束方程
\[\begin{eqnarray} \label{eps11.9} I_{\rm{re}}^{0}+{\rm{j}}I_{\rm{im}}^{0}=0 \end{eqnarray}\]在潮流计算中,待求变量有7个:\(I_{\rm{re}}^{0}\)、\(I_{\rm{im}}^{0}\)、\(I_{\rm{re}}^{1}\)、\(I_{\rm{im}}^{1}\)、\(I_{\rm{re}}^{2}\)、\(I_{\rm{im}}^{2}\)和\(R_{\rm{r}}\),之前刚好给出了7个方程,因此模型可解。
换流器并网型分布式电源
换流器并网型分布式电源:采用电力电子接口方式并网的分布式电源,如蓄电池、光伏发电设备和配网静止同步补偿器等。其中采用的换流器主要是电压型换流器(VSC)。
任何形式的分布式电源在采用VSC并网时都需要先转为直流电再经过DC-AC逆变并网。图片中DC-Link表示直流环节,经逆变、滤波后并网,滤波阻抗\(R_{f}+{\rm{j}}X_{f}\),\(n\)为三相四线制换流器中线,由于VSC并网型分布式电源通常外接三角形连接变压器,因此这里不考虑零序通路。
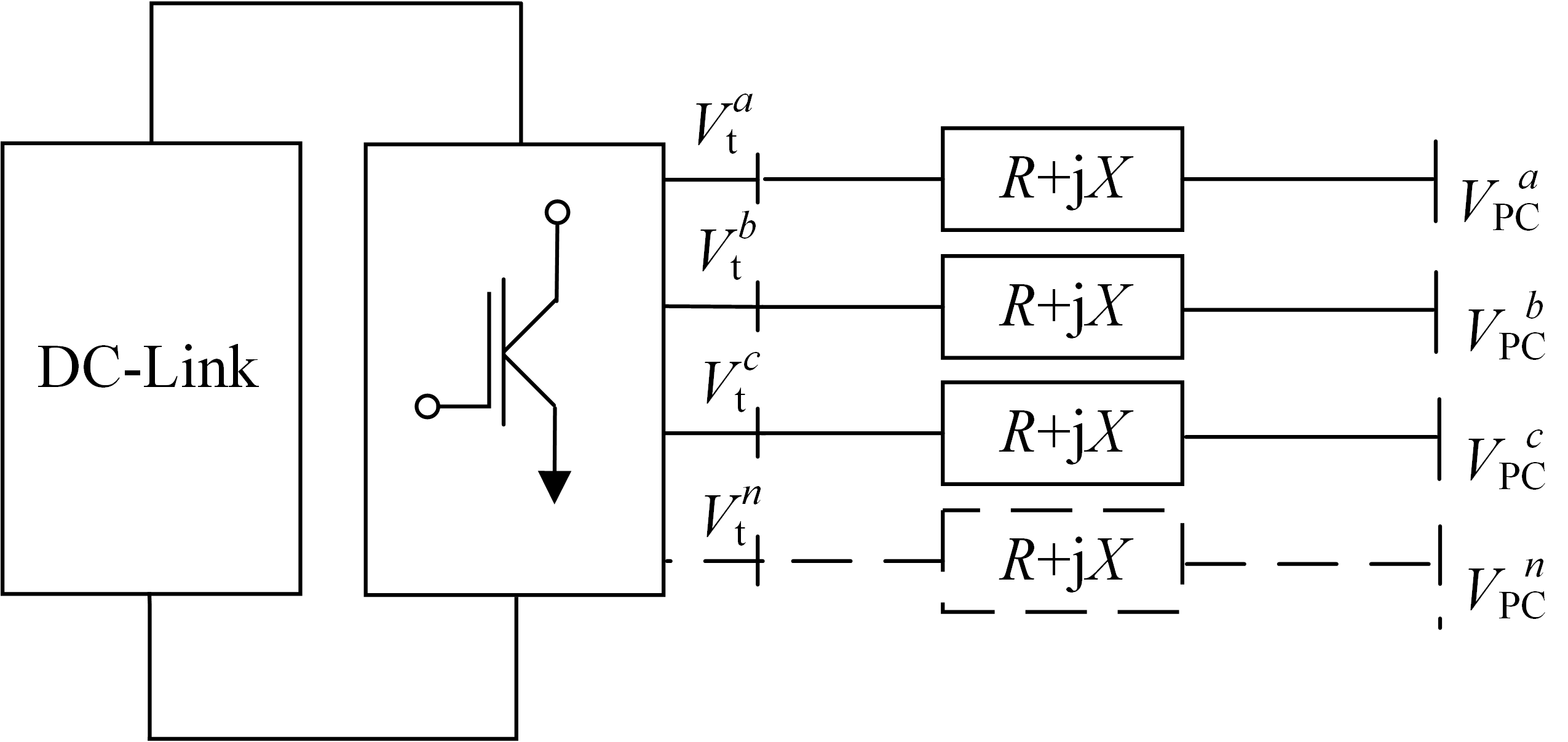
控制方程
VSC并网分布式电源可以划分为PV节点、PQ节点和孤网状态下的PQ(V)节点。
三种类型的节点有功功率控制方程均为
\[\begin{eqnarray} \label{eps11.10} {\rm{Re}}\left [3\sum_{p=0,1,2}(V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p})(I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p}) \right ]=P_{\rm{sp}} \end{eqnarray}\]当分布式电源容量达到具有电压支撑能力时,可作为PV节点。此类发电机节点正序电压控制方程为
\[\begin{eqnarray} \label{eps11.11} \sqrt{(V_{\rm{re}}^{1})^{2}+(V_{\rm{im}}^{1})^{2}}=V_{\rm{sp}}^{1} \end{eqnarray}\]VSC并网型分布式电源对不平衡分量控制方式可分为三种:
①换流器出口负序电压\(V_{\rm{re}}^{2}+{\rm{j}}V_{\rm{im}}^{2}=0\),对应的控制方程是
\[\begin{gather} I_{\rm{re}}^{2}=-\frac{V_{\rm{re}}^{2}R^{2}+V_{\rm{im}}^{2}X^{2}}{(R^{2})^{2}+(X^{2})^{2}} \label{eps11.12}\\ I_{\rm{im}}^{2}=-\frac{-V_{\rm{re}}^{2}X^{2}+V_{\rm{im}}^{2}R^{2}}{(R^{2})^{2}+(X^{2})^{2}} \label{eps11.13} \end{gather}\]②VSC并网型分布式电源注入电网的负序电流控制为0,对应的控制方程是
\[\begin{gather} I_{\rm{re}}^{2}=0 \label{eps11.14}\\ I_{\rm{im}}^{2}=0 \label{eps11.15} \end{gather}\]③在不平衡系统下运行,为抑制直流部分电容器产生的纹波,应对发电机注入电网的瞬时功率的二倍工频波动量进行控制,控制方程为
\[\begin{gather} V_{\rm{re}}^{1}I_{\rm{re}}^{2}+V_{\rm{im}}^{1}I_{\rm{im}}^{2}+V_{\rm{re}}^{2}I_{\rm{re}}^{1}+V_{\rm{im}}^{2}I_{\rm{im}}^{1}=0 \label{eps11.16}\\ V_{\rm{im}}^{2}I_{\rm{re}}^{1}-V_{\rm{re}}^{1}I_{\rm{im}}^{1}-V_{\rm{im}}^{1}I_{\rm{re}}^{1}+V_{\rm{re}}^{2}I_{\rm{im}}^{1}=0 \label{eps11.17} \end{gather}\]对于PQ节点来说,其无功控制方程为
\[\begin{eqnarray} \label{eps11.18} {\rm{Im}}\left [3\sum_{p=0,1,2}(V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p})(I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p}) \right ]=Q_{\rm{sp}} \end{eqnarray}\]PQ节点对于不平衡分量控制方程与PV节点相同。
对于PQ(V)节点而言,分布式发电运行在孤岛状态时,为了使VSC并网型分布式电源具有一定电压支撑能力,需增加无功电压下垂控制环节。控制方程为
\[\begin{eqnarray} \label{eps11.19} {\rm{Im}}\left [ 3\sum_{p=0,1,2}(V_{\rm{re}}^{p}+{\rm{j}}V_{\rm{im}}^{p})(I_{\rm{re}}^{p}-{\rm{j}}I_{\rm{im}}^{p}) \right ]=Q_{\rm{sp}}=-\frac{V_{\rm{grid}}^{1}}{k_{\rm{q}}}-\frac{V_{\rm{ref}}^{1}}{k_{\rm{q}}}+Q_{\rm{ref}} \end{eqnarray}\]式中:\(Q_{\rm{ref}} 和 V_{\rm{ref}}^{1}\)为下垂控制器参考值;\(k_{\rm{q}}\)为下垂斜率;\(V_{\rm{grid}}^{1}\)并网口正序电压幅值。
PQ(V)节点不平衡分量控制方程和PV节点一样。
此外,当某相电流超过额定值时,需要将电压或无功约束方程切换至电流幅值约束(\(p\)为发生越限的序):
\[\begin{eqnarray} \label{eps11.20} \sqrt{(I_{\rm{re}}^{p})^{2}+(I_{\rm{im}}^{p})^{2}}=I_{\rm{lim}} \end{eqnarray}\]元件级建模
元件级建模方法是对元件进行机理研究、测量辨识或仿真拟合等方法建模后,用元件组建系统以描述整个系统的数学模型的方法。在分析分布式电源自身控制策略等各元件相互作用机理时,元件级建模能够获得系统级建模无法描述的内部特性。
本小节将简单介绍微型燃气轮机、风机系统、光伏发电并网系统、蓄电池储能系统的元件级模型。
微型燃气轮机
微型燃气轮机主要分为单轴结构和分轴结构两种。
单轴结构微型燃气轮机的压气机与发电机安装在同一转动轴上,分轴结构微型燃气轮机与单轴结构最大不同在于系统燃气涡轮与动力涡轮分别采用不同转轴。
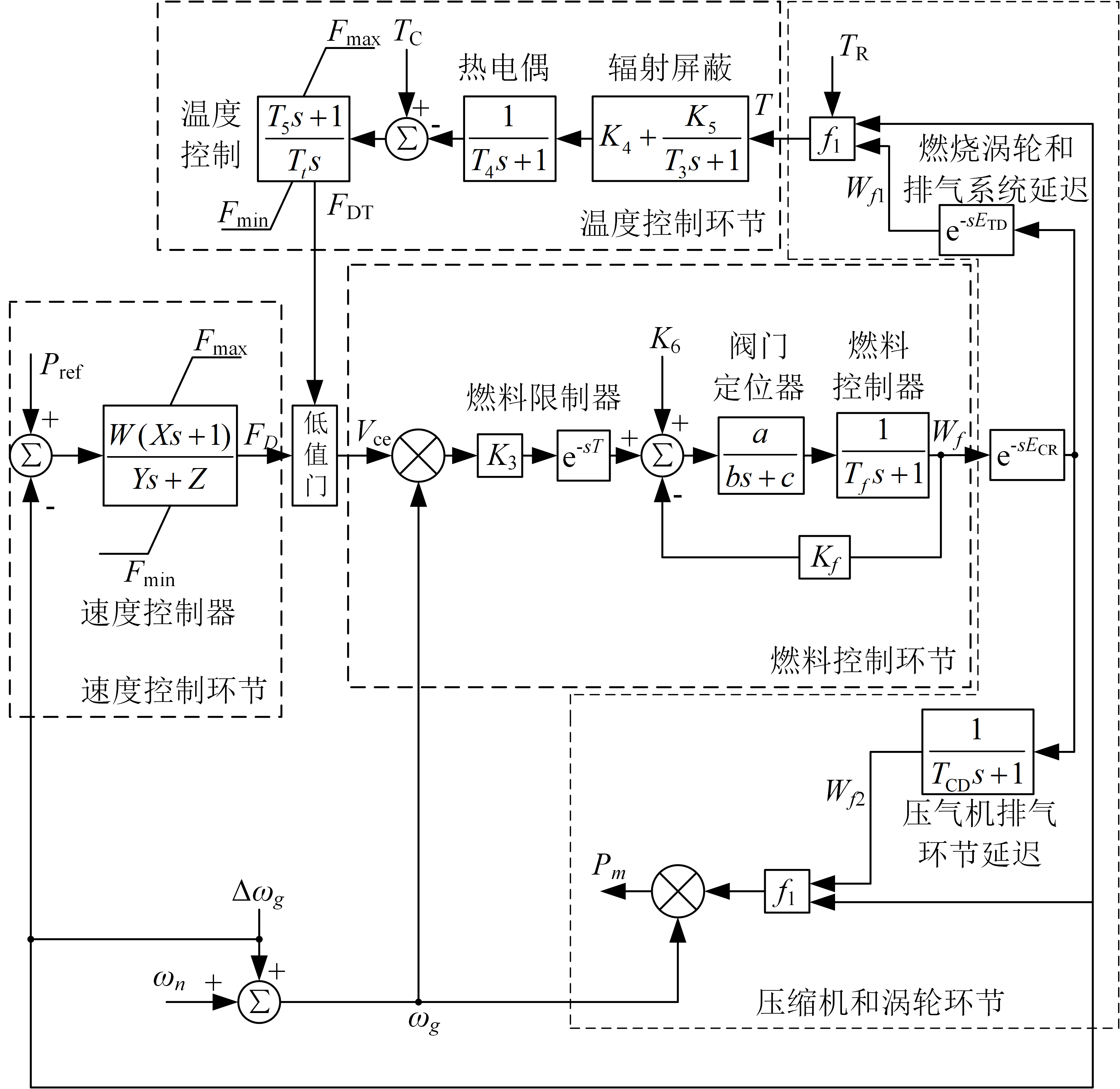
单轴结构微型燃气轮机
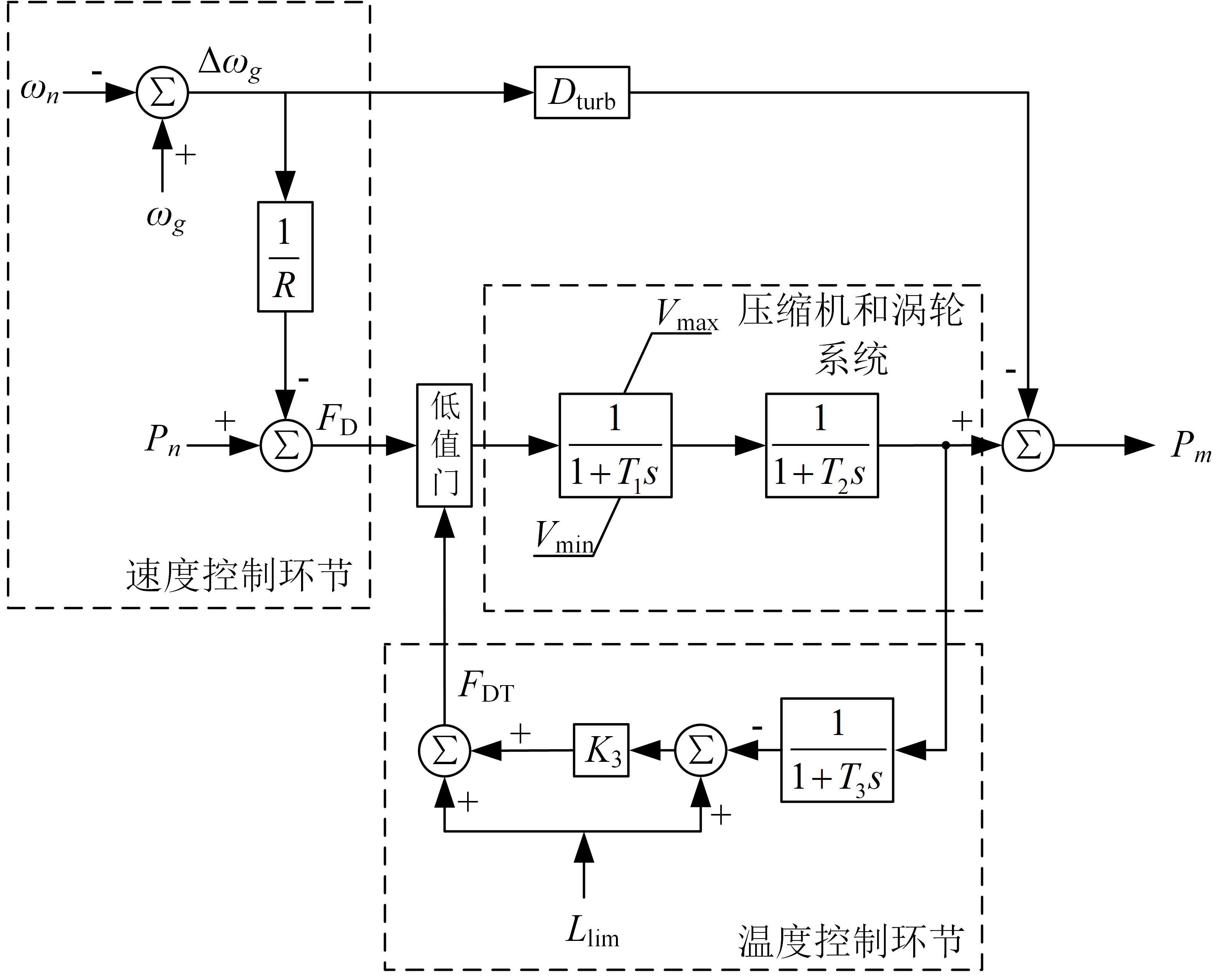
这里我们以Rowen微型燃气轮机仿真模型为例,其传递函数框图如下图所示。该模型主要由温度控制系统、速度控制系统、燃料系统和压缩机与涡轮系统组成。
分轴结构型微型燃气轮机
分轴结构微型燃气轮机原动系统由压气机、燃气涡轮、动力涡轮、燃烧室、回热器等组成。对内部进行适当简化,其模型可以由速度控制环节、温度控制环节、压缩机涡轮系统三部分表示。分轴结构微型燃气轮机的传递函数框图如下所示。
风机系统
分类:
按照发电机的类型划分,可分为同步发电机型和异步发电机型
按照风机驱动发电机的方式划分,可分为直驱式和使用增速齿轮箱驱动式
根据风速变化时发电机转速是否变化,将其分为恒频/恒速和恒频/变速两种
本节我们以恒频/恒速风力发电系统为例进行介绍。对于恒频恒速风机模型,仿真子系统包括空气动力系统模型、桨距控制模型、发电机轴系模型等。
空气动力系统模型
该模型描述将风能转化为风机功率输出的过程,能量转换公式为
\[\begin{eqnarray} \label{add10.3} P_{\rm{w}}=\frac{1}{2} \rho \pi R^{2} v^{3} C_{\rm{p}} \end{eqnarray}\]式中:\(C_{\rm{P}}\)为风能转换效率,是叶尖速比\(\lambda\)和叶片桨距角\(\theta\)的函数,表达式为
\[\begin{eqnarray} \label{add10.4} C_{\rm{p}}=f(\theta,\lambda) \end{eqnarray}\]叶尖速比\(\lambda\)定义为
\[\begin{eqnarray} \label{add10.5} \lambda =\frac{\omega _{\rm{w}} R}{V} \end{eqnarray}\]式中:\(\omega _{\rm{w}}\)为风机机械角速度 (rad/s)。
恒频/恒速变桨距控制的风力发电机组的一种\(C_{\rm{p}}\)特性曲线近似式为
\[\begin{eqnarray} \label{add10.6} C_{\rm{p}}=0.5( \frac{RC_{f}}{\lambda}-0.022\theta-2)e^{-0.255\frac{RC_{f}}{\lambda}} \end{eqnarray}\]式中:\(C_{f}\)为叶片设计参数,一般取1~3。
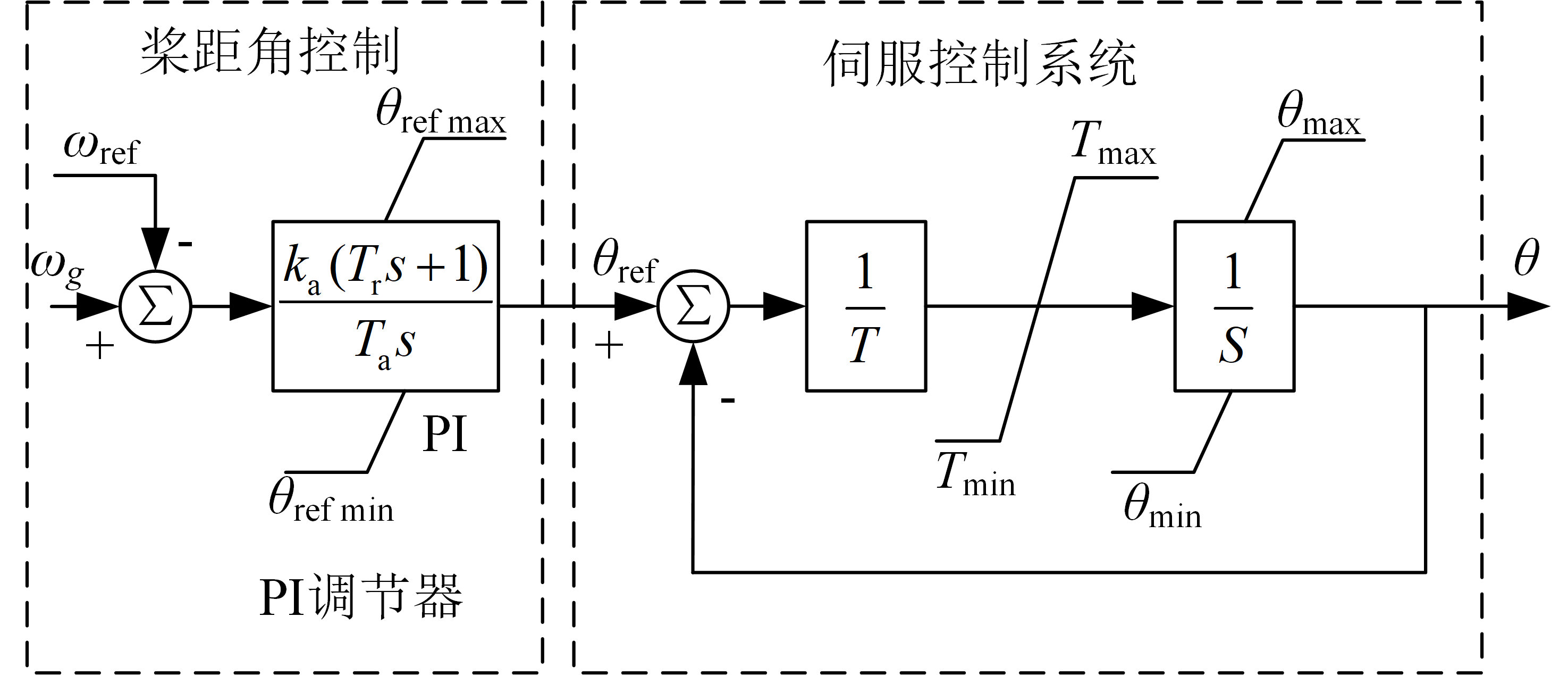
桨距控制模型
低压配电系统一般接入恒频恒速风力发电系统,以定桨距(主动失速型)风力发电机组为主导机型。
主动失速控制是指当风速在额定风速以下,控制器将桨距角置于\(0^{\circ}\),不做变化,可认为等同于定桨距风力发电机组,发电机的功率根据叶片的气动性能随风速的变化而变化。
下图是主动失速变桨距控制系统框图。
轴系模型
风力发电系统的轴系一般包含有三个质块:风机质块、齿轮箱质块和发电机质块。在建模中三质块模型、两质块模型和单质块模型都可能会涉及。
齿轮箱的惯性相比风机和发电机而言较小,当忽略齿轮箱惯性,将低速轴各量折算到高速轴上,得到的动态方程为式:
\[\begin{equation} \label{add10.7} \left\{\begin{aligned} &T_{\rm{w}}=J_{\rm{w}} \frac{\text{d} \omega _{\rm{w}}}{\text{d}t} + D_{\rm{tg}}(\omega _{\rm{w}}-\omega _{\rm{g}}) +K_{\rm{tg}}(\theta _{\rm{w}} - \theta _{\rm{g}}) \ \ \ \ \ \ \ T_{\rm{w}}=\frac{P_{\rm{w}}}{\omega _{\rm{w}}} \\ &-T_{\rm{g}}=J_{\rm{g}} \frac{\text{d} \omega _{\rm{g}}}{\text{d}t} + D_{\rm{tg}}(\omega _{\rm{g}}-\omega _{\rm{w}}) +K_{\rm{tg}}(\theta _{\rm{g}} - \theta _{\rm{w}}) \ \ \ \ \ \ \ T_{\rm{g}}=\frac{P_{\rm{g}}}{\omega _{\rm{g}}} \end{aligned}\right. \end{equation}\]光伏发电并网系统
光伏发电是指利用半导体的光生伏打效应将光能转化为电能的技术。若要实现并网,还需将光伏发电系统输出的直流电经升压、逆变过程达到并网要求。
常用的光伏电池模型有:理想电路模型、单二极管模型和双二极管模型。
单二极管模型模拟了光伏电池的内部损耗,双二极管模型还增加了一个二极管来模拟空间电荷的扩散效应。
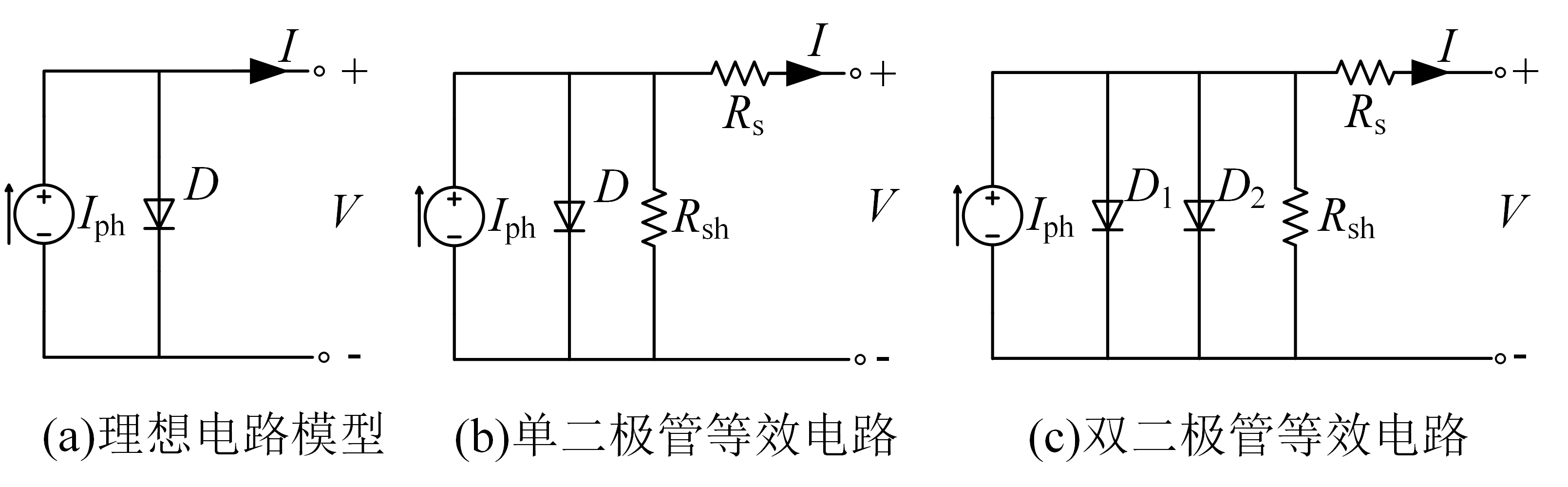
由双二极管模型给出的光伏电池输出伏安特性为
\[\begin{eqnarray} \label{add10.8} I=I_{\rm{ph}}-I_{\rm{s1}}(e^{\frac{q(V+IR_{\rm{s}})}{kT}}-1)-I_{\rm{s2}}(e^{\frac{q(V+IR_{\rm{s}})}{AkT}}-1)-\frac{V+IR_{\rm{s}}}{R_{\rm{sh}}} \end{eqnarray}\]当简化为单二极管模型时,相应的伏安关系为
\[\begin{eqnarray} \label{add10.9} I=I_{\rm{ph}}-I_{\rm{s}}(e^{\frac{q(V+IR_{\rm{s}})}{AkT}}-1)-\frac{V+IR_{\rm{s}}}{R_{\rm{sh}}} \end{eqnarray}\]以单二极管模型为例,当单一的光伏模块经过串、并联组成光伏阵列时,若假设光伏模块具有相同参数,则单二极管模型光伏阵列的输出电压和电流的关系如下:
\[\begin{eqnarray} \label{add10.10} I=N_{\rm{p}}I_{\rm{ph}}-N_{\rm{p}}I_{\rm{s}}(\text{e}^{\frac{q}{AkT}(\frac{V}{N_{\rm{s}}}+\frac{IR_{\rm{s}}}{N_{\rm{p}}})}-1)-\frac{N_{\rm{p}}}{R_{\rm{sh}}}(\frac{V}{N_{\rm{s}}}+\frac{IR_{\rm{s}}}{N_{\rm{p}}}) \end{eqnarray}\]式中:\(N_{\rm{s}}\)和\(N_{\rm{p}}\)分别为串联和并联的光伏电池数。
光伏电池的输出特性与光照幅度和环境温度相关,光照幅度和温度会影响到最大功率点电压。
最大功率点跟踪(Maximum Power Point Tracking,MPPT)就是要根据光伏电源的伏安特性,利用一些控制策略保证其工作在最大功率输出状态,可以最大限度地利用太阳能。目前,MPPT控制算法很多,如:扰动观测法,增量电导法,波动相关控制法,电流扫描法,模糊逻辑控制法,神经网络控制法等等。
蓄电池储能系统
蓄电池是一种电化学储能设备,既能够将氧化还原反应所释放出的化学能直接转变成低压直流电能,又能吸收电能转化为化学能储存,目前是分布式发电系统中应用最为广泛的储能设备之一。实际应用中,由于单个蓄电池的电压和容量往往不能满足需求,所以要将多个蓄电池串并联组成蓄电池组。
下面我们简单介绍两种蓄电池模型。
蓄电池简单等效模型
为了简化研究常常忽略蓄电池自身的充放电动态,用理想直流电压源或下图所示的简单等效电路作为蓄电池模型。
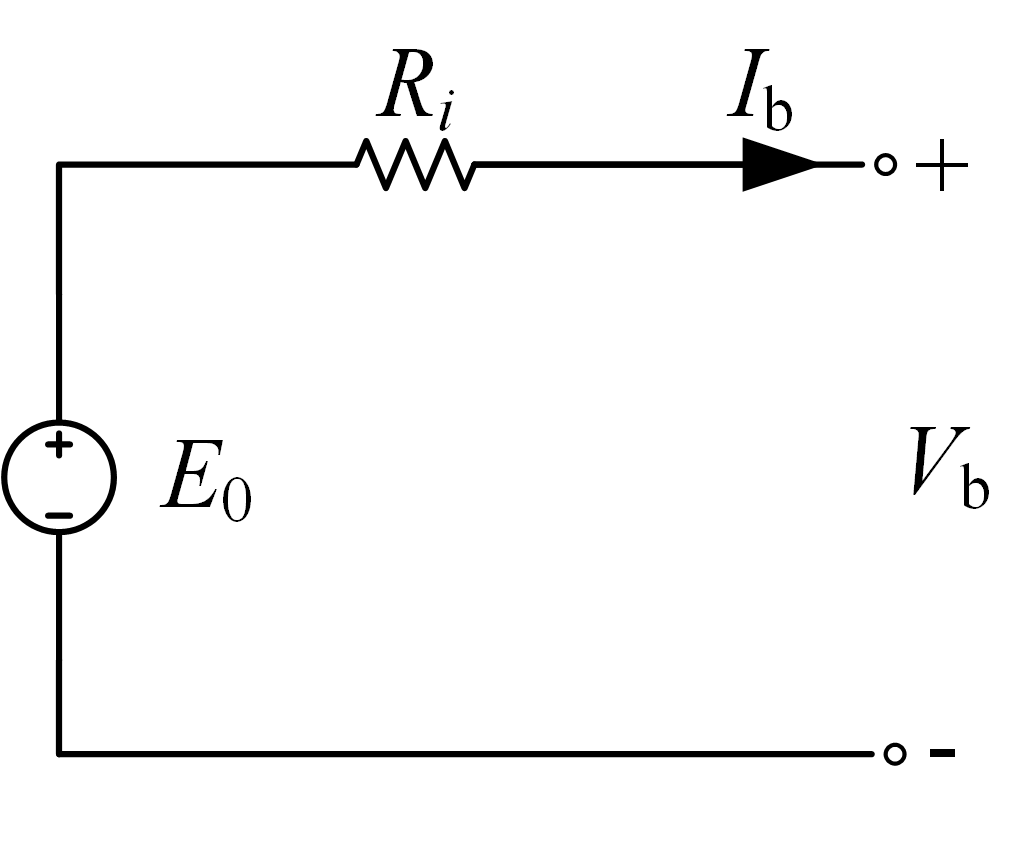
该等效电路由一个理想电压源串联电池内阻构成,特点是结构简单,参数恒定,适用于不考虑蓄电池动态特性的情况。该模型中,蓄电池端电压与流过蓄电池电流的关系如下式所示:
\[\begin{eqnarray} \label{add10.12} V_{\rm{b}}=E_{0}-I_{\rm{b}}R_{i} \end{eqnarray}\]式中\(E_{0}\)为理想电压源。
Thevenin等效电路模型
另外一种等效模型称之为Thevenin等效电路模型,由理想电压源\(E_{0}\),内阻\(R_{\rm{p}}\),过电压电容\(C_{0}\)和过压电阻\(R_{0}\)组成,如下图所示。
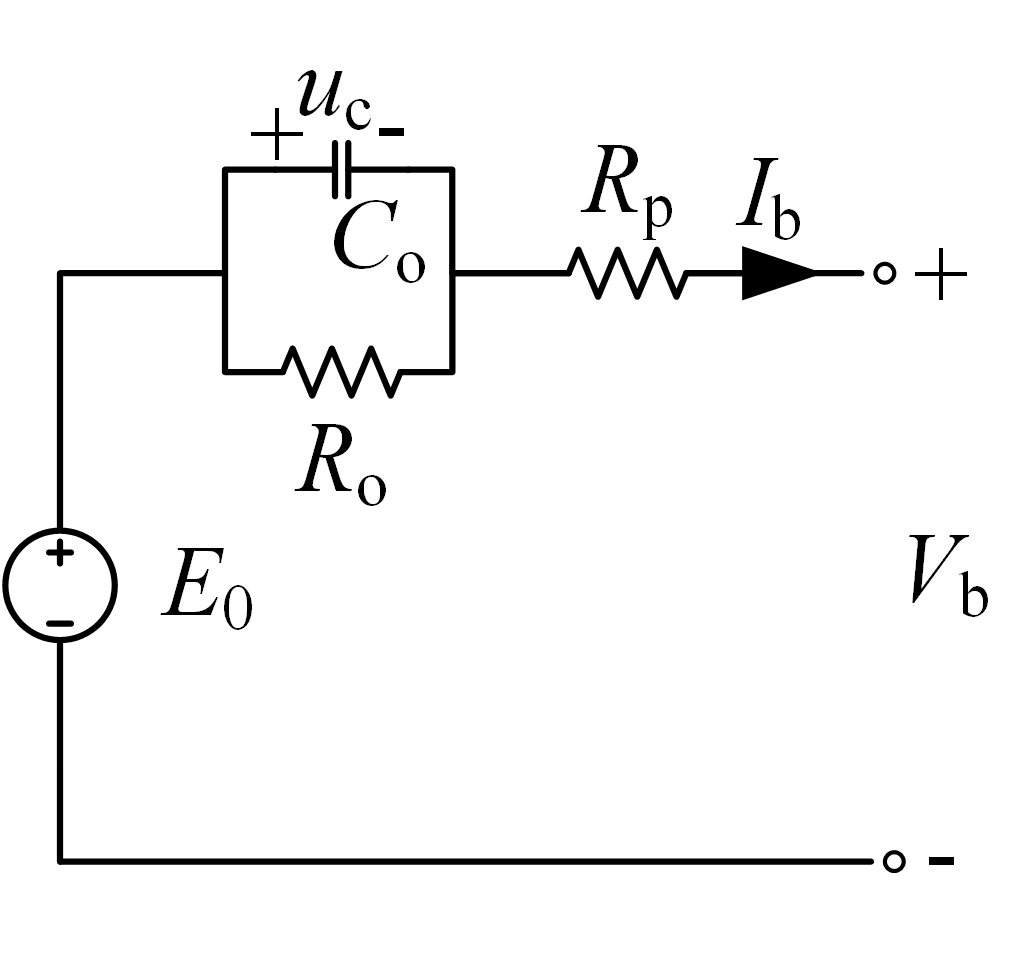
该等效电路模型可由下式描述
\[\begin{equation} \label{add10.13} \left\{\begin{aligned} &V_{\rm{b}}=E_{0}-u_{\rm{c}}-I_{\rm{b}}R_{i} \\ &\frac{\text{d}u_{\rm{c}}}{\text{d}t}=\frac{1}{R_{0}C_{0}}(I_{\rm{b}}R_{0}-u_{\rm{c}}) \end{aligned}\right. \end{equation}\]主动配电网分析
主动配电网的分析通常包括暂态分析、稳定性分析和潮流计算三部分。
暂态分析
暂态分析通过时域仿真手段对电力系统中各种快速变化的暂态过程进行详细模拟。
元件建模:暂态仿真能从元件的实际物理模型和系统结构出发,对包括电力电子设备、电网、分布式电源和各种控制器进行建模。
分析方法:应用电力系统电磁暂态仿真与电路仿真的基本理论和方法,模拟频率范围从几百千赫兹到工频之间系统中的电气量和非电气量的动态过程。
结果应用:应用其结果对智能配电网进行谐波分析、短路电流计算、负荷短时跟踪特性分析、故障特性分析、反孤岛保等多方面研究。
稳定性分析
电力系统稳定性的分类灵活多样,按时间长短可分为短期稳定、中期稳定和长期稳定;按照研究对象可分为功角稳定、频率稳定和电压稳定;按照所受扰动的大小可分为静态稳定和暂态稳定。
静态稳定性分析
静态稳定性分析也被称为小扰动分析,是电力系统遭受到较小扰动后,不发生非同期失步或自发振荡,自动恢复到初始运行状态的能力。
静态稳定性分析有多种方法,其中特征值法是静态稳定性分析方法中应用最广泛的一种。用特征值法分析主动配电网的步骤如下:
①确定控制方式,对和电网直接相连的逆变器或电动机进行线性化
②对电路网络进行线性化,得到系统的状态空间模型
③通过对状态方程进行计算得到的微电网稳定性特征值,分析该控制方式下的小信号稳定性。
暂态稳定性分析
暂态稳定性分析是在电力系统遭受到较大扰动后,对其能否恢复到原有运行状态或是达到新的稳定运行状态能力的分析。
按照对积分的依赖程度,现有的暂态稳定性分析方法可分为直接法、时域仿真法和混合法三类,其中,时域仿真法是暂态稳定性分析的基本方法。
含分布式电源的配电网的数学模型可以用高维非线性、非自治的分时段微分—代数方程组来描述,模型建立比较复杂。
潮流计算
分布式电源和微网的接入对配电网潮流、网损和电压分布有着重要影响,潮流计算是对其影响进行量化的直接手段。其潮流计算可分为配电网角度建模和分布式电源建模两种。
从配电网角度出发,潮流计算将从并网点处的分布式电源等效为一个节点,将各元件等效节点模型构成的系统非线性方程组进行求解即可得到在约束条件下的潮流分布。
分布式电源与配电网互联的接口可分为四种形式:同步发电机、异步发电机、电力电子换流器和双馈发电机。
从分布式电源的角度出发,含有分布式电源和微网的配电网潮流计算方法可以借鉴传统交直流混合电力系统的潮流求解方法。包括统一求解法和交替求解法。
微电网稳定性分析
为什么要进行微电网稳定性分析?
①微电网由于其内部元件的特殊性以及靠近用电负荷的特性,其结构与大电网相比更为脆弱。
②微电网在孤岛运行时,系统中没有根节点作为参考节点,更容易引起新的稳定性问题。
微电网稳定性分析主要包括动态稳定性、暂态稳定性和小干扰稳定性分析。
微电网动态稳定性
微电网动态稳定性分析主要用于预测参数发生改变时系统的动态行为,为控制参数的选择、微电网系统配置、运行控制策略的制定等提供理论依据和参考。
常见的分析方法有特征值分析法、辨识方法、频域分析法、奇异摄动法和动态向量法等。
微电网暂态稳定性分析
目前微电网暂态稳定性分析主要采用时域仿真法和李雅普诺夫能量函数法。
时域仿真法是揭示微电网内部的非线性现象和暂态稳定问题有力工具,由于其直观性得到广泛应用。
基于李雅普诺夫方法的暂态稳定性分析在传统电力系统中得到广泛研究,但适用于微电网暂态稳定性分析的能量函数法仍没有很好地建立和应用。
微电网小干扰稳定性
小信号稳定性也称小干扰稳定性,是指系统遭受小扰动的情况下保持同步运行的能力。定义一个扰动为小扰动,是指扰动造成的影响非常小,在分析中可以对描述系统响应的方程进行线性化而不影响分析的精度。
小信号稳定性分析的方法有多种,如特征值分析法、数值仿真法、频域分析法及Prony分析法等,其中特征值分析法能够提供很多与系统稳定相关的重要信息并对其设计也有帮助。下面我们采用特征值法进行分析。
特征值分析法
特征值分析法的基本思路是:
①计算给定的稳定运行点处各变量的稳态值
②将描述系统的非线性微分方程在稳定运行点处线性化,得到系统的线性化微分方程
③求出系统线性化微分方程的状态矩阵及其特征值,由特征值分析系统受到扰动后能否保持稳定
状态空间表示法
电力系统这样的动态系统,其行为可以用一组\(n\)个一阶非线性常微分方程描述
\[\begin{eqnarray} \label{wdw10.1} \dot{x_{i}}=f_{i}(x_{1},x_{2},\cdots,x_{n};u_{1},u_{2},\cdots,u_{r};t) \end{eqnarray}\]式中:\(n\)为系统的阶数;\(r\)为系统输入量的个数。
\[\begin{eqnarray} \label{wdw10.2} \dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x},\boldsymbol{u},t) \end{eqnarray}\]向量\(\boldsymbol{x}\)为状态向量,它的每个元素为状态变量;
向量\(\boldsymbol{u}\)为系统的输入向量,是影响系统行为的外部信号;
\(t\)表示时间,状态变量对时间的导数用微分\(\dot{\boldsymbol{x}}\)来表示。
状态空间表示法(续)
若系统状态变量的导数并不是时间的显函数,则称其为自治系统。此时,上式可简化为
\[\begin{eqnarray} \label{wdw10.3} \dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x},\boldsymbol{u}) \end{eqnarray}\]输出变量可用状态变量及输入变量表示成如下形式
\[\begin{eqnarray} \label{wdw10.4} \boldsymbol{y}=\boldsymbol{g}(\boldsymbol{x},\boldsymbol{u}) \end{eqnarray}\]其中:
\[ \boldsymbol{y}=\begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{bmatrix} \quad \boldsymbol{g}=\begin{bmatrix} g_{1} \\ g_{2} \\ \vdots \\ g_{m} \end{bmatrix} \]
向量\(\boldsymbol{y}\)为输出向量,向量\(\boldsymbol{g}\)是将状态变量、输入变量与输出变量联系起来的非线性函数向量。
方程线性化
在小信号稳定性分析中,通常认为电力系统因小的负荷变化或发电变化而产生的扰动足够小,可以将系统的非线性微分方程在初始稳定运行点处进行线性化,得到近似的线性状态方程。
对于公式\(\dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x},\boldsymbol{u})\),令\(\boldsymbol{x}_{0}\)代表稳定运行时的状态向量,\(\boldsymbol{u}_{0}\)对应于稳定运行时的输入向量,那么有
\[\begin{eqnarray} \label{wdw10.6} \dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x_{0}},\boldsymbol{u_{0}}) \end{eqnarray}\]对系统的上述状态施加一个小扰动,则有
\[\begin{eqnarray} \label{wdw10.7} \boldsymbol{x}=\boldsymbol{x_{0}}+\Delta \boldsymbol{x}, \quad \boldsymbol{u}=\boldsymbol{u_{0}}+\Delta \boldsymbol{u} \end{eqnarray}\]新状态也必须满足上式,因此
\[ \dot{\boldsymbol{x}}=\dot{\boldsymbol{x_{0}}}+\Delta \dot{\boldsymbol{x}}=\boldsymbol{f}[(\boldsymbol{x_{0}}+\Delta \boldsymbol{x}),(\boldsymbol{u_{0}}+\Delta \boldsymbol{u})] \]
非线性函数\(\boldsymbol{f}(\boldsymbol{x},\boldsymbol{u})\)用泰勒级数展开,当忽略\(\Delta \boldsymbol{x}\)和\(\Delta \boldsymbol{u}\)的二阶和二阶以上的高阶项时,可得
\[\begin{equation} \label{wdw10.8} \begin{split} \dot{x_{i}}&=\dot{x_{i0}}+\Delta \dot{x_{i}}=f_{i}[(\boldsymbol{x_{0}}+\Delta \boldsymbol{x}),(\boldsymbol{u_{0}}+\Delta \boldsymbol{u})]\\ &=f_{i}(\boldsymbol{x}_{0},\boldsymbol{u}_{0})+\frac{\partial f_{i}}{\partial x_{1}} \Delta x_{1} + \cdots +\frac{\partial f_{i}}{\partial x_{n}} \Delta x_{n} + \frac{\partial f_{i}}{\partial u_{1}} \Delta u_{1} + \frac{\partial f_{i}}{\partial u_{r}} \Delta u_{r} \end{split} \end{equation}\]即
\[\begin{eqnarray} \label{wdw10.9} \Delta \dot{x_{i}}=\frac{\partial f_{i}}{\partial x_{1}} \Delta x_{1} + \cdots +\frac{\partial f_{i}}{\partial x_{n}} \Delta x_{n} + \frac{\partial f_{i}}{\partial u_{1}} \Delta u_{1} + \frac{\partial f_{i}}{\partial u_{r}} \Delta u_{r} \end{eqnarray}\]式中:\(i=1,2,\cdots,n\)。
同理有
\[\begin{eqnarray} \label{wdw10.10} \Delta \dot{y_{j}}=\frac{\partial g_{j}}{\partial x_{1}} \Delta x_{1} + \cdots +\frac{\partial g_{j}}{\partial x_{n}} \Delta x_{n} + \frac{\partial g_{j}}{\partial u_{1}} \Delta u_{1} + \frac{\partial g_{j}}{\partial u_{r}} \Delta u_{r} \end{eqnarray}\]式中:\(j=1,2,\cdots,n\)。
得到线性化形式为
\[\begin{equation} \label{wdw10.11} \left\{\begin{aligned} \Delta \dot{\boldsymbol{x}}=\boldsymbol{A} \Delta \boldsymbol{x}+\boldsymbol{B} \Delta \boldsymbol{u} \\ \Delta \boldsymbol{y}=\boldsymbol{C} \Delta \boldsymbol{x}+\boldsymbol{D} \Delta \boldsymbol{u} \end{aligned}\right. \end{equation}\]上述偏微分方程是在所分析的小扰动的初始稳定运行点基础上推导得到的。 其中:
\(\Delta \boldsymbol{x}\)是\(n\)维状态向量
\(\Delta \boldsymbol{u}\)是\(r\)维输入向量
\(\Delta \boldsymbol{y}\)是\(m\)维输出向量
\(\boldsymbol{A}\)为\(n×n\)阶的状态矩阵
\(\boldsymbol{B}\)为\(n×r\)阶的控制或输入矩阵
\(\boldsymbol{C}\)为\(m×n\)为阶的输出矩阵
\(\boldsymbol{D}\)为\(m×r\)阶的前馈矩阵,定义了直接出现于输出中的部分输入。
特征值与稳定性
下图是状态空间框图,初始状态\(\Delta \boldsymbol{x}(0)\)假定为零。
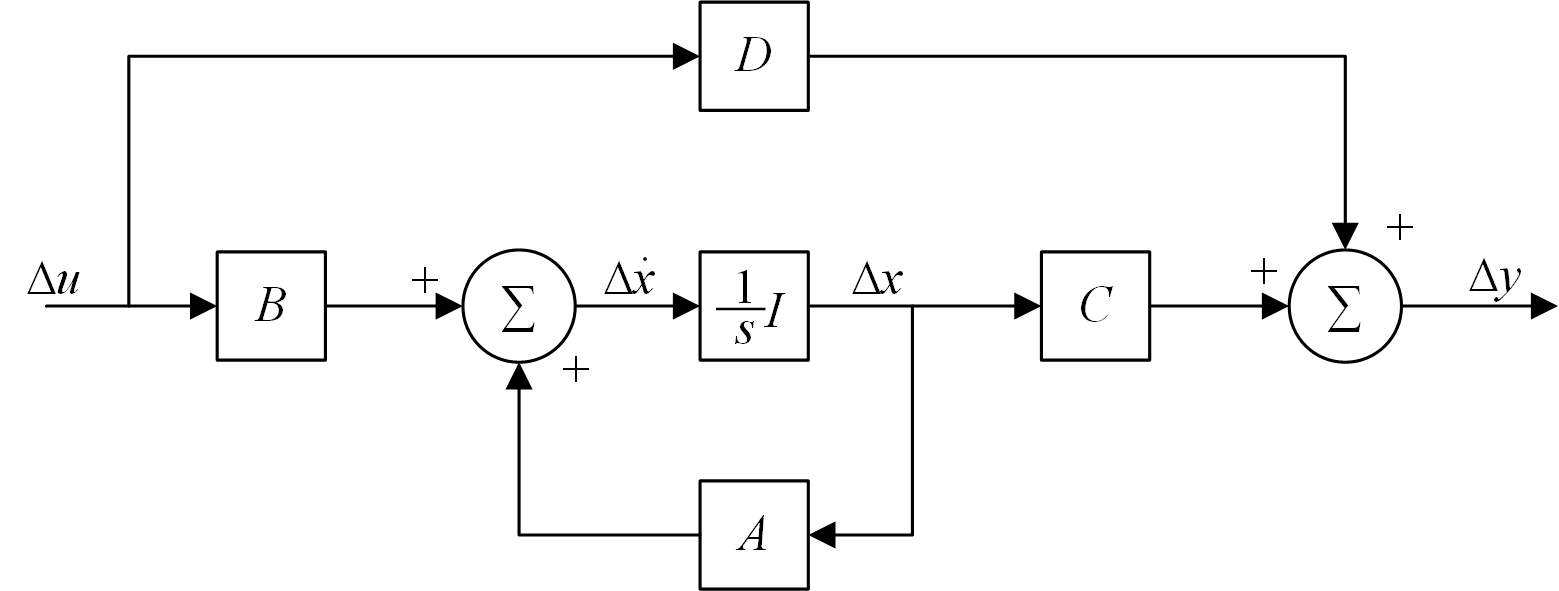
对刚刚得到的线性化方程做拉氏变换,在频域上状态等式为
\[\begin{equation} \label{wdw10.12} \left\{\begin{aligned} &s\Delta \boldsymbol{x}(s)-\Delta \boldsymbol{x}(0)=\boldsymbol{A} \Delta \boldsymbol{x}(s)+\boldsymbol{B} \Delta \boldsymbol{u}(s) \\ &\Delta \boldsymbol{y}(s)=\boldsymbol{C} \Delta \boldsymbol{x}(s)+\boldsymbol{D} \Delta \boldsymbol{u}(s) \end{aligned}\right. \end{equation}\]求解\(\Delta \boldsymbol{x}(s)\)和\(\Delta \boldsymbol{y}(s)\)可得状态方程的解,整理上式有
\[\begin{eqnarray} \label{wdw10.13} (s\boldsymbol{I}-\boldsymbol{A})\Delta \boldsymbol{x}(s)=\Delta \boldsymbol{x}(0)+\boldsymbol{B}\Delta \boldsymbol{u}(s) \end{eqnarray}\]因而
\[\begin{eqnarray} \label{wdw10.14} \Delta \boldsymbol{x}(s)=(s\boldsymbol{I}-\boldsymbol{A})^{-1}[\Delta \boldsymbol{x}(0)+\boldsymbol{B}\Delta \boldsymbol{u}(s)]=\frac{\text{adj}(s\boldsymbol{I}-\boldsymbol{A})}{\text{det}(s\boldsymbol{I}-\boldsymbol{A})}[\Delta \boldsymbol{x}(0)+\boldsymbol{B}\Delta \boldsymbol{u}(s)] \end{eqnarray}\]同时有
\[\begin{eqnarray} \label{wdw10.15} \Delta \boldsymbol{y}(s)=\boldsymbol{C} \frac{\text{adj}(s\boldsymbol{I}-\boldsymbol{A})}{\text{det}(s\boldsymbol{I}-\boldsymbol{A})}[\Delta \boldsymbol{x}(0)+\boldsymbol{B}\Delta \boldsymbol{u}(s)] +\boldsymbol{D} \Delta \boldsymbol{u}(s) \end{eqnarray}\]\(\Delta \boldsymbol{x}\)和\(\Delta \boldsymbol{y}\)的拉氏变换含有两个分量,分别取决于初始状态和输入。
\(\Delta \boldsymbol{x}(s)\)和\(\Delta \boldsymbol{y}(s)\)的极点是下式的根
\[\begin{eqnarray} \label{wdw10.16} \text{det}(s\boldsymbol{I}-\boldsymbol{A})=0 \end{eqnarray}\]满足上式的值称为矩阵的特征值,该式称为矩阵\(\boldsymbol{A}\)的特征方程。
非线性系统的稳定性
非线性系统的稳定性通常根据状态向量在状态空间的区域大小划分为如下几种情况:
①局部稳定
当系统遭受小扰动后,若仍能回到平衡点周围的小区域内,则说明系统在此平衡点处是局部稳定的。
②有限稳定
当系统遭受小扰动后,若其状态保持在一个有限的区域R内,则说明系统在区域R内是稳定的。
③全局稳定(大范围稳定)
如果区域包括整个有限空间,则系统是全局稳定的。根据李雅普诺夫第一法,对于非线性系统,其小信号稳定性是由系统线性化后特征方程的根确定的:
1)当\(\boldsymbol{A}\)的所有特征值的实部均为负时,系统是渐进稳定的。
2)当\(\boldsymbol{A}\)的特征值中至少存在一个实部为正时,系统是不稳定的。
3)当\(\boldsymbol{A}\)至少有一个特征值实部为零,而其他特征值实部均为负时,系统为临界稳定状态。